Теплопередача через однослойную и многослойную цилиндрические стенки

До

0_

а_хР ЯР

(2.193)

и

= 1

^О^Р

с2~'2*

Складывая почленно левые и правые части уравнений системы (2.193), получим уравнение теплопередачи через однослойную плоскую стенку

Я

(2.194)

1 5 1

— + - + —

а

X а₂

В уравнении (2.194) величина 1/(1/а! + ёГк + 1/а₂) обозначается буквой к, измеряется в
Вт/(м^К) и называется коэффициентом теплопередачи: Р

к =

1 3 1

— + - + —

«1 I «2

Тогда уравнение (2.194) можно будет записать в следующем виде:

() = кР({₁-{₂).

(2.195)

(2.196)

Числовое значение коэффициента теплопередачи выражает количество теплоты, проходящей через единицу поверхности стенки в единицу времени от горячего к холодному теплоносителю при разности температур между ними в 1 °.

Полученное уравнение (2.196) называют уравнением теплопередачи. Для определения к требуются предварительные определения й1 и а₂, которые в большинстве случаев являются величинами сложными, поскольку учитывают передачу теплоты за счет нескольких видов теплообмена.

Значение к всегда меньше наименьшего значения коэффициента теплоотдачи а. Величина, обратная коэффициенту теплопередачи, называется полным термическим сопротивлением через однослойную плоскую стенку, обозначается буквой К, (м²-К)/Вт

_ 1 1 3 1

а

;? = _ = —+-+_.

(2.197)

Здесь 1/«1 и \1а₂ - внешние термические сопротивления теплоотдачи; д/Х - внутреннее термическое сопротивление стенки.

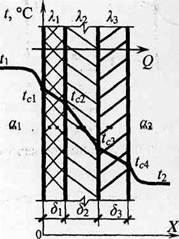
В случае передачи теплоты через многослойную плоскую стенку (рис. 2.52) в знаменателе формулы (2.194) нужно поставить сумму термических сопротивлений всех слоев

2 =

(2.198)

«1 1-14 «2

Коэффициент теплопередачи к, Вт/(м²-К), через многослойную плоскую стенку равен

к =

(2.199)

Рис. 2.52. Теплопередача через Полное термическое сопротивление К, (м²-К)/Вт, трехслойную плоскую стенку через многослойную плоскую стенку равно

к Й! /=1^- а₂

(2.200)

Температура на поверхностях плоской стенки определяется из следующих уравнений:

*о\^шЧ-

(2.201)

*с*='г +

а₂Р

(2.202)

При известных а\, а₂п к температуры поверхностей плоской стенки можно найти по формулам

>_С1='1--('1-'2)" ^; (²-²⁰³)

«1

^4^е^+-

.₂-г~(/,^). (2-204)

«2

Предположим, что через цилиндрическую однородную стенку переносится теплота при
стационарном режиме от горячего теплоносителя с постоянной температурой 1\ и
коэффициентом теплоотдачи а,\ к холодному теплоносителю с постоянной температурой 1₂ и
коэффициентом теплоотдачи а₂ (рис. 2.53). ^

Тогда для теплового потока можно написать три уравнения:

(2.205)

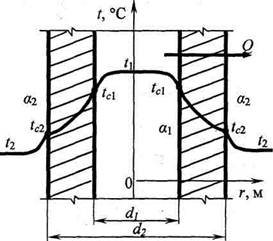
Рис. 2.53. Теплопередача через однослойную цилиндрическую стенку

<

й

—1п—

2Х а_х

д=а_г7са₂!({_с2-(₂).

Здесь / - высота цилиндрической стенки, м; X -коэффициент теплопроводности стенки, Вт/(м-°С). Решая эти уравнения относительно разности температур, а затем складывая, получим уравнение теплопередачи через однослойную цилиндрическую стенку

(2.206)

^=

**('1-'2)

1, <*2 ■ + — 1п ¹

а^1 21 с1\ о.₂а¹₂

+ ■

Уравнение (2.206) можно написать в следующем виде:

0, = Ъ_чжЩ_х-1_г).

Здесь величину кц называют линейным коэффициентом теплопередачи, Вт/(м-К). Линейный коэффициент теплопередачи кц находится по формуле

(2.207)

** =

1, ^2 +—1п- --

+ -

2«₂

*1^М1

а,^, 2Х д_Л о^а¹-

(2.208)

Числовое значение линейного коэффициента теплопередачи цилиндрической стенки к_ц есть количество теплоты, проходящей через 1 м трубы в единицу времени от горячего теплоносителя к холодному при разности температур между ними в 1 °.

Значения плотности теплового потока #1 и а₂, Вт/м², отнесенные к внутренней или наружной поверхности, будут отличны друг от друга и равны соответственно

(2.209)

д₂ =

_ ч

па¹ 4 а¹-,

Ц\-ЧУ

(2.210)

Величину, обратную линейному коэффициенту теплопередачи, обозначают К_ц, м-К/Вт, и называют полным линейным термическим сопротивлением теплопередачи через цилиндрическую стенку

Я ₌± ₌ _1_ ₊ ±1_п^. ₊ _1_, (2.211)

к_ц а_хЛ_х 2Х 4_Х а₂й?₂

1 1 '1 //

где ----- и —— - термические сопротивления теплоотдачи; —-1п— - термическое

а_хс1_х а₂с1₂ 2Х Л_х

сопротивление однослойной цилиндрической стенки.

Температуры внутренней и наружной поверхностей цилиндрической стенки 1_сХ и 1_Л, °С, определяются по формулам

'с1^в'1Нг7* - ^¹²⁾

^2=^2-Ь-4-7- (2-213)

При переносе теплоты через многослойную цилиндрическую стенку, имеющую п слоев, тепловой поток <2, Вт, будет равен

п = _________ л1{1_х-^) (2.214)

--- + 2—1п-^ш- +-------

2.6.4. Критический диаметр изоляции

Тепловой изоляцией называют всякое покрытие горячей поверхности, которое способствует снижению потерь теплоты в окружающую среду. Для тепловой изоляции могут быть использованы любые материалы с низкой теплопроводностью - пробка, минеральная вата, пенополиуретан, пенополистирол и другие, но теплоизоляционными считаются только те материалы, коэффициент теплопроводности которых X < 0,2 Вт/(м-°С).

Анализ формулы полного линейного термического сопротивления теплопередачи цилиндрической стенки показывает, что тепловые потери изолированных трубопроводов уменьшаются не пропорционально увеличению толщины изоляции.

Рассмотрим условие, при котором материал, используемый для изоляции трубы, будет уменьшать тепловые потери.

Пусть цилиндрическая труба покрыта однослойной изоляцией. При постоянных а_х, а₂, А\, <%₂, Х\, Х₂, 1\ и (% рассмотрим, как будет изменяться полное термическое сопротивление при изменении толщины изоляции.

Уравнение полного термического сопротивления двухслойной цилиндрической стенки имеет вид

' *.Х.^ ₊ Хы4 ₊ Хь^ + -и (2215)

к_ц о._хс1_х 2Х_Х Л_х 2Х₂ а?₂ «г^з

где й?з ^- наружный диаметр изоляции, м; Х₂ - коэффициент теплопроводности изоляции, Вт/(м-К).

При увеличении внешнего диаметра изоляции ^ увеличивается сопротивление слоя

на

изоляции

1п^1, но одновременно уменьшается сопротивление теплоотдачи '

2^2 <*2 1 \^2^*3 /

наружной поверхности изоляции.

Возьмем первую производную от правой части уравнения (2.215) по */₃ и приравняем ее к нулю, в результате получим

<*(4») ₌ 1____ 1_

^(^з) ²^2^3 «2^3

= 0-

(2.216)

Тогда критический диаметр изоляции йщ, отвечающий экстремальной точке кривой функции К_ц =Х^з)₅ определяется формулой

(2.217)

2^

а->

"■кр ^из

Из уравнения (2.217) следует, что критический диаметр изоляции не зависит от размеров трубопровода. Он будет тем меньше, чем меньше коэффициент теплопроводности изоляции и чем больше коэффициент теплоотдачи аг от наружной поверхности изоляции к окружающей среде.

Вторая производная от К_ц больше нуля. Следовательно, критический диаметр соответствует минимуму теплового сопротивления и максимуму теплового потока (рис. 2.54).

Анализ уравнения (2.217) показывает, что если наружный диаметр изоляции 4_Ю увеличивается, но остается меньше йщ,, то тепловые потери возрастают и будут больше теплопотерь голого трубопровода (кривая АК). При равенстве 4_Ю - дщ, получаются максимальные теплопотери в окружающую среду (точка К). При дальнейшем увеличении наружного диаметра изоляции </_ю ^> ^кр теплопотери будут меньше, чем при й_т = йщ, (кривая ВК).

К а_ш > а_т

⁹т4

Только при а\з = ^з тепловые потери вновь станут такими же, как и для неизолированного трубопровода.

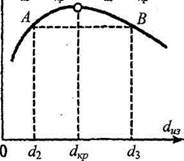Значит, для эффективной работы изоляции необходимо, чтобы критический диаметр был меньше внешнего диаметра оголенного трубопровода, т. е. чтобы 4кр - ^2 (рис. 2.54). Таким образом, для того чтобы изоляция вызвала уменьшение теплопотерь цилиндрической стенки по сравнению с голым трубопроводом, при данном наружном диаметре трубы й?2 и заданном коэффициенте теплоотдачи а₂, необходимо, чтобы

«2^2

(2.218)

Х_из<-

Рис. 2.54. Зависимость тепловых
потерь от диаметра изоляции ^А

Например, для изоляции трубопровода диаметром й?₂ ⁼ 30 мм имеется шлаковая вата, теплопроводность которой Х_ю = 0,1 Вт/(м-К), коэффициент теплоотдачи аг = 4,0 Вт/^-К). Целесообразно ли применять в данном случае в качестве изоляции шлаковую вату?

Критический диаметр изоляции 4ср ⁼ 2Я_Ю / аг = 2 • 0,1/ 4 = 0,05 м = 50 мм. Так как й_т > йг, шлаковую вату в рассматриваемом случае применять нецелесообразно. Для нашей задачи Х_ш должна быть меньше, т. е. Х_ш < 4 • 0,03/ 2 = 0,06 Вт/(м-К).

Дата добавления: 2014-01-04