Лекция 2. Расчет переходных процессов в цепях с одним накопителем энергии

Классический метод расчета переходных процессов

Аналитический расчет переходных процессов сводится в конечном счете к нахождению общих интегралов обычных линейных дифференциальных урав-нений с постоянными коэффициентами. Порядок дифференциального урав-нения, описывающего соотношение токов и напряжений в электрической це- пи при переходном режиме, определяется числом мест накопления в данной цепи энергии электрического или магнитного поля. Известно, что ток в кон-денсаторе 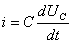. Если этот же ток протекает по катушке индуктивности, то напряжение на ней 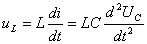и т.д.

В общем случае, если в цепи имеется n мест накопления энергии, уравнение может принять вид:

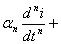
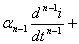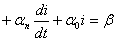
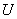… (1.1)

Общий интеграл дифференциального уравнения с правой частью представляет собой сумму частного решения этого уравнения и решения того же уравнения без правой части, т.е. общего решения.

Общее решение физически определяет электромагнитные процессы, про-исходящие в цепи при отсутствии внешних источников энергии, за счет того запаса энергии, который был в начальный момент времени в электрическом и магнитном полях, связанных с цепью. Но в реальных цепях всегда имеет мес-

то рассеяние энергии (на нагрев проводов и сопротивлений) и ее выделение в виде тепла. Таким образом, токи и напряжения, определяемые из линейных дифференциальных уравнений без правой части, с течением времени стремятся к нулю. Эти составляющие по своему характеру не зависят от внешних источников энергии и поэтому называются свободными составляющими.

Общий вид свободной составляющей, например, тока, найденной из уравнения (1):

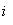_св. = 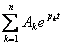, (1.2)

где 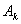– постоянная интегрирования, найденная из начальных условий. Начальные условия – это значения при 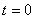величин, которые не могут меняться скачком, т.е. ;

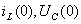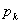– корни характеристического уравнения.

Применительно к уравнению (1.1) характеристическое уравнение будет иметь вид: 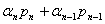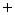…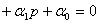. (1.3)

Число корней равно порядку дифференциального уравнения. В общем

случае корни могут быть комплексными числами, вещественная часть которых всегда отрицательна

,

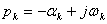где характеризует скорость затухания экспоненты и называется коэффициентом затухания.

Постоянная времени .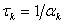

Мнимую часть корня 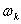называют угловой частотой собственных колебаний.

Частное решение дает значение тока, напряжения при 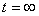, т.е. при установившемся режиме. Характер и величина этой составляющей определяется внешними источниками энергии, поэтому она называется принужденной составляющей.

Например, если в (1.1) напряжение 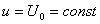, то и принужденный ток

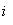_пр. 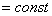и не зависит от времени. Тогда все производные обратятся в ноль и получим _пр. .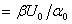

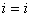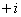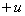Итоговое значение тока определяется как сумма общего и частного решений: _{св. пр.} . Если искомым является напряжение, то _св.пр. .

Таким образом, решение свелось к методу наложения: определяя частное решение (_пр.) полагают, что действуют только внешние источники энергии. Определяя свободные составляющие, наоборот, приравнивают нулю внешние источники и учитывают действие только внутренних сил, обусловленных накопленной в цепи энергией. Необходимо помнить, что реально существуют только действительные токи и напряжения, а их разложение на принужденные

и свободные составляющие – лишь прием, облегчающий расчет.

1.3. Включение цепи на постоянное напряжение (рисунок 1.1)

форме)

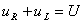или 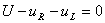_. (1.4)

Известно 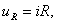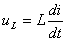. (1.5)

Подставим (1.5) в (1.4) 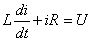, (1.6)

т.е. получили линейное дифференциальное уравнение первого порядка.

Находим частное решение (1.6), т.е. _пр.

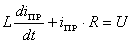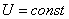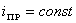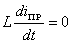. Так как , то , , а 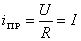. (1.7)

Получился ток установившегося режима, который был бы в цепи с пер-

вого момента замыкания ключа, если бы не возникающая в катушке ЭДС самоиндукции, которая противодействует изменению тока.

Общее решение, т.е. _св.

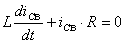. (1.8)

Решим (1.8) разделением переменных: .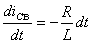

Интегрируя, получим 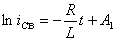. Постоянную 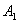можно определить

как 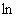некоторой другой постоянной 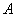, т.е. считать, что 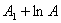. Тогда

,

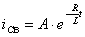где - корень характеристического уравнения 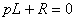, т.е. .

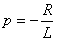Постоянная 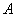находится из начальных условий: при 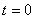ток в катушке равен нулю (по первому закону коммутации), т.е. 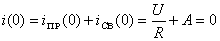. Отку-да 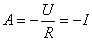и 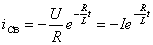. (1.9)

В последующем будем записывать _св. сразу в общем виде не приводя подробного решения, а пользуясь выражением _св. .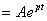

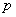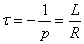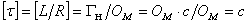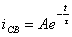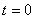
Так как корень – вещественный, то постоянная времени . Единица измерения . Используя можно записать . Физический смысл : при _св.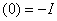, а при _cв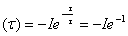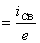, таким образом – это время, за которое свободная составляющая уменьшится в 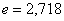... раз.

Действительное значение тока

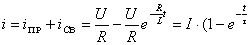
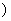(1.10)

На рисунке 1.2 приведен график :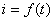

Цель лекции: усвоить классический метод расчета переходных процессов в простейших электрических цепях.

2.1 Короткое замыкание цепи с

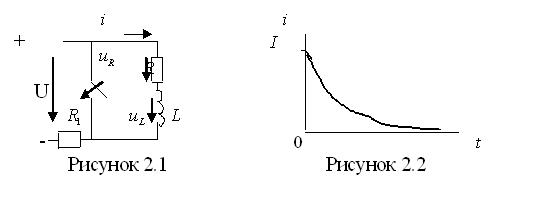
Пусть заданы значения 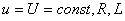. Определить .

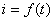Составляем уравнение замкнутого контура по второму закону Кирхгофа в дифференциальной форме:

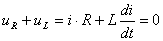. (2.1)

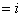Находим принужденную составляющую тока _пруст.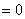 (переходный процесс в катушке не зависит от внешнего напряжения U). Следовательно 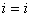_св.

Свободная составляющая тока из (2.1) _св .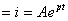

Характеристическое уравнение 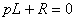, т.е.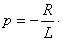

Постоянную интегрирования 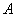определяем из начальных условий:

при 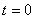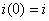_св..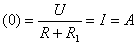

На рисунке 2.2 приведена кривая 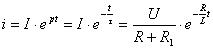. (2.2)

Проверим расход энергии. До начала переходного процесса в магнитном поле катушки была запасена энергия 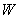_м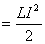. Энергия, перешедшая за время переходного процесса в тепловую

.

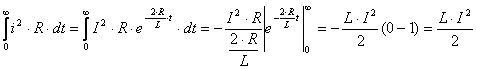Таким образом, весь запас энергии магнитного поля перешел в тепловую энергию в сопротивлении .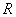

2.2 Включение цепи 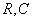на постоянное напряжение

Выражаем ток через 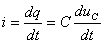. (2.4)

С учетом (2.4) уравнение электрического равновесия цепи запишем в виде

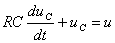, (2.5)

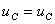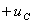где _{пр. св.}.

Определяем _{пр. пр.=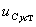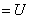} . (2.6)

Здесь ток будет протекать до тех пор, пока конденсатор не зарядится.

Так как уравнение (2.5) первого порядка, то свободная составляющая напряжения _св 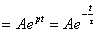. (2.7)

Характеристическое уравнение 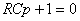, откуда .

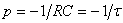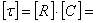Ом_.·Ф = Ом_.· Ом^.-1_.· с. = с.

Определяем постоянную интегрирования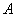

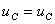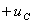_пр.св.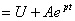. (2.8)

При 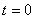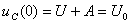, откуда А = U₀ – U, таким образом

_св. 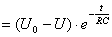. (2.9)

Итоговый результат: 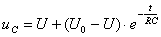. (2.10)

При .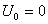

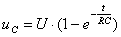Зарядный ток конденсатора: 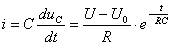(2.11)

При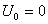 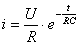. (2.12)

На рисунке 2.4 приведен примерный вид кривых 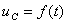и .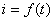

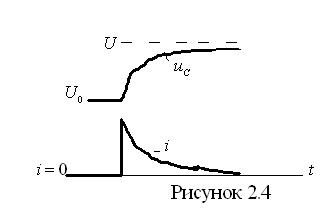
2.3 Включение цепи на синусоидальное напряжение

Пример такого переходного процесса – включение трансформатора в режиме холостого хода при малом насыщении сердечника.

Переходные процессы в цепях переменного тока сильно зависят от того, в какой момент, при каком мгновенном значении напряжения происходит включение цепи. Поэтому обязательно надо учитывать не только действую-щее значение или амплитуду напряжения сети, но и начальный фазовый угол в момент включения цепи.

Рассмотрим цепь рисунка 2.5.

Составляем уравнение электрического равновесия цепи

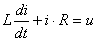. (2.13)

Принужденная составляющая тока _пр.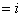уст. , но при установившемся

режиме ток определяется законом Ома

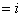_{пр. уст.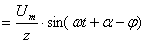} , (2.14)

где ;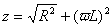

.

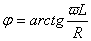В более сложных цепях ток установившегося режима удобнее определять в комплексной форме, а затем от İ _уст. перейти к _уст. .

Свободная составляющая тока _св 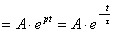, (2.15)

где 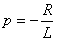, а .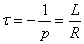

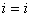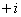Общий ток _пр.св 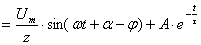. (2.16)

При 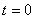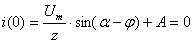(по первому закону коммутации). Откуда .

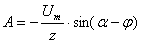Окончательно получим _св 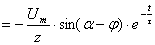, (2.17)

а 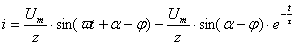. (2.18)

Из (2.18) видно, что ток состоит из двух частей – синусоидального тока с постоянной амплитудой и постоянного тока, убывающего по экспоненте. Величина общего тока существенно зависит от начального угла . Рассмотрим два крайних случая:

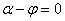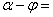а) или π.

В этом случае _св 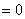и переходного процесса не будет, т.к. ток установившегося режима (а значит и связанная с ним энергия магнитного поля) в момент включения проходит через ноль. Скачка энергии не получается и ток сразу становится током установившегося режима;

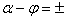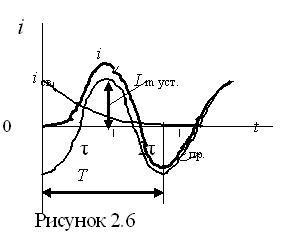
б) π /2.Здесь 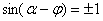принимает наибольшее значение и амплитуда тока переходного процесса также будет наибольшей. Это объясняется тем, что включение происходит в момент, когда ток установившегося режима максимален. Рассмотрим график рисунка 2.6.

Из графика видно, что ток особенно увеличивается во второй и третьей четверти первого периода, причем это увеличение сильно зависит от постоянной времени . Если велико, то ток через время Т/2 после включения может достичь почти удвоенной амплитуды I_{m уст.} (но ни при каких условиях не превзойдет 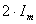_уст. ).

3 Лекция 3. Переходные процессы в цепях с двумя накопителями энергии

Цель лекции: познакомить с особенностями протекания переходных про-

цессов в цепях с последовательным соединением элементов 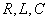и при их подключении на постоянное напряжение.

3.1 Переходный процесс в цепи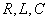

Так как расчет с конденсатором удобнее вести через , то все входя-щие в (3.1) величины выразим через это напряжение 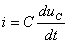; ; 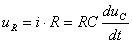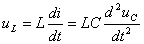. Подставив эти выражения в (3.1),

получим линейное дифференциальное уравнение второго порядка

.

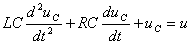Освободимся от коэффициента при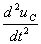

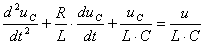, (3.2)

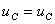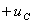где _{пр. св.}

Определяем _пр. по закону Ома. Принужденная составляющая зависит от формы приложенного напряжения. Если 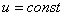, то _пр.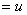. Если 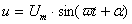, то напряжение и ток установившегося режима так же будут синусоидальными. В этом случае расчет ведется в комплексной форме, а затем находятся мгновенные значения как функции времени.

Находим u_{С св.}, которая и определяет длительность и характер переходного процесса.

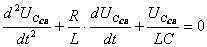_. (3.3)

Решением (3.3) будет: 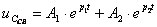. (3.4)

Корни характеристического уравнения 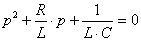определяются как 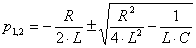. (3.5)

Значения корней зависят от соотношения параметров цепи. Может быть

три случая:

а) > .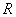

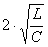
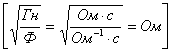При этом условии 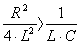и корни p₁, p₂ получаются вещественными, отрицательными, различными по величине.

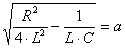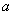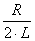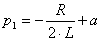В самом деле, если обозначить , где – вещественное число, меньше чем , то < 0; 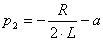< 0. (3.5а)

По абсолютной величине | 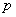₁ | < | 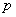₂ |. Такой режим называется апериодическим, т.к. ток и напряжение приближаются к установившемуся режиму, не меняя своего направления; б) 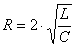. При этом условии 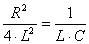и корни 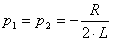также вещественные, отрицательные.

В этом случае 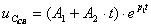. (3.6)

Этот режим называют критическим;

в) 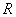< 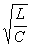. В этом случае корн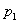и и 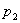комплексно-сопряженные с отрицательной вещественной частью ;

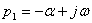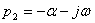, (3.7)

где 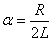– коэффициент затухания;

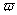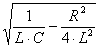
= - угловая частота собственных колебаний.

Такой режим называется периодическим или колебательным. Здесь происходит многократный обмен энергии между катушкой и конденсатором: энергия как бы переливается то в магнитное поле (когда растет ток), то в электрическое поле (когда растет напряжение на конденсаторе).

Постоянные интегрирования находятся из начальных условий.

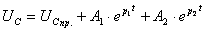. (3.8)

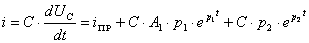. (3.9)

При : ,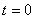

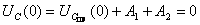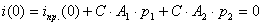. (3.10)

Из уравнений (3.10) легко определяются 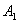и .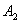

3.2 Включение цепи 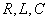на постоянное напряжение

Считаем, что цепь рисунка 3.1 включается на постоянное напряжение

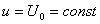u = U₀. Тогда 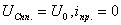и начальные условия (3.10) примут вид

;

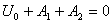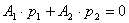, откуда , .

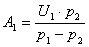С учетом полученного из (3.8) и (3.9.) имеем

,

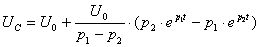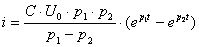. (3.11)

Исследуем полученные выражения при разных значениях корней.

а) апериодический режим В этом случае, согласно (3.5а), имеем

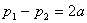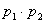> , > и > .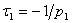

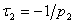В соответствии с этим график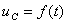и и 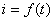имеют вид, представленный на рисунке 3.2.

б) колебательный режим. Так как в этом случае 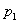и 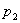– сопряженные комплексы, то 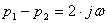, а ,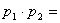

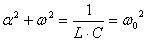где 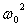- резонансная частота.

Подставим комплексные корни в выражения (3.11) и проведем некоторые

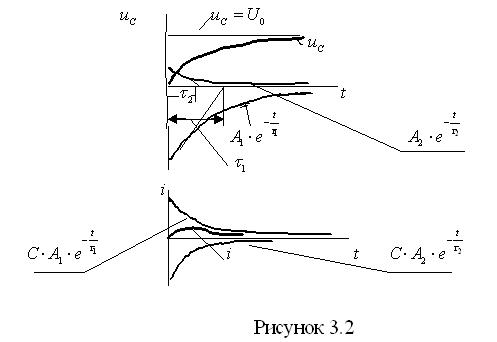
преобразования:

= ,

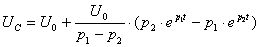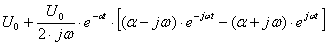т.к. 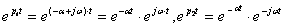. (3.12)

Переведем стоящие в скобках комплексы в показательную форму (рисунок 3.3)

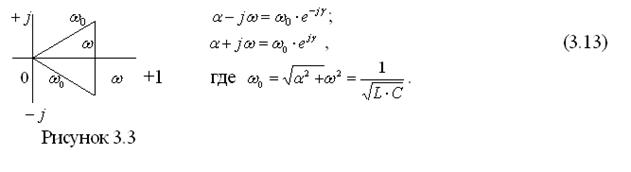
Подставив (3.13) в (3.12), получим

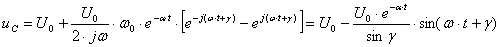. (3.14)

Подобным же образом можно преобразовать выражение тока

=.

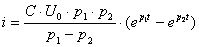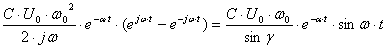(3.15)

Если учесть, что 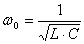, то можно получить ток в несколько ином виде: .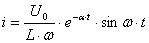

Для построения графиков 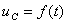и 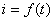нужно знать период собствен-

ных колебаний 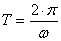и постоянную времени .

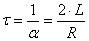Порядок построения затухающей синусоиды.

1. По обе стороны от оси строятся огибающие.

2. В том же масштабе, что и откладываются доли периода (при этом надо учитывать начальный угол).

3. Вписывается синусоида, которая в точках максимума касается огибающих.

Так как представляет собой разность постоянной величины и затухающей синусоиды, то для уменьшения графической работы на рисунке 3.4 эта синусоида построена с учетом знака, причем линия 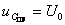использована как ось, т.е. сразу построен график 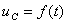, а не составляющие этого напряжения.

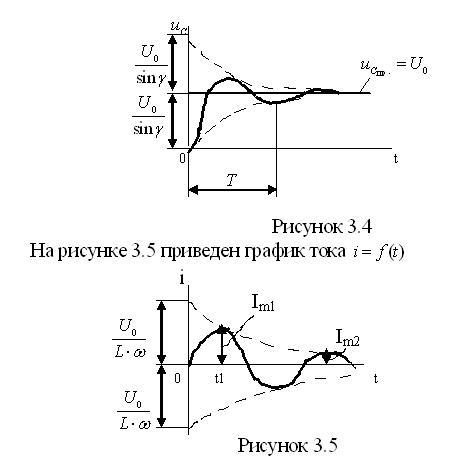
Если обозначить амплитуды напряжения и тока через 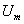и 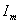, то их отношение 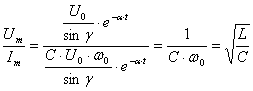, т.е. равно волновому сопротив-лению. Идеальный случай, когда 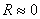и цепь можно считать сверхпроводя-щей. При этом 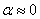и 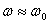. Но при 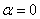энергия будет переходить от магнитного поля к электрическому без затухания. Отсюда еще одно название

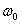- угловая частота незатухающих колебаний и 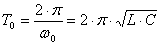- период собственных незатухающих колебаний. Угол 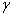при 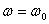получается равным 90⁰.

В реальных цепях 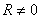и процесс будет затухающим. Для оценки быстро-

ты затухания сравним две соседние амплитуды тока (или напряжения) с одинаковым знаком. Пусть 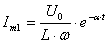, , 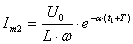т.к. 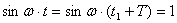. Отношение этих амплитуд 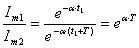(3.16)

называется декрементом колебания. Он не зависит от времени 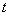, а зависит лишь от параметров цепи 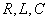. Обычно пользуются не им, а логарифмическим декрементом колебания

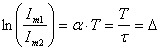. (3.17)

В колебательных контурах стремятся сделать как можно меньше, т.к. тогда затухание в контуре почти не сказывается. На графиках 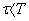, т.е. 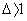и процесс затухает довольно быстро.

Дата добавления: 2014-01-04