Лекция 7. Основы спектрального анализа электрических цепей

Цель лекции: познакомить с частотными характеристиками, расчетом переходных процессов простых цепей с применением интеграла Фурье.

7.1 Частотные характеристики электрических цепей

При воздействии на вход электрической цепи какого-либо электрического сигнала во всех ее элементах возникнут реакции в виде токов и напряжений. Для линейных электрических цепей отношение спектра реакции к спектру воздействия является функцией параметров цепи и частоты. Если в качестве реакции выбрать спектр тока на входе пассивного линейного двухполюсника (рисунок 7.1), то отношение этого спектра тока к спектру приложенного напряжения будет представлять собою частотную характеристику двухполюсника

, (7.1)

где - частотный спектр приложенного напряжения, определяемый по известной функции приложенного напряжения 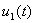из прямого преобразования Фурье

.

Частотная характеристика электрической цепи выражается комплексной функцией частоты и на комплексной плоскости может быть изображена вектором, модуль и фаза которого изменяются с увеличением частоты, описывая некоторую кривую (рисунок 7.2), называемой амплитудно-фазовой характеристикой.

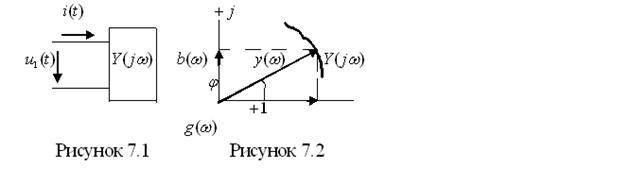
При анализе свойств двухполюсников можно вводить в рассмотрение наряду с амплитудной частотной характеристикой 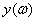и фазовой частотной характеристикой 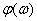еще их составляющие по осям комплексной плоскости.

Проекция вектора 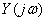на ось вещественных чисел дает вещественную частотную характеристику 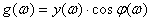. (7.2)

Подобным образом находится и мнимая частотная характеристика электрической цепи 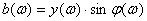. (7.3)

Физический смысл и 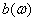становится ясным, если задаться любой фиксированной частотой . При этом частотный спектр входного напряжения и тока превратится в комплексные амплитуды входных напряжения и тока частоты 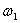, а частотная характеристика будет представлена комплексной проводимостью цепи

,

где 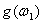- активная входная проводимость цепи;

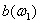- реактивная входная проводимость электрической цепи для частоты .

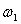Таким образом, вещественная частотная характеристика цепи представляет собой вещественную часть комплекса полной входной проводимости, заданную во всем диапазоне частот, а мнимая частотная характеристика – мнимую часть.

Экспериментально частотную характеристику следует снимать с помощью генератора синусоидальных напряжений переменной частоты при изменении последней от нуля до такого предела, при котором прекращается изменение характеристики или она становится ничтожно малой по сравнению с ее начальным значением.

На рисунке 7.3 приведены простые двухполюсники и соответствующий им ряд частотных характеристик .

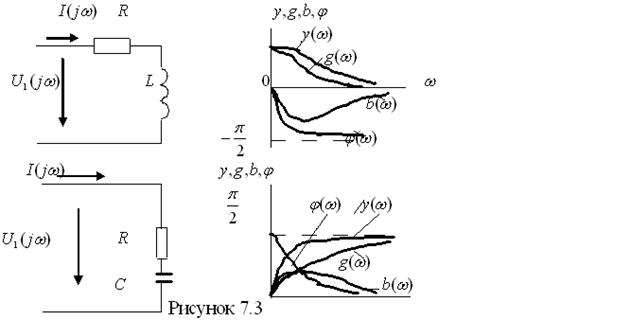
Комплексная проводимость цепи

.

Соответственно , .

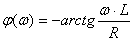Комплексная проводимость цепи :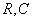

.

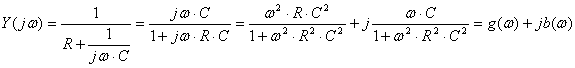Здесь , .

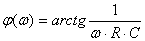В сложной пассивной линейной цепи можно в качестве реакции на входное напряжение выбрать не только входной ток, но и ток или напряжение в любой ветви схемы.

Если любую ветвь схемы полагать нагрузкой, то всю остальную часть схемы можно представить четырехполюсником с входным напряжением 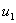и выходным 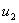(рисунок 7.4).

Как и частотная характеристика, комплексная передаточная функция может быть представлена или в виде амплитудно-частотной и фазо-частотной характеристик (7.5)

или в виде вещественной частотной и мнимой частотной характеристик

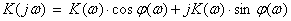. (7.6)

7.2 Расчет переходных процессов в цепях с применением интеграла Фурье

Частотным методом можно рассчитывать переходные процессы при включении (при 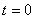) пассивных цепей, не обладающих запасом электромагнитной энергии, к источнику напряжения 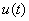. Цепи с начальным запасом энергии, т.е. с ненулевыми начальными условиями, этим методом не рассчитываются. Кроме того, функция u(t) должна быть абсолютно интегрируема, т.е. .

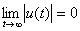Расчет электрических цепей осуществляется в следующем порядке:

- с помощью прямого преобразования Фурье определяется спектральная

характеристика приложенного напряжения ;

- находится комплексная передаточная функция или частотная характеристика 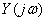рассчитываемой схемы в зависимости от определяемой величины;

- подсчитывается спектральная характеристика искомой величины, причем

все операции производятся также, как при расчете установившихся режимов цепей символическим методом

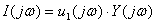или 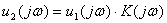. (7.7)

Обратный переход к временным функциям производится или непосредственно по обратному преобразованию Фурье

; , (7.8)

или же по теореме разложения, аналогичной той, которую применяют в операторном методе при использовании преобразования Лапласа

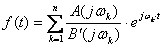. (7.9)

В теореме разложения, полученной ранее, следует заменить 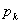на .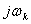

Пример - Рассчитать напряжение на конденсаторе 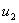при включении на постоянное напряжение электрической цепи рисунка 7.5. Параметры цепи 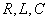заданы.

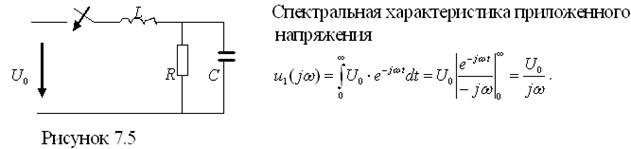
Находим комплексную передаточную функцию в символической форме .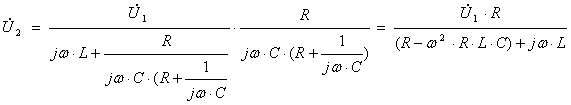

Следовательно, .

Спектр выходного напряжения

.

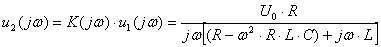Оригинал выходного напряжения определяется или из выражения

,

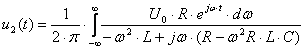или по теореме разложения

.

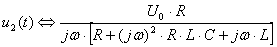Применив к последнему выражению теорему разложения, после преобразований получится следующий оригинал выходного напряжения

,

где .

Как видно из приведенного примера, отыскание оригинала по обратному преобразованию Фурье сводится к вычислению интеграла, причем подынтегральная функция может быть весьма сложной. Она еще более усложняется, если напряжение на входе цепи изменяется по какому-либо сложному закону.

Применение теоремы разложения в обычной ее форме при замене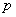на 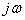значительно упрощает отыскание оригинала, но в этом случае частотный метод вырождается в обычный операторный метод расчета и особого интереса не представляет. Аналитическое решение задач операторным методом становится весьма затруднительным, если включаемая цепь имеет более двух мест накопления энергии. В этом случае в операторных уравнениях знаменатель будет представлять собой полином степени выше второй и решение такого уравнения для отыскания корней знаменателя становится очень трудным. В таких случаях задача может быть решена с помощью частотного метода.

Дата добавления: 2014-01-04