Доверительный интервал. Доверительная вероятность

Другими словами в результате эксперимента требуется не только найти для параметра a подходящее численное значение, но и оценить его точность и надежность. Требуется знать – к каким ошибкам может привести замена неизвестного параметра его точечной оценкой 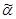(точечная оценка – оценка, которая определяется одним числом) и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за известные пределы. Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка 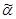в значительной мере случайна и приближенная замена a на 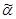может привести к серьезным ошибкам. Вследствие этого пользуются интервальными оценками. Оценка, определяемая двумя числами – концами интервала, называется интервальной.

Чтобы дать представление о точности и надежности оценки 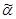, в математической статистике пользуются так называемыми доверительными интервалами и доверительными вероятностями. Понятие доверительная вероятность равнозначно понятию надежности.

Все оценки параметров распределения выборки носят случайный характер и от параметров генеральной совокупности могут сильно отличаться. Чтобы им доверять нужно, чтобы интервал (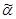-d; 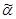+d) с заданной надежностью g накрывал бы неслучайное значение параметра генеральной совокупности a.. Такой интервал называется доверительным. Обычно величину доверительной вероятности принимают в пределах от 0,95 до 0,99.

Нахождение доверительных интервалов основано на том, что математическое ожидание, дисперсия и сама оценка распределена по нормальному закону. Вероятность того, что оценка не превысит интервал d – подчиняется нормальному закону:

.

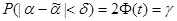Неравенство в круглых скобках

где 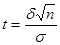– находится с помощью таблиц Лапласа, п – объём выборки, s – среднее квадратичное отклонение.

Следовательно, Ф(t)=g/2. По таблице функции Лапласа находят аргумент , которому соответствует значение функции Лапласа, равное g/2.

Например: в результате равноточных измерений получили ошибку s=30², требуется определить количество опытов п для обеспечения заданной точности измерений d =5² (доверительный интервал) и доверительной вероятности (надёжности) g=0,9.

По таблице Лапласа находим t =1,643, 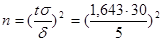=97 опытов.

Дата добавления: 2014-01-04