
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Однофакторная линейная регрессия
|
|
|
|
При обработке результатов пассивных экспериментов реально установить лишь однофакторные регрессионные зависимости.
Однофакторная линейная регрессия – регрессионная зависимость между двумя переменными у и х (модель) вида
у=b0+b1x+e,
где у – отклик, х – фактор, е – аддитивная помеха, величина, учитывающая случайные ошибки измерений, случайные шумы, влияние неучтенных факторов. При определении уравнения регрессии целесообразно принять условие, что математическое ожидание аддитивной помехи равно нулю: М(е)=0. В этом случае уравнение регрессии будет иметь вид у=b0+b1x.
1) При построении теоретической регрессионной зависимости оптимальной является такая функция, в которой неизвестные параметры b0 и b1 выбираются таким образом, чтобы сумма квадратов отклонений фактических значений отклика у от прогнозных (полученных по уравнению регрессии)  была минимальна (это – метод наименьших квадратов (МНК)):
была минимальна (это – метод наименьших квадратов (МНК)):
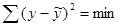
Чтобы найти минимум функции, надо вычислить частные производные по каждому из параметров b0 и b1 и приравнять их к нулю. Обозначим 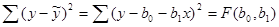 . Тогда
. Тогда


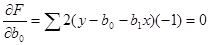 Þ
Þ 
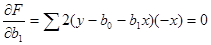 Þ
Þ 
 |

 Þ
Þ 
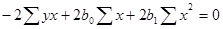 Þ
Þ 
Примечание: Sb0=nb0. Делим обе части уравнений системы на n (объем выборки). Получим:
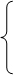
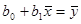 Þ
Þ 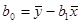
 Þ
Þ 
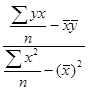 .
.
Коэффициент b1 называется коэффициентом регрессии и показывает среднее изменение отклика при изменении фактора на одну единицу.
2) Тесноту связи отклика и фактора оценивает линейный коэффициент корреляции Пирсона r, который можно вычислить, например, по следующей формуле:
Критерием близости корреляционной связи между х и у к линейной зависимости является коэффициент корреляции Пирсона r, который можно вычислить, например, по следующей формуле:
 ,
,
где sх, sу – средние квадратические отклонения случайных величин X и Y.
Линейная вероятностная зависимость случайных величин заключается в том, что при возрастании одной случайной величины другая имеет тенденцию возрастать (или убывать) по линейному закону. Если случайные величины X и Y связаны строгой линейной функциональной зависимостью, например, y=b0+b1x1, то коэффициент корреляции будет равен r=±1; причем знак соответствует знаку коэффициента b1. Это значит, что каждому значению х будет соответствовать только одно значение у. При r=0 линейная корреляционная связь между х и у отсутствует, они либо независимы, либо существует нелинейная регрессия. Если величины X и Y связаны произвольной стохастической зависимостью, то коэффициент корреляции будет изменяться в пределах −1<r <+1.
Качественная оценка тесноты связи может быть выявлена на основе шкалы Чеддока.
| Теснота связи | Значение |r| |
| Слабая | 0,1 – 0,3 |
| Умеренная | 0,3 – 0,5 |
| Заметная | 0,5 – 0,7 |
| Высокая | 0,7 – 0,9 |
| Весьма высокая | 0,9 – 0,99 |
Коэффициент детерминации – для парной линейной регрессии – это квадрат линейного коэффициента корреляции. Величина r2 показывает, сколько процентов отклика объясняется с помощью включенного в модель фактора. Чем больше, тем лучше построенная модель. Если, r2 < 30%, то прогнозировать по такой модели нецелесообразно. В технических системах, если r2 <0,75, то уравнение регрессии считается неработоспособным.
Пример: Пусть имеется следующий статистический ряд парных измерений.
Нужно найти уравнение линейной регрессии, оценить тесноту связей и оценить степень достоверности.
Расчёт удобно вести в табличной форме.
 ;
;  ;
;
 ;
; 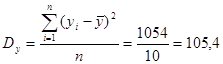 ;
;
b1=  ;
;  ;
;
Уравнение регрессии:  .
.
Таблица расчёта
| х | у | х2 | у2 | ху | (х- )2 )2
| (у-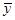 )2 )2
| 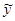
| 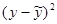
| |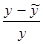 | |
| 
| |
| 20,25 | 7,03 | 0,9409 | 0,12125 | 255,0409 | |||||||
| 12,25 | 10,58 | 0,1764 | 0,038182 | 154,2564 | |||||||
| 6,25 | 14,13 | 0,0169 | 0,00929 | 78,6769 | |||||||
| 2,25 | 17,68 | 2,8224 | 0,105 | 28,3024 | |||||||
| 0,25 | 21,23 | 0,0529 | 0,01095 | 3,1329 | |||||||
| 0,25 | 24,78 | 1,4884 | 0,046923 | 3,1684 | |||||||
| 2,25 | 28,33 | 1,7689 | 0,04926 | 28,4089 | |||||||
| 6,25 | 31,88 | 0,0144 | 0,00375 | 78,8544 | |||||||
| 12,25 | 35,43 | 2,0449 | 0,04206 | 154,5049 | |||||||
| 20,25 | 38,98 | 4,0804 | 0,049268 | 255,3604 | |||||||
| S | 82,5 | 13,4065 | 0,475933 | 1039,707 | |||||||
| Ср. | 5,5 | 8,25 | 105,4 | 0,04759 |
Теснота связи по критерию корреляции Пирсона 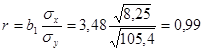 – хорошая (весьма высокая по шкале Чеддока), где
– хорошая (весьма высокая по шкале Чеддока), где  ,
, 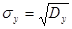 .
.
Коэффициент детерминации r2=0,992=0,98 показывает, что 98% функции отклика характеризуется изменением фактора х и только 2% другими причинами. Следовательно, найденное уравнение работоспособно.
3) Для практического использования полученная математическая модель процесса должна быть проверена на достоверность и адекватность. Суть такой проверки состоит в сопоставлении полученной теоретической функции у=f(х) с результатами измерений.
3.1) Чтобы иметь общее представление о качестве модели, из относительных отклонений по каждому наблюдению определяют среднюю ошибку аппроксимации:
 .
.
Величина ошибки аппроксимации не должна превышать 10-12%.
Рассчитаем ошибку аппроксимации для приведённого примера.
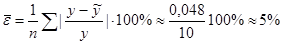 .
.
Очевидно, что полученная модель достаточно точно аппроксимирует результаты измерений.
3.2) В практике оценки адекватности применяют различные статистические критерии. Оценка качества уравнения регрессии проводится на основе критерия Фишера (F -критерий).
Применение этого критерия основано на следующей идее. Общая сумма квадратов отклонений переменной у от среднего значения 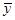 можно разложить на две составляющие:
можно разложить на две составляющие: 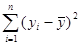 =
= +
+
Одна часть – «объяснённая», описывается регрессионным уравнением
– «объяснённая», описывается регрессионным уравнением  =b0+b1x.
=b0+b1x.
Вторая  – «необъяснённая», не описывается уравнением регрессии и характеризует отклонение выходной величины относительно полученной математической модели.
– «необъяснённая», не описывается уравнением регрессии и характеризует отклонение выходной величины относительно полученной математической модели.
Эти суммы квадратов приводятся к сравнимому виду, путём деления на соответствующее число степеней свободы. При этом получают несмещённые оценки общей дисперсии эксперимента, факторной и остаточной.
Общая дисперсия эксперимента (с учётом объяснённой и необъяснённой ошибки) равна  , исправленная общая дисперсия, являющаяся статистической оценкой генеральной дисперсии выборки
, исправленная общая дисперсия, являющаяся статистической оценкой генеральной дисперсии выборки 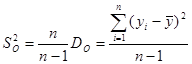 .
.
Исправленная факторная дисперсия, характеризующая рассеяние выходного параметра модели относительно среднего значения –  . Здесь k – число степеней свободы, на единицу меньшее количества искомых коэффициентов уравнения регрессии (количество факторов равно k, количество искомых коэффициентов уравнения регрессии – k+1, число степеней свободы исправленной факторной дисперсии – (k+1)-1=k).
. Здесь k – число степеней свободы, на единицу меньшее количества искомых коэффициентов уравнения регрессии (количество факторов равно k, количество искомых коэффициентов уравнения регрессии – k+1, число степеней свободы исправленной факторной дисперсии – (k+1)-1=k).
Исправленная остаточная дисперсия, обусловленная влиянием неучтенных факторов и ошибками измерений в ходе проведения эксперимента, характеризующая отклонение результатов опыта от линии регрессии – 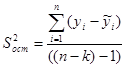 .
.
Сопоставляя факторную и остаточную дисперсии, соотнесённые на одну степень свободы, получают экспериментальное значение критерия Фишера, которое сравнивают с теоретическим (табличным) коэффициентом Fтабл(α, f1, f2) при уровне значимости a и степенях свободы исправленных дисперсий числителя – f1=k и знаменателя – f2=(п- k)-1.
Условие адекватности уравнения регрессии при F -критерии, рассчитанным данным способом заключается в выполнении неравенства:
F=DФ/Dост> Fтабл(α, f1, f2).
Уровень значимости a обычно берётся равным a=0,05. Он связан с доверительной вероятностью g=1-a. Следовательно, g=1-0,05=0,95.
Если фактическое значение F -критерия, определённого как отношение факторной дисперсии к остаточной, больше табличного Fтабл(α, f1, f2), то признаётся статистическая значимость уравнения регрессии.
В нашем примере
DФ=1039,707/ 1=1039,707;
Dост= 13,4/ 8=1,675;
F=1039,707/ 1,675»621> Fтабл(0,05, 1, 8)»239.
Fтабл(α, f1, f2) можно определить с помощью функции Fраспробр в EXEL.
Значит в 95% случаев уравнение регрессии статистически значимо и отражает существенную связь между фактором и функцией отклика.
Если по критерию Фишера модель неадекватна, то при неизменном составе входных факторов, следует выдвинуть конкурирующую гипотезу о нелинейном виде математический модели и весь процесс вычислений повторить для получения модели в виде неполного квадратного или полного квадратного полинома. Так, повышая постепенно степень полинома, можно получить в конечном итоге адекватную математическую модель. Критерий Фишера обычно принимается для оценки адекватности малых выборок. В больших выборках применяют, например, критерий Пирсона.
3.3) При проверке достоверности модели проверяется также значимость коэффициентов регрессии. Для этого используется t-критерий Стьюдента.
Экспериментальное значение критерия Стьюдента для оценки значимости коэффициентов регрессии рассчитывается на основе вычисления стандартных (среднеквадратических) отклонений.
Стандартное (среднее квадратическое) отклонение свободного члена уравнения линейной регрессии b0 можно рассчитать по формуле
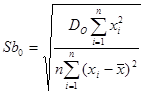 .
.
Стандартное отклонение коэффициента линейной регрессии b1
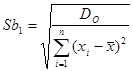

Экспериментальные значения t -критериев Стьюдента для коэффициентов уравнения регрессии
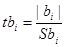 .
.
Опытные значения критериев сравниваются с табличным tт (a, t1) для заданного уровня значимости и числа степеней свободы t1=п-(k+1-1)-1=n-k-1.
Если t> tт (a, t1), то коэффициенты регрессии являются значимыми. tт (a, t1) можно определить с помощью функции Стьюдраспробр в EXEL.
В нашем примере:
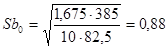 ;
; ³ tт (0,05, 8)=1,86;
³ tт (0,05, 8)=1,86;
 ;
;  ³ tт (0,05, 8)=1,86.
³ tт (0,05, 8)=1,86.
Следовательно, коэффициенты регрессии с вероятностью 95% являются надёжными.
3.4) На основе t -критерия Стьюдента могут быть определены доверительные интервалы, куда с заданной доверительной вероятностью будет входить истинные значение коэффициентов регрессии.
Для этого рассчитываются предельные ошибки по формуле
 ,
,
где Sbi – среднее квадратическое отклонение коэффициента.
Для парной линейной регрессии:  и
и  .
.
Таким образом, доверительные интервалы для коэффициентов регрессии равны:
b0-D b0<b0< b0+D b0 и b1-D b1<b1< b1+D b1.
В нашем примере предельные ошибки равны:
 =2,31×0,88=2,03 и
=2,31×0,88=2,03 и  =2,31×0,18=0,42.
=2,31×0,18=0,42.
Доверительные интервалы: 1,45< b0<95,51 и 3,13< b1<3,97.
Следовательно, на основе нашего уравнения можно делать прогноз. В 9 5% случаев при увеличении фактора х на одну относительную единицу, выходной параметр увеличиться в среднем в 3,55 раза и может составить от 3,13 до 3,97 условных единиц.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 9907; Нарушение авторских прав?; Мы поможем в написании вашей работы!