Симплекс-планы

Дробный факторный эксперимент

При увеличении числа факторов количество опытов резко увеличивается.

Количество факторов	Количество параметров линейной модели	Число опытов ПФЭ	Разность между числом опытов и количеством параметров
…	…	…	…

Разность между числом опытов и количеством параметров линейной модели с увеличением числа факторов становится чрезмерно большой.

Для сокращения числа опытов используется дробный факторный эксперимент (ДФЭ) или так называемые дробные реплики.

Суть ДФЭ заключается в том, что в матрице планирования дополнительным факторам присваивают вектор-столбцы, принадлежащие взаимодействиям факторов, а этим взаимодействием пренебрегают. При этом информация о взаимодействиях теряется, но существенно сокращается количество опытов.

Например, при ПФЭ типа 2² можно вычислить четыре коэффициента и представить результаты в виде полинома второго порядка у=b₀+b₁·x₁+b₂·x₂+ b₁₂·x₁·x₂.

Однако, если есть основания считать, что в выбранных интервалах процесс может быть описан линейной моделью, то достаточно определить коэффициенты b₀, b₁, b₂. Оставшуюся неиспользованной информацию можно применить для минимизации числа опытов и для оценки влияния ещё одного фактора.

В рассматриваемом случае неиспользованный вектор-столбец можно присвоить новому фактору. Его коэффициент будет рассчитываться путём умножения результатов опытов на «1» со знаком вектор-столбца, вместо которого этот столбец вводится.

Например, при исследовании трёхфакторной модели 2³ можно получить линейное приближение некоторого участка поверхности отклика: у=b₀+b₁·x₁+b₂·x₂+ b₃·x₃. Решение данной задачи можно получить, ограничившись четырьмя опытами, т.е. половиной ПФЭ. Это – так называемая полуреплика. Обозначается – 2^3-1.

Бывает, что используют и большие дробности, например 1/4 (N=n^k-2), 1/8 (N=n^k-3) или 1/16 (N=n^k-4) реплики. Число опытов в дробной реплике (N=n^k-p) должно удовлетворять равенству:

k+1≤N≤2^k,

где k – число факторов.

Когда число опытов равно числу коэффициентов регрессии N=k+1, то дробная реплика представляет собой насыщенный план.

Линейные (двухуровневые) планы типа 2^k и 2^k-p (где р - число линейных эффектов, приравненных к эффектам взаимодействия) обладают следующими положительными свойствами:

1. Планы ортогональны;

2. Каждый коэффициент определяется по результатам всех N опытов;

3. Планы обладают свойствами ротабельности;

4. Планы обладают свойствами D -оптимальности.

Симплекс (simplex – с латинского простой) – это простейшее тело в k -мерном пространстве, имеющее (k+1) вершину. В одномерном пространстве – это отрезок, в двухмерном – треугольник, в четырёхмерном – 4-х гранная пирамида, в k - мерном пространстве – это многогранник с (k +1) вершиной.

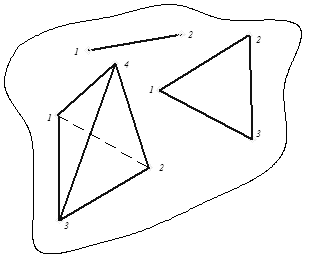
Рис.13 Симплексы различных размерностей

В симплекс-планах опыты выполняют в точках, соответствующих вершинам симплекса. Планы такого типа – насыщенные. Количество опытов равно числу коэффициентов регрессии. Например, для регрессии вида 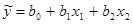выполняется три опыта при двух факторах.

Свойства симплекс-планов зависит от свойств симплексов.

Симплекс называется правильным, если для него расстояние между двумя любыми вершинами есть величина постоянная.

Симплекс называется центрированным, если для него справедливо соотношение .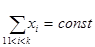

Если симплекс-план построен на базе правильного или центрированного симплекса, то он будет называться правильным или центрированным.

Симлекс-план представляет собой минимальный случай ДФЭ. Он содержит (k +1) точек (опытов). Например, число факторов k=4, тогда количество опытов N=4+1=5.

Поскольку существуют различные способы задания п- мерных симплексов, то для одной и той же размерности факторного пространства возможны различные симплекс-планы.

Для k>2 рекомендуется использовать готовые матрицы симплексы.

Например, центрированный правильный симплекс-план задаётся матрицей

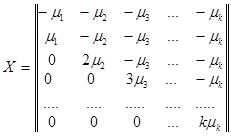, где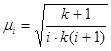, i£ k.

Соответственно при k=2 матрица симплекс-плана будет иметь следующий вид.

i k	x1 (i=1)	x2 (i=2)
1	-0,866	-0,5
2	0,866	-0,5
3	0	+1

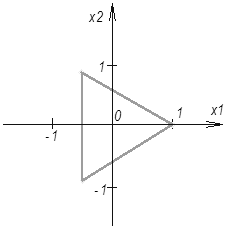
Рис.14 Центрированный правильный симплекс (k=2)

Симплекс-планы можно составить с целочисленной решёткой. В этом случае элементы матрицы будут принимать только два значения: +1 и -1, подобно ПФЭ и ДФЭ.

Однако планы с целочисленной решёткой могут быть построены только для определённых значений факторов k.

Если факторное пространство таково, что N=k+1 делится на 4 без остатка, то возможны правильные целочисленные симплексы.

№ опыта	Х1	Х2	Х3
	-1	+1	+1
	+1	-1	+1
	+1	+1	-1
	+1	+1	+1

Более того, если N=k+1 можно представить в виде N=k+1=2^s=2^k-p для k=3, 7, 15, где s – целое число, то симплекс-план является в тоже время планом ДФЭ типа 2^k-p . Например, k=7; N=7+1=8=2³=2^7-4.

Для k=11, 19, 23 разработан специальный вектор-столбец, с помощью которого формируется вся матрица плана.

Векторы-столбцы планов с k=11, 19, 23

n	N	Комбинации знаков
		+ + - + + + - - - + - + + - - + + + + - + - + - - - - + + - - + + + + + - + - + + - - + + - - + - + - - - - -

При составлении плана сначала записывается вспомогательная матрица размера k×k. В качестве первого столбца выписывается последовательность единиц со знаками из приведённой таблицы. Второй столбец – результат циклического сдвига первого столбца вниз на одну позицию, где в качестве первого элемента ставится последний элемент. Третий столбец – циклический сдвиг второго и т.д. Собственная матрица плана получается путём дополнения вспомогательной матрицы дополнительной (+1) строкой, состоящей из k элементов, равных -1.

.

Получаемые различными способами симплекс-планы в определённом смысле эквивалентны, так как симплексы одинаковой размерности всегда могут быть преобразованы один в другой с помощью невырожденного линейного преобразования. Фактически они отличаются лишь размерами, ориентацией и расположением в пространстве. Натуральные значения факторов х_i при фиксированном центре плана зависят от шагов варьирования ∆х_i.

Если сиплекс правильный и центрированный, то коэффициенты регрессии будут вычисляться по тем же формулам, что и в ПФЭ и в ДФЭ.

Симплекс-планы рекомендуется использовать на стадии предварительного исследования объекта и при поиске экстремальных значений целевой функции.

Дата добавления: 2014-01-04