Основы теории подобия

При разработке новых технологических процессов и аппаратов для их осуществления очень часто необходимо использовать экспериментальные данные, характеризующие конкретное производство. Исследователю при этом необходимо решить ряд задач.

1) Каким образом от лабораторных результатов и размеров моделирующего стенда перейти к промышленному процессу и установке?

2) Какое минимальное число величин, характеризующих процесс, необходимо измерять в ходе лабораторного эксперимента, не теряя при этом его физической достоверности?

3) Какое минимальное число экспериментов необходимо провести для получения реальной физической картины осуществляемого процесса?

На все эти вопросы помогает ответить теория подобия, которая устанавливает связь между группами подобных явлений.

Выводы теории подобия строятся на основании анализа дифференциальных уравнений, описывающих исследуемый процесс.

Однако одни и те же дифференциальные уравнения, как правило, описывают целый класс различных по своему характеру процессов. Для того чтобы рассмотреть математическую модель изучаемого явления, необходимо дополнить ее параметрами, кон­кретизирующими условия осуществления процесса, отличающего его от других (сходных) процессов.

Эти параметры называются условиями однозначности и включают:

· геометрические условия, характеризующие размеры и форму аппарата, в котором осуществляется процесс;

· физические свойства сред, взаимодействующих в процессе;

· граничные условия, характеризующие взаимодействие сред с телами, ограничивающими объем протекающего процесса;

· параметры, характеризующие начальное состояние рассматриваемой системы. В соответствии с теоремой Кирпичева – Гухмана подобны явления, описываемые одной и той же системой дифференциальных уравнений, у которых соблюдается подобие условий однозначности.

Отсюда следует, что подобные явления повторяют себя в различных масштабах, включающих геометрическое подобие систем, временное подобие, подобие физических величин, характеризующих процесс, подобие граничных и начальных условий.

Таким образом, в подобных процессах должны выполняться следующие условия:

· геометрическое подобие:

где l₁, l₂, l₃ - характерные размеры первого аппарата; L₁, ₂, L₃ – характерные размеры второго аппарата, сходственные с размерами первого аппарата; К₁ – коэффициент подобия линейных размеров (соответствующие углы подобных конструкций должны быть равны);

· временное подобие:

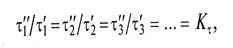
где τ₁^’, τ₁^’, τ₁^’ – интервалы времени, характеризующие стадии первого процесса; τ₁^’’, τ₁^’’, τ₁^’’ – интервалы времени, характеризующие сходные стадии подобного процесса; К_τ - коэффициент временного подобия (гомохронности). При К_τ = 1 процессы называются синхронными;

· подобие физических величин:

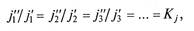
где j₁^’, j₂^’, j₃^’ – характерные физические величины в первом процессе (плотность, вязкость, теплоемкость и т.д.); j₁^”, j₂^’’, j₃^’’ – сходные физические величины во втором процессе; К _j - коэффициент подобия физических величин;

· подобие начальных и граничных условий предполагает постоянство отношения основных параметров в начале и на границе реального процесса и модели, т. е. соблюдение геометрического, временного и физического подобия.

Отношение двух одноименных физических величин называется параметрическими критериями, или симплексами.

Выбор критериев для подобных процессов не является произ­вольным. Покажем это на примере второго закона механики

где f – сила; т – масса; w – скорость; τ – время.

в случае рассмотрения двух подобных процессов оба они описываются уравнением (В.6), нос разными характерными параметрами

Выраженные в безразмерном виде уравнения (В.7) запишутся

Входящие в них основные переменные в этом случае могут быть выражены в соответствии с подобием условий однозначности как

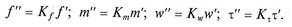
После подстановки их в соответствующее безразмерное выражение получаем

Поскольку второй сомножитель равен единице (уравнение (В.8)), для подобных процессов должно выполняться условие:

Если заменить в уравнении (В.9) коэффициенты подобия отношением самих величин, то получим

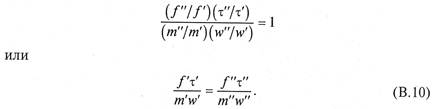
Данные безразмерные комплексы носят название критериев подобия и обычно обозначаются первыми двумя буквами фамилий ученых, получивших их. Так безразмерный комплекс (В.10) называется критерием Ньютона

При этом следует помнить, что для подобных процессов сами параметры, входящие в критерии, могут меняться во времени и пространстве, но в сходственных точках объема и времени они принимают одно и то же значение.

При применении теории подобия различают определяемые и определяющие критерии. Первые нельзя определить, используя величины, входящие в условия однозначности, вторые – можно определить с помощью этих величин.

Целью проведения и обработки экспериментальных исследований является установление функциональной зависимости между определяемыми и определяющими критериями.

Критерии подобия обычно получают следующим образом:

записывают дифференциальное уравнение, описывающее рассматриваемый процесс (В.6);

приводят его к безразмерному виду путем деления одной части уравнения на другую, либо всех слагаемых на одно из выбранных (В.8);

опускают символы дифференцирования. При этом степени дифференциалов при переменных сохраняются (В.11).

Таким образом, анализ процесса с позиций теории подобия позволяет:

определить влияющие на процесс параметры, которые следует измерять в ходе эксперимента;

планировать и проводить эксперимент, варьируя критерии подобия;

распространять результаты экспериментальных исследований на подобные процессы.

При этом следует помнить, что теорию подобия можно применять только к процессам, для которых известны описывающие их дифференциальные уравнения.

В противном случае необходимо использовать другие методы

обработки результатов эксперимента (методы анализа размерностей, регрессионный и т.д.).

РАЗДЕЛ I

Дата добавления: 2014-01-04