Виды погрешностей измерения

Погрешность измерения – это отклонение результата измерений от истинного значения измеряемой величины. Чем меньше погрешность, тем выше точность. Виды погрешностей представлены на рис. 11.

Систематическая погрешность – составляющая погрешности измерения, остающаяся постоянной или закономерно изменяющаяся при повторных измерениях одной и той же величины. К систематическим относятся, например, погрешности от несоответствия действительного значения меры, с помощью которой выполнялись измерения, ее номинальному значению (погрешности показания прибора при неправильной градуировке шкалы).

Систематические погрешности могут быть изучены опытным путем и исключены из результатов измерений путем введения соответствующих поправок.

Поправка – значение величины, одноименной с измеряемой, прибавляемое к полученному при измерениях значению с целью исключения систематической погрешности.

Случайная погрешность – это составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Например, погрешности вследствие вариации показаний измерительного прибора, погрешности округления или отсчитывания показаний прибора, колебаний температуры в процессе измерения и т.д. Их нельзя установить заранее, но их влияние можно уменьшить путем многократных повторных измерений одной величины и обработкой опытных данных на основе теории вероятности и математической статистики.

К грубым погрешностям (промахам) относятся случайные погрешности, значительно превосходящие погрешности, ожидаемые при данных условиях измерения. Например, неправильный отсчет по шкале прибора, неправильная установка измеряемой детали в процессе измерения и т.д. Грубые погрешности не принимаются во внимание и исключаются из результатов измерения, т.к. являются результатом просчета.

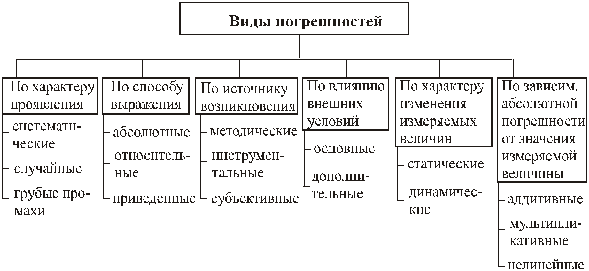
Рис.11. Классификация погрешностей

Абсолютная погрешность – погрешность измерения, выраженная в единицах измеряемой величины. Абсолютную погрешность определяют по формуле.

= изм_. – , (1.5)

где изм_. - измеренное значение; - истинное (действительное) значение измеряемой величины.

Относительная погрешность измерения – отношение абсолютной погрешности к истинному значению физической величины (ФВ):

= или 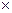100% (1.6)

На практике вместо истинного значения ФВ используют действительное значение ФВ, под которым подразумевают значение, отличающееся от истинного так мало, что для данной конкретной цели этим отличием можно пренебречь.

Приведенная погрешность – определяется как отношение абсолютной погрешности к нормирующему значению измеряемой физической величины, то есть:

, (1.7)

где X_N – нормирующее значение измеряемой величины.

Нормирующее значение X_N выбирают в зависимости от вида и характера шкалы прибора. Это значение принимают равным:

- конечному значению рабочей части шкалы. X_N = X_К, если нулевая отметка – на краю или вне рабочей части шкалы (равномерная шкала рис.12, а - X_N = 50; рис. 12, б - X_N = 55; степенная шкала - X_N = 4 на рис.12, е);

- сумме конечных значений шкалы (без учета знака), если нулевая отметка – внутри шкалы (рис.12, в - X_N = 20 + 20 = 40; рис.12, г - X_N = 20 + 40 = 60);

- длине шкалы, если она существенно неравномерна (рис.12, д). В этом случае, поскольку длина выражается в миллиметрах, то абсолютная погрешность выражается также в миллиметрах.

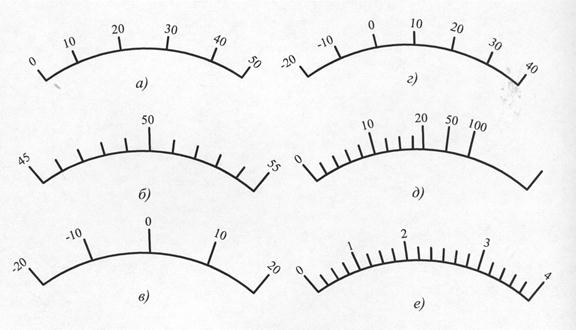
Рис. 12. Виды шкал

Погрешность измерения является результатом наложения элементарных ошибок, вызываемых различными причинами. Рассмотрим отдельные составляющие суммарной погрешности измерений.

Методическая погрешность обусловлена несовершенством метода измерения, например, неправильно выбранной схемой базирования (установки) изделия, неправильно выбранной последовательностью проведения измерений и т.п. Примерами методической погрешности являются:

- Погрешность отсчитывания – возникает из-за недостаточно точного отсчитывания показаний прибора и зависит от индивидуальных способностей наблюдателя.

- Погрешность интерполяции при отсчитывании – происходит от недостаточно точной оценки на глаз доли деления шкалы, соответствующей положению указателя.

- Погрешность от параллакса возникает вследствие визирования (наблюдения) стрелки, расположенной на некотором расстоянии от поверхности шкалы в направлении не перпендикулярном поверхности шкалы (рис. 13).

- Погрешность от измерительного усилия возникают из-за контактных деформаций поверхностей в месте соприкосновения поверхностей измерительного средства и изделия; тонкостенных деталей; упругих деформаций установочного оборудования, например, скоб, стоек или штативов.

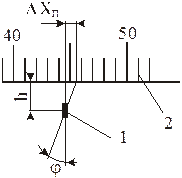Рис.13. Схема возникновения погрешности от параллакса.

Погрешность от параллакса _n прямопропорциональна расстоянию h указателя 1 от шкалы 2 и тангенсу угла φ линии зрения наблюдателя к поверхности шкалы _n= h × tg φ (рис. 13).

Инструментальная погрешность – определяется погрешностью применяемых средств измерения, т.е. качеством их изготовления. Примером инструментальной погрешности является погрешность от перекоса.

Погрешность от перекоса возникает в приборах, в конструкции которых не соблюден принцип Аббе, состоящий в том, что линия измерения должная являться продолжением линии шкалы, например перекос рамки штангенциркуля, изменяет расстояние между губками 1 и 2 (рис. 14).

Погрешность определения измеряемого размера из-за перекоса _пер.= l × cosφ. При выполнении принципа Аббе l × cosφ = 0 соответственно _{пер .} = 0.

Субъективные погрешности связаны с индивидуальными особенностями оператора. Как правило, эта погрешность возникает из-за ошибок в отсчете показаний и неопытности оператора.

Рассмотренные выше разновидности инструментальной, методической и субъективной погрешностей вызывают появление систематических и случайных погрешностей, из которых складывается суммарная погрешность измерения. Они также могут приводить к грубым погрешностям измерений. В суммарную погрешность измерения могут входить погрешности, обусловленные влиянием условий измерений. К ним относятся основные и дополнительные погрешности.

Рис.14. Погрешность измерения от перекоса губок штангенциркуля.

Основная погрешность – это погрешность средства измерения при нормальных условиях эксплуатации. Как правило, нормальными условиями эксплуатации являются: температура 293 ± 5 К или 20 ± 5°С, относительная влажность воздуха 65 ± 15% при 20°С, напряжение в сети питания 220 В ± 10% с частотой 50 Гц ± 1%, атмосферное давление от 97,4 до 104 КПа, отсутствие электрических и магнитных полей.

В рабочих условиях, зачастую отличающихся от нормальных более широким диапазоном влияющих величин, появляется дополнительная погрешность средств измерений.

Дополнительная погрешность возникает в результате нестабильности режима работы объекта, электромагнитных наводок, колебания параметров источников питания, наличия влаги, ударов и вибраций, температуры и т.п.

Например, отклонение температуры от нормального значения +20°С приводит к изменению длины деталей измерительных средств и изделий. Если невозможно выполнить требования к нормальным условиям, то в результат линейных измерений следует вводить температурную поправку D Х_t, определяемую по формуле:

D Х_t = Х_{ИЗМ ..} [α₁ (t₁-20)- α₂ (t₂-20)] (1.8)

где Х_{ИЗМ .} - измеряемый размер; α₁ и α₂ - коэффициенты линейного расширения материалов измерительного средства и изделия; t₁ и t₂ - температуры измерительных средств и изделия.

Дополнительную погрешность нормируют в виде коэффициента, указывающего «на сколько» или «во сколько» изменяется погрешность при отклонении номинального значения. Например, указание, что температурная погрешность вольтметра составляет ±1% на 10°С, означает, что при изменении среды на каждые 10°С добавляется дополнительная погрешность 1%.

Таким образом, повышение точности измерения размеров добиваются за счет уменьшения влияния отдельных погрешностей на результат измерения. Например, нужно выбирать наиболее точные приборы, устанавливать их на ноль (размер) по концевым мерам длины высокого разряда, поручать измерения опытным специалистам и т.д.

Статические погрешности являются постоянными, не изменяющимися в процессе измерения, например неправильная установка начала отсчета, неправильная настройка СИ.

Динамические погрешности являются переменными в процессе измерения; они могут монотонно убывать, возрастать или изменяться периодически.

На каждое средство измерений погрешность приводится только в какой-то одной форме.

Если погрешность СИ при неизменных внешних условиях постоянна во всем диапазоне измерений (задается одним числом), то

D = ± а. (1.9)

Если погрешность меняется в указанном диапазоне (задается линейной зависимостью), то

D = ± (а + bx) (1.10)

При D = ± а погрешность называется аддитивной, а при D =± (а+bx) – мультипликативной.

Если погрешность выражается в виде функции D = f(x), то она называется нелинейной.

Дата добавления: 2014-01-04