Уравнение затухающих колебаний

Задачи

1. Определить период колебаний железнодорожной платформы массой 20 т относительно горизонтальной оси, если платформа одним краем висит на упоре. Коэффициент упругости подвески 1·10⁷ Н/м

2. Определить период галопирующих колебаний двухосного вагона массой 40 т, если расстояние между осями 10 м. Коэффициент упругости одной пружины 2·10⁷ Н/м, длина вагона 15 м.

3. Тяговый двигатель при опорно-осевом подвешивании с моментом инерции 50 кг м² подвешен к раме вагона на пружине, коэффициент упругости которой 2·10⁵ Н/м. Определить частоту собственных колебаний двигателя, если расстояние от оси до пружины 0,4 м.

4. При подвешивании тягового двигателя массой 500 кг к раме вагона пружины подвески растянулись на 0,5 см. Определить период колебаний двигателя.

5. На платформу массой 20 т опустился контейнер массой 5 т со скоростью 1м/с. Определить амплитуду и период вертикальных колебаний платформы. Коэффициент упругости пружин подвески 1·10 ⁷ Н/м.

6. Платформа массой 40 т при движении совершает вертикальные колебания с частотой 2 Гц и амплитудой 1 см. Определить наибольшую скорость и ускорение колебаний платформы. Определить наибольшую и наименьшую силы давления вагона на рельсы.

7. Определить амплитуду и период горизонтальных колебаний вагона массой 60 т на пружине автосцепки, если вагон на скорости 0,5 м/с сцепился с таким же вагоном. Коэффициент упругости пружин автосцепки 2·10⁵ Н/м. Трением пренебречь.

15. ЗАТУХАЮЩИЕ КОЛЕБАНИЯ

Затухающие колебания – это собственные колебания маятников, амплитуда которых со временем уменьшается. Реально собственные колебания всегда затухающие из-за действия силы сопротивления среды.

Получим уравнение затухающих колебаний. На маятник действует, во-первых, упругая возвращающая сила. В первом приближении силы упругости пропорциональны смещению х от положения равновесия где 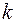– коэффициент упругости. Во-вторых, сила сопротивления среды. Примем, что сила сопротивления пропорциональна скорости . Так бывает при движении тела в вязкой среде с небольшой скоростью.

Уравнение второго закона Ньютонав проекции на ось Ох будет иметь вид: произведение массы тела на ускорение равно сумме проекций сил упругости и сопротивления:

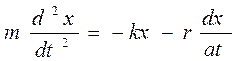. (15.1)

Приведём это уравнение к канонической форме, поделив его на массу

. (15.2)

Здесь обозначено: – коэффициент затухания, 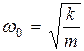– циклическая частота свободных (незатухающих) колебаний.

Решением этого дифференциального уравнения является функция, превращающая уравнение в тождество

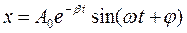, (15.3)

где 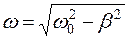– циклическая частота затухающих колебаний, – амплитуда колебаний в начальный момент времени, – начальная фаза колебаний. При малом затухании (b < w₀) частота затухающих колебаний практически не отличается от частоты свободных колебаний. Если b > w₀, то колебания невозможны: тело, выведенное из положения равновесия, медленно смещается к положению равновесия. Такое движение называется апериодическим колебанием.

Амплитудой затухающих колебаний является выражение перед синусом в уравнении (15.3)

А =А ₀ е ^{-b t}. (15.4)

Как видно, со временем амплитуда уменьшается по экспоненциальному закону (рис. 15.1, пунктир).

Дата добавления: 2014-01-04