Уравнение вынужденных колебаний

Задачи

1. Амплитуда вертикальных колебаний вагона массой 60 т за три секунды уменьшилась в два раза. Определить коэффициент сопротивления амортизаторов.

2. Амплитуда вертикальных колебаний вагона массой 60 т за три колебания уменьшилась в 2,72 раза. Определить коэффициент сопротивления амортизаторов, если коэффициент упругости пружин подвески 2·10⁷ Н/м.

3. Определить импульс силы удара и силу удара, полученного колесом при накатывании ползуна длиной 16 мм на рельс со скоростью 20 м/с. Диаметр колеса 1,02 м, масса колеса 800 кг. Во сколько раз сила действия пружины подвески на вагон меньше силы удара стыка рельсов на колесо, если период колебаний колеса относительно вагона 0,2 с.

4. Определить амплитуду силы давления пружины подвески на вагон, если колесо массой 800 кг и со скоростью 20 м/с наезжает на стык рельса с ударом. Отношение ширины стыка к радиусу колеса 1/50. Период собственных колебаний колеса относительно вагона 0,2 с.

5. Определить, при каком минимальном значении коэффициента сопротивления амортизаторов вагона массой 40 т, вагон после смещения внешним воздействием без колебаний стремится к положению равновесия (апериодическое колебание).

6. Время релаксации колебаний вагона 3 с. Определить относительные потери энергии за одно колебание. Масса вагона 40 т, коэффициент упругости пружин подвески 2·10⁷ Н/м.

7. Вертикальные колебания вагона массой 40 т происходят по закону 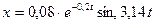. Определить коэффициент упругости рессор вагона, через сколько колебаний энергия колебаний уменьшится в 10 раз.

16. ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ

Если маятник отвести от положения устойчивого равновесия и отпустить, то он начнет совершать собственные затухающие колебания под действием упругой силы и силы сопротивления. Будем считать, что упругая сила пропорциональна смещению F_упр = −kx, а сила сопротивления пропорциональна скорости движения 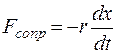. Здесь 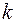и r – коэффициенты упругости и сопротивления. Если кроме этого приложить к маятнику еще внешнюю периодическую силу 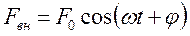, то он будет совершать вынужденные колебания.

Получим формулу для амплитуды вынужденных колебаний маятника, решив уравнение второго закона Ньютона

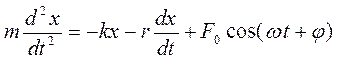. (16.1)

Разделив на массу, приведем уравнение к канонической форме

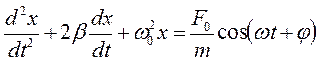, (16.2)

Это дифференциальное уравнение вынужденных колебаний. В нем введены обозначения: 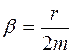– коэффициент затухания, 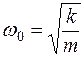– циклическая частота собственных свободных колебаний.

Как показывает опыт, если на маятник начать действовать периодической силой, то вынужденные колебания устанавливаются не сразу. В течение некоторого времени на вынужденные колебания накладываются собственные колебания. Но так как собственные колебания являются затухающими, то со временем они исчезают и маятник совершает только вынужденные колебания. Их частота равна частоте внешней периодической силы. Поэтому частное решение уравнения (16.2) будем искать для установившихся вынужденных колебаний в виде

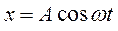, (16.3)

где 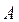– амплитуда колебаний, наибольшее смещение маятника от положения равновесия. Чтобы убедиться, что функция (16.3) является решением, следует подставить ее и первую, вторую производные в уравнение (16.2)

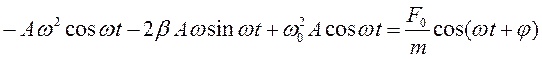. (16.4)

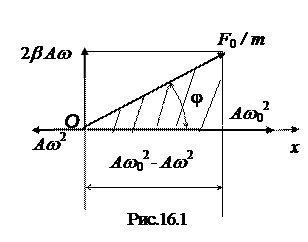
Это уравнение содержит две неизвестные величины: амплитуду колебаний А и сдвиг фаз между силой и смещением 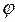. Для их определения воспользуемся заменой тригонометрического уравнения его геометрическим представлением в виде векторной диаграммы (рис. 16.1).

Для этого из полюса О следует провести векторы, длины которых равны амплитудам, а углы относительно полярной оси равны начальным фазам. Теперь, если вращать векторы вокруг полюса О против часовой стрелки с угловой скоростью, равной частоте ω, то их проекции будут равны членами уравнения (16.4).

На векторной диаграмме сумма векторов, изображающих слагаемые в левой части уравнения должна быть равна вектору, изображающему правую часть уравнения (16.4). Запишем теорему Пифагора для заштрихованного треугольник

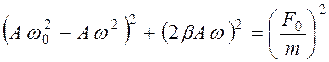. (16.5)

Отсюда получим уравнение для амплитуды вынужденных колебаний

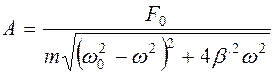. (16.6)

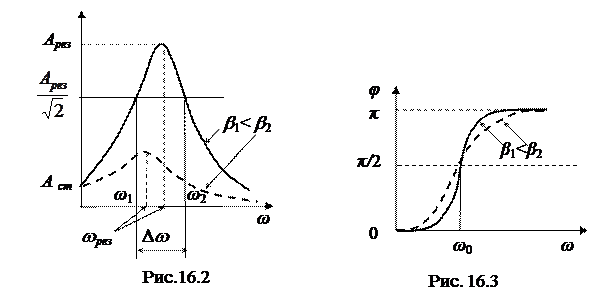
С ростом частоты амплитуда сначала возрастает от величины статического смещения 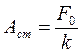, достигает наибольшего значения и затем снова уменьшается (рис. 16.2). Сильное увеличение амплитуды вынужденных колебаний при некоторой частоте называется резонансом. Чтобы получить условие резонанса, следует, как при поиске максимума функции, приравнять производную от подкоренного выражения (16.6) к нулю. Откуда получим 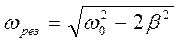. Как видно, резонанс наступает при частоте вынуждающей силы, близкой к частоте свободных колебаний. Подставив частоту резонанса в формулу (16.6), получим для амплитуды резонанса

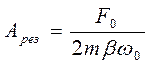. (16.7)

Резонанс обусловлен тем, что направление скорости тела и направление силы совпадают в течение всего периода колебания. Поэтому отбор мощности от источника (N=F∙V) оказывается наибольший. Чем меньше сопротивление среды (β → 0), тем выше амплитуда при резонансе.

По резонансной кривой можно определить коэффициент затухания. Проведем на уровне 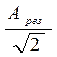горизонтальную линию (рис. 16.2). Абсциссы точек пересечения определим, подставив в левую часть уравнения (16.6) амплитуду при резонансе (16.7), деленную на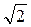. Решив квадратное уравнение относительно корней ω ₁ и ω ₂, получим, что полуширина резонансной кривой Δ ω = ω ₁– ω ₂ равна коэффициенту затухания: .

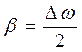Сдвиг фаз между силой и смещением можно определить из треугольника векторной диаграммы (рис. 16.1)

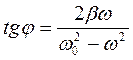. (16.8)

При малых частотах вынуждающей силы (ω <<ω ₀), сила и смещение почти совпадают по фазе. При резонансе сдвиг фаз возрастает до 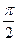, сила и скорость совпадают по направлению. При высоких частотах сила и смещение находятся в противофазе (рис. 16.3)

.

Дата добавления: 2014-01-04