Поле сферического конденсатора

Обкладками сферического конденсатора являются две концентрические сферы (R ₁ и R ₂). Сообщим этим поверхностям одинаковые по величине, но разноимённые заряды +q и –q и вычислим электрическое поле, создаваемое этими зарядами в пространстве (рис. 2.10.).

Сферы делят пространство на 3 области:

I — внутри первой сферы (r ₁ < R ₁),

II — между обкладками (R ₁ £ r ₂ < R ₂),

III — за пределами конденсатора (r ₃ > R ₂).

Рис. 2.10.

Область I.

Выберем замкнутую гауссову поверхность внутри первой области. Разумно, руководствуясь соображениями симметрии, эту поверхность выбрать сферической (r ₁).

Поток вектора напряжённости через эту поверхность (по определению потока) равен:

Этот поток, согласно теореме Гаусса, пропорционален заряду, заключённому внутри поверхности. Но внутри сферы радиуса r ₁ заряд отсутствует. Поэтому и поток равен нулю

(!)

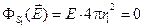Отсюда заключаем, что в области I поле равно нулю

0 < r < R ₁, E = 0 (2.18)

Область II.

Вновь в качестве замкнутой поверхности выберем сферу, но теперь её радиус r₂ лежит в пределах от R ₁ до R ₂.

Вычислим поток вектора напряжённости поля через эту гауссову поверхность.

Воспользуемся теорией Гаусса: :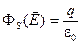

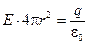
Оказывается, что электрическое поле между обкладками сферического конденсатора неотличимо от поля точечного заряда

. (2.19)

Посмотрим теперь, как выглядит поле в области III.

Вновь выберем замкнутую гауссову сферическую поверхность (радиус r ₃ > R ₂). Вычисляем поток вектора напряжённости

Этот поток равен нулю, так как он пропорционален алгебраической сумме зарядов, заключённых внутри этой поверхности. Но алгебраическая сумма одинаковых разноимённых зарядов равна нулю

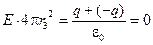
Отсюда следует, что Е = 0 (r ₃ ³ R ₂)/

График Е = Е (r) приведён на рисунке 2.11.

Рис. 2.11.

Лекция 3 «Потенциал электростатического поля»

План лекции

3.1. Работа сил электростатического поля при перемещении заряда. Потенциал и разность потенциалов.

3.2. Теорема о циркуляции вектора напряжённости электростатического поля.

3.3. Связь напряжённости и потенциала электростатического поля.

3.4. Примеры расчёта потенциала электростатического поля.

3.4.1. Потенциал поля точечного заряда.

3.4.2. Разность потенциалов на обкладках сферического конденсатора.

Существуют две характеристики электрического поля. В любой точке пространства поле можно задать либо вектором напряжённости — это «силовая» характеристика поля, либо потенциалом — это его энергетическая характеристика.

Потенциал — энергетическая характеристика поля, связанная и с энергией заряда в электростатическом поле и с работой, совершаемой электрической силой при перемещении заряда.

Дата добавления: 2014-01-04