Правила Кирхгофа. Рассмотренные нами законы постоянного тока позволяют рассчитать токи в сложных разветвлённых электрических цепях

Рассмотренные нами законы постоянного тока позволяют рассчитать токи в сложных разветвлённых электрических цепях. Эти расчёты упрощаются, если пользоваться правилами Кирхгофа.

Правил Кирхгофа два: правило токов и правило напряжений.

Правило токов относится к узлам цепи, то есть, к таким точкам схемы, где сходятся не менее трёх проводников (рис. 7.4.). Правило токов гласит: алгебраическая сумма токов в узле равняется нулю:

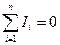. (7.9)

Рис. 7.4.

При составлении соответствующего уравнения, токи, втекающие в узел, берутся со знаком плюс, а покидающие его — со знаком минус. Так, для узла А (рис. 7.3.) можно записать:

I ₁ – I ₂ – I ₃ + I ₄ – I ₅ = 0.

Это первое правило Кирхгофа является следствием уравнения непрерывности (см. (6.7)) или закона сохранения электрического заряда.

Правило напряжений относится к любому замкнутому контуру разветвлённой цепи.

Выделим, например, в разветвлённой сложной цепи замкнутый элемент 1-2-3-1 (рис. 7.5.). Произвольно обозначим в ветвях контура направления токов I ₁, I ₂, I ₃. Для каждой ветви запишем уравнение закона Ома для неоднородного участка цепи:

Участок .

Здесь R ₁, R ₂, R ₃ — полное сопротивление соответствующих ветвей. Сложив эти уравнения, получим формулу второго правила Кирхгофа:

I ₁ R ₁ – I ₂ R ₂ – I ₃ R ₃ = e₁ + e₂ – e₃ – e₄ + e₅.

Правило напряжений формулируется так: в любом замкнутом контуре алгебраическая сумма падений напряжения равна алгебраической сумме э.д.с., встречающихся в этом контуре:

. (7.10)

Рис. 7.5.

При составлении уравнения (7.10) второго правила Кирхгофа задаются направлением обхода: в нашем примере — по часовой стрелке. Токи, совпадающие с направлением обхода, берутся со знаком плюс (I ₁), токи противоположного направления — со знаком минус (– I ₂, – I ₃).

Э.д.с. источника берётся со знаком плюс, если он создаёт ток, совпадающий с направлением обхода (+e₁, +e₂, +e₅). В противном случае э.д.с. отрицательна (–e₃, –e₄).

В качестве примера составим уравнения правил Кирхгофа для конкретной электрической схемы — измерительного моста Уитстона (рис. 7.6.). Мост образуют четыре резистора R ₁, R ₂, R ₃, R ₄. В точках A и B к мосту подключен источник питания (e, r), а в диагонали BD — измерительный гальванометр с сопротивлением R _g.

Рис. 7.6.

1) Во всех ветвях схемы произвольно обозначим направления токов I ₁, I ₂, I ₃, I ₄, I _g, I _e.

2) В схеме четыре узла: точки A, B, C, D. Для трёх из них составим уравнения первого правила Кирхгофа — правила токов:

точка А: I _e – I ₁ – I ₄ = 0; (1)

точка B: I ₁ – I ₂ – I _g = 0; (2)

точка D: I ₄ + I _g – I ₃ = 0. (3)

3) Для трёх контуров цепи ABDA, BCDB и ADC e A составим уравнения второго правила Кирхгофа. Во всех контурах направление обхода по часовой стрелке.

ABDA: I ₁ R ₁ + I _g R _g – I ₄ R ₄ = 0; (4)

BCDB: I ₂ R ₂ – I ₃ R ₃ – I _g R _g = 0; (5)

ADC e A: I ₄ R ₄ + I ₃ R ₃ + I _e r = e. (6)

Таким образом, мы получили систему шести уравнений, решая которую можно найти все шесть неизвестных токов.

Но чаще мост Уитстона используется для измерения неизвестного сопротивления R_x º R ₁. В этом случае резисторы R ₂, R ₃ и R ₄ — переменные. Меняя их сопротивления, добиваются того, чтобы ток в измерительной диагонали моста оказался равным нулю I _g = 0. Это означает, что:

I ₁ = I ₂ см. (1),

I ₃ = I ₄ см. (3),

I ₁ R ₁ = I ₄ R ₄ см. (4),

I ₂ R ₂ = I ₃ R ₃ см. (5).

Учитывая эти упрощающие обстоятельства, приходим к выводу, что:

,

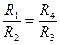или:

.

Замечательно, что для определения неизвестного сопротивления нужно знать лишь сопротивления резисторов моста R ₂, R ₃ и R ₄. Э.д.с. источника, его внутреннее сопротивление, как и сопротивление гальванометра при таком измерении не играют никакой роли.

Дата добавления: 2014-01-04