Собственные затухающие колебания

Собственные затухающие колебания происходят в колебательном контуре RLC (рис. 11.1. и 11.5.).

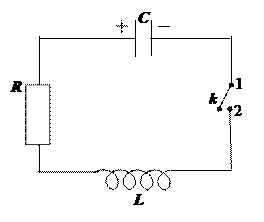
Рис. 11.5.

Эти колебания можно описать следующим дифференциальным уравнением (правило напряжений Кирхгофа):

IR – U _C = e^СИ. (11.6)

Здесь по-прежнему: I = ; U _C = ; e^СИ = = = .

Учитывая эти соотношения, уравнению (11.6) придадим следующий вид:

;

. (11.7)

Здесь d = 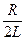— коэффициент затухания; = 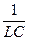— частота собственных незатухающих колебаний.

Уравнение (11.7) — дифференциальное уравнение собственных затухающих электрических колебаний.

Если в системе 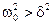, то решением этого уравнения является следующая функция:

q = Ae ^–dtcos(w t + j). (11.8)

Здесь А и j — постоянные, которые можно найти, воспользовавшись начальными условиями, а частота колебаний:

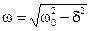. (11.9)

Убедиться в том, что функция (11.8) действительно является решением дифференциального уравнения (11.7), каждый может самостоятельно, подставив (11.8) в (11.7).

Важной характеристикой затухающего процесса является логарифмический декремент затухания — логарифм отношения амплитуд двух соседних колебаний (рис. 11.2 б):

. (11.10)

Логарифмический декремент затухания равен произведению коэффициента затухания d на время одного полного колебания (период) Т.

Процесс затухания колебания до нуля продолжается бесконечное время, поэтому условно принято считать, что процесс затух, если амплитуда колебаний уменьшилась в е раз.

Вычислим, сколько же колебаний N_e произойдёт, пока амплитуда уменьшится в е раз?

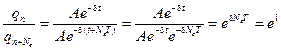
Отсюда следует, что d N_eT = N_e × d = 1.

Ил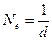и:

и .

Логарифмический декремент затухания d обратен числу колебаний, по истечению которых амплитуда падает в е раз.

В радиотехнике для энергетической характеристики затухания часто используют величину, которая получила название добротность контура:

. (11.11)

Покажем, что добротность с точностью до 2p равна отношению энергии Е, запасенной в контуре, к убыли энергии за один период (–D Е):

.

Энергия, запасенная в контуре, пропорциональна квадрату амплитуды заряда конденсатора:

.

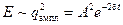Относительная убыль энергии за период равна:

.

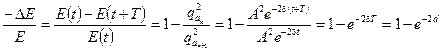При малом затухании (когда d << 1) можно приблизительно принять, что:

e ^{–2 d} = 1 – 2 d.

Тогда относительная убыль энергии:

,

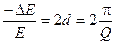или

. (11.12)

Мы рассмотрели затухающие колебания при малом затухании, когда .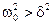

Если затухание столь значительно, что d² ³ , то в этом случае вместо колебательного процесса происходит апериодический разряд конденсатора (рис. 11.2. г). Переход от периодического к апериодическому разряду происходит при критическом сопротивлении R _к, которое можно найти из условий апериодичности:

;

;

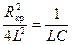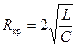. (11.13)

Величина критического сопротивления зависит только от величины индуктивности и ёмкости колебательного контура.

Дата добавления: 2014-01-04