Вынужденные колебания. Резонанс

Индуктивность в цепи переменного тока (рис. 11.9.)

Резистор (R) в цепи переменного тока (рис. 11.7.)

Рис. 11.7.

При протекании переменного тока I = I ₀cosw t, падение напряжения на резисторе будет меняться по гармоническому закону:

U_R = I × R = I ₀ R cosw t. (11.15)

Причём колебания тока и напряжения будут происходить синфазно (рис. 11.7.).

3.2. Ёмкость в цепи переменного тока I = I₀coswt (рис. 11.8.)

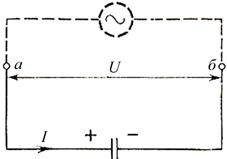
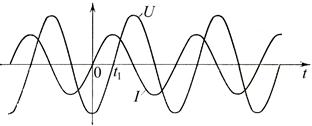
Рис. 11.8.

Вычислим напряжение на конденсаторе при течении в цепи переменного тока (рис. 11.8.):

. (11.16)

Напряжение на конденсаторе колеблется с той же частотой, что и ток, но по фазе ток в конденсаторе на опережает напряжение.

Рис. 11.9.

В катушке действует э.д.с. самоиндукции, поэтому закон Ома для неоднородного участка цепи запишем так:

U = Ir – e^СИ.

Здесь сопротивление идеальной катушки индуктивности r = 0; e^СИ = — э.д.с. самоиндукции. Тогда:

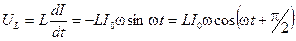. (11.17)

Напряжение на катушке индуктивности на опережает по фазе ток (рис. 11.9.).

Вернёмся к уравнению вынужденных колебаний (11.14):

U_R + U_C + U_L = U ₀cosw t.

Теперь мы знаем, что здесь:

U_R = I ₀ R cosw t;

;

.

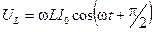Сложим эти три гармонические колебания, воспользовавшись методом векторных диаграмм (рис. 11.10.). Для этого выберем ось тока (I). U_R представим вектором, совпадающим по направлению с направлением оси тока. Напряжения U_C и U_L будут представлены векторами, повёрнутыми относительно оси тока на и соответственно.

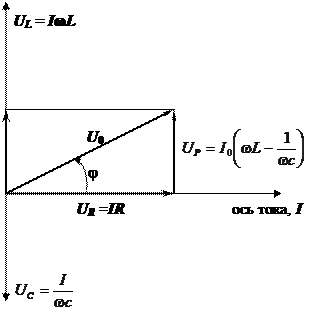
Рис. 11.10.

Сложение трёх колебаний заменим теперь сложением этих трёх векторов.

Сумма падений напряжений на индуктивности и ёмкости определит реактивную составляющую полного напряжения — U _р.

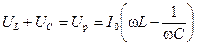. (11.18)

Амплитуда этого напряжения, как следует из (11.18) пропорциональна амплитуде тока.

Рассматривая последнее уравнение, как запись закона Ома, можно коэффициент пропорциональности между током и напряжением назвать сопротивлением этого участка.

R _p= 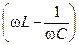— реактивное сопротивление контура.

Продолжим сложение векторов и к уже полученной сумме прибавим вектор, изображающий U_R = I ₀ R.

Результатом сложения всех трёх колебаний (векторов) будет напряжение U = U ₀cosw t, поддерживающее вынужденные колебания в контуре (см. 11.4).

Как следует из векторной диаграммы, амплитуда этого напряжения равна:

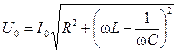. (11.19)

Или амплитуда тока в цепи:

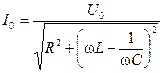. (11.20)

При этом ток будет запаздывать по фазе от напряжения на j:

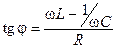. (11.21)

Уравнения (11.19) и (11.20) иногда называют законом Ома для переменного тока. Но надо иметь в виду, что эти формулы связывают только амплитудные значения тока I ₀ и напряжения U ₀.

В уравнении (11.21) — полное сопротивление колебательного контура, складывающееся из активного (R) и реактивного 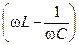сопротивлений.

Теперь проанализируем полученные результаты (11.20) и (11.21).

Пусть в колебательном контуре RLC (рис. 11.6.) действует источник переменного напряжения:

U = U ₀cosw t.

Теперь мы уже знаем, что в контуре установятся гармонические колебания тока:

I = I ₀cos(w t – j).

Амплитуда этого колебания прямо пропорциональна амплитуде приложенного напряжения U ₀ и обратно пропорциональна полному сопротивлению контура:

.

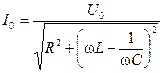Ток будет отставать по фазе от напряжения на угол j:

.

Будем теперь менять частоту w возбуждающего сигнала, оставляя его амплитуду U ₀ неизменной.

При w = 0, I (w = 0) = 0. Это легко понять: ведь сопротивление колебательного контура, с его ёмкостью С, бесконечно для постоянного тока (R_C = = ¥ при w = 0). Отсюда и нулевой ток.

Ток будет стремиться к нулю и в случае неограниченного роста частоты колебаний. При w ® ¥, R_L = w L ® ¥ и I ® 0.

В промежутке между этими предельными значениями частоты, амплитуда тока проходит через максимум. Резонансные кривые для амплитуды силы тока I ₀ = I ₀(w) приведены на рис. 11.11.

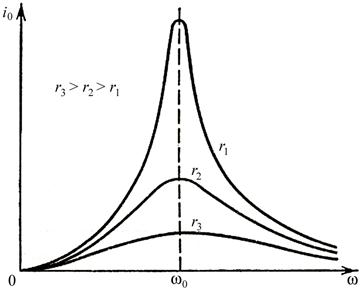
Рис. 11.11.

Амплитуда I ₀ достигает максимума, когда реактивное сопротивление контура становится равным нулю:

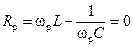. (11.22)

При этой (резонансной) частоте сопротивление контура будет определяться только сопротивлением резистора R:

(11.23)

Из (11.22) следует, что резонанс тока наступает при частоте w_P = w₀, равной частоте собственных незатухающих колебаний контура:

.

Понятно, что уровень резонансного максимума амплитуды тока зависит от величины активного сопротивления контура (11.23).

Анализ зависимости фазового сдвига j от частоты приводит к выводу, который графически представлен на рис 11.12.

Рис. 11.12.

Наибольший интерес представляет момент резонанса, когда частота вынуждающего сигнала равна частоте w₀. Тогда амплитуда тока достигает своего максимума, а разность фаз между током и приложенным напряжением равна нулю (j = 0).

Контур в этом случае выступает как чисто активное сопротивление.

Этот важный частный случай вынужденных колебаний называется резонансом напряжений. Именно резонанс напряжений используется в радиотехнике при настройке на сигнал строго определённой частоты.

Дата добавления: 2014-01-04