Принцип суперпозиции электростатических полей, Поле диполя

Рассмотрим метод определения значения и направления вектора напряженности Е в каждой точке электростатического поля, создаваемого системой неподвиж­ных зарядов q ₁, q ₂,..., Q_n.

Опыт показывает, что к кулоновским силам применим рассмотренный в механи­ке принцип независимости действия сил (см. §6), т.е. результирующая сила F, действующая со стороны поля на пробный заряд Q ₀, равна векторной сумме сил F _i, приложенных к нему со стороны каждого из зарядов Q_i:

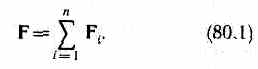
Согласно (79.1), F =Q₀ E и F _i,=Q₀ E _i, где Е —напряженность результирующего по­ля, а Е _i — напряженность поля, создавае­мого зарядом Q _i. Подставляя последние выражения в (80.1), получим

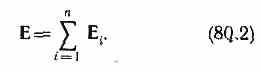
Формула (80.2) выражает принцип су­перпозиции (наложения) электростатиче­ских полей, согласно которому напряжен­ность Е результирующего поля, создавае­мого системой зарядов, равна геометриче­ской сумме напряженностей полей, со­здаваемых в данной точке каждым из зарядов в отдельности.

Принцип суперпозиции позволяет рас­считать электростатические поля любой системы неподвижных зарядов, поскольку если заряды не точечные, то их можно всегда свести к совокупности точечных зарядов.

Принцип суперпозиции применим для расчета электростатического поля элек­трического диполя. Электрический ди­поль — система двух равных по модулю разноименных точечных зарядов (+ Q, - Q), расстояние l между которыми зна­чительно меньше расстояния до рассмат­риваемых точек поля. Вектор, направлен­ный по оси диполя (прямой, проходящей через оба заряда) от отрицательного за­ряда к положительному и равный расстоя­нию между ними, называется плечом дипо­ля l. Вектор

совпадающий по направлению с плечом диполя и равный произведению заряда

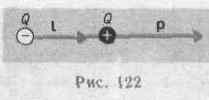
|Q| на плечо l, называется электрическим моментом диполя р или дипольным мо­ментом (рис. 122).

Согласно принципу суперпозиции (80.2), напряженность Е поля диполя в произвольной точке

Е = Е ₊ + Е _-,

где Е ₊ и Е _- — напряженности полей, со­здаваемых соответственно положительным и отрицательным зарядами. Воспользо­вавшись этой формулой, рассчитаем на­пряженность поля на продолжении оси диполя и на перпендикуляре к середине его оси.

1. Напряженность поля на продолже­нии оси диполя в точке А (рис. 123). Как видно из рисунка, напряженность поля диполя в точке А направлена по оси дипо­ля и по модулю равна

Е_A=Е₊-Е_-.

Обозначив расстояние от точки А до середины оси диполя через л, на основании формулы (79.2) для вакуума можно за­писать

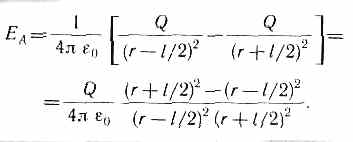
Согласно определению диполя, l /2<<r, по­этому

2. Напряженность поля на перпенди­куляре, восставленном к оси из его середи­ны, в точке В (рис. 123). Точка В равноу­далена от зарядов, поэтому

где r' — расстояние от точки В до середи­ны плеча диполя. Из подобия равнобед-

ренных треугольников, опирающихся плечо диполя и вектор ев, получим

откуда

Е_B=Е₊l/r'. (80.5)

Подставив в выражение (80.5) значение (80.4), получим

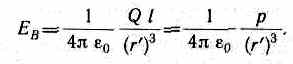
Вектор Е _B имеет направление, противопо­ложное электрическому моменту диполя (вектор р направлен от отрицательного заряда к положительному).

Дата добавления: 2014-01-04