СРС Вычисление разности потенциалов по напряженности поля

Установленная в § 85 связь между напря­женностью поля и потенциалом позволяет по известной напряженности поля найти разность потенциалов между двумя про­извольными точками этого поля.

1. Поле равномерно заряженной бесконеч­ной плоскости определяется формулой (82.1): E=s/(2e₀), где s — поверхностная плотность заряда. Разность потенциалов между точками, лежащими на расстояниях х ₁, и x₂ от плоскости

(используем формулу (85.1)), равна

2. Поле двух бесконечных параллельных разноименно заряженных плоскостей определя­ется формулой (82.2): Е=s/e ₀, где s — повер­хностная плотность заряда. Разность потенциа­лов между плоскостями, расстояние между ко­торыми равно d (см. формулу (85.1)), равна

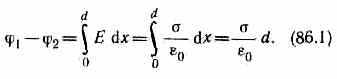
3. Поле равномерно заряженной сфериче­ской поверхности радиуса R с общим зарядом Q вне сферы (r>R) вычисляется по (82.3):

E=(1/4pe₀)Q/r². Разность потенциалов между двумя точками, лежащими на расстояниях r ₁ и r ₂ от центра сферы (r ₁ >R, r ₂> R), равна

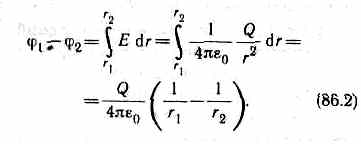
Если принять r ₁ =r и r ₂=¥, то потенциал поля вне сферической поверхности, согласно формуле (86.2), задается выражением

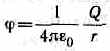
(ср. с формулой (84.5)). Внутри сферической поверхности потенциал всюду одинаков и равен

График зависимости j от r приведен на рис. 134.

4. Поле объемно заряженного шара ра­диуса R с общим зарядом Q вне шара (r>R) вычисляется по формуле (82.3), поэтому раз­ность потенциалов между двумя точками, лежа­щими на расстояниях r ₁ и r ₂ от центра шара (r ₁ >R, r ₂ >R), определяется формулой (86.2). В любой точке, лежащей внутри шара на рас­стоянии r' от его центра (r'<R), напряжен­ность определяется выражением (82.4): E =(1/4pe₀)(Q/R³)r'. Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r '₁ и r '₂ от центра шара (r' ₁ <R, r' ₂< R), равна

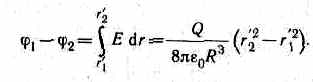
5. Поле равномерно заряженного бесконеч­ного цилиндра радиуса К, заряженного с линей­ной плотностью т, вне цилиндра (r>R) опреде­ляется формулой (82.5): E=(1/2pe₀)(t/r). Следовательно, разность потенциалов между двумя точками, лежащими на расстояниях r ₁ и r ₂ от оси заряженного цилиндра (r ₁ >R, r ₂> R), равна

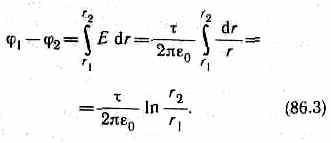
Дата добавления: 2014-01-04