Уравнение Бернулли

Основным количественным соотношением, описывающим течение идеальной (то есть абсолютно несжимаемой и невязкой) жидкости яв­ляется уравнение Бернулли, вытекающее из закона сохранения энергии в движущейся жидкости.Для его установления расс­мотрим трубку тока идеальной жидкости, в которой выделим два сечения площадью S₁ и S₂ (рис.4). Пусть центры этих сечений расположены на высотах h₁ и h₂, отсчитываемых от некоторого уровня. Линейные скорости час­тиц жидкости в этих сечениях обозначим v ₁ и v ₂. Силы, обус­лавливающие течение жидкости, оказывают давление Р₁ и Р₂ на торцах объема жидкости между выделяемыми сечениями S₁ и S₂. При стационарном течении идеальной жидкости ее полная энергия в местах расположения выделенных сечений сохраняется, следователь­но:

m v ₁² / 2 + Р₁V + mgh₁ = m v ₂² / 2 + P₂V + mgh₂. (2)

В уравнении (2) m - одинаковая масса жидкости объема V, протекаю­щей через сечения S₁ и S₂. Первые слагаемые в обоих частях равенс­тва представляют кинетическую энергию жидкости, вторые - потенци­альную энергию давления, третьи - потенциальную энергию, обуслов­ленную расположением жидкости на высотах h₁ и h₂.

Разделив правую и левую часть соотношения (2) на объем жид­кости V и, вводя плотность жидкости r, получим:

r v ₁²/2+P₁+rgh₁ = r v ₂²/2+P₂+rgh₂ или r v ²/2+P+rgh = const. (3)

Формула (3) называется уравнением Бернулли, утверждающим, что сумма разнопричинных давлений в жидкости (полное давление) являет­ся постоянной величиной. Слагаемое r v ²/2 представляет динамическое давление, обусловленное движением жидкости; Р - статическое давле­ние, не связанное с движением жидкости (оно может быть измерено, например, манометром, движущимся вместе с жидкостью); rgh - весо­вое (гидростатическое) давление.

Рассмотрим некоторые следствия, вытекающие из уравнения Бер­нулли:

а) Способ измерения скорости движения жидкости.

Представим, что в движущуюся жидкость опущены две трубки ма­лого сечения, причем, плоскость поперечного сечения одной из них параллельна направлению скорости движения жидкости v, а другая (трубка Пито) изогнута так, что плоскость сечения изогнутой части перпендикулярна направлению скорости течения (рис.5). Подъем жидкости в прямой трубке на высоту h₁ обусловлен лишь ста­тическим давлением Р _c, которое можно определить по формуле: P _c = rgh₁. В трубке Пито подъем жидкости на высоту h₂ обуслов­лен полным давлением Р _п - в данном случае суммой статичес­кого Р _с и динамического Р _д дав­лений (течение происходит горизонтально и весовое давление не учитывается). Следовательно:

Р _п = Р _с + Р _д; rgh₂ = rgh₁ + r v ²/2 (4)

Из формулы (4) находим линейную скорость жидкости:

v = . (5)

Таким образом, по измеренной разности уровней жидкости в пря­мой и изогнутой трубках определяется скорость течения жидкости.

б) Всасывающее действие струи.

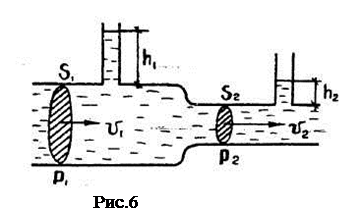
Рассмотрим течение жидкости по горизонтальной трубе перемен­ного сечения. Выделим два участка с площадью поперечного сечения S₁ и S₂, причем, для определенности, S₁>S₂ (рис.6).Запишем для данного случая уравнение Бернулли:

r v ₁² / 2 + P₁ = r v ₂²/2 + P₂ , (6)

где v ₁ и v ₂ – скорости течения жидкости в се­чениях S₁ и S₂. Стати­ческие давления Р₁ и Р₂ в соответствующих сече­ниях могут быть опреде­лены по высотам подъема жидкости h₁ и h₂ в ка­пиллярных трубках. Поскольку S₁ > S₂, то v ₁< v ₂, - в узких местах жидкость течет быстрее. Тогда из уравнения (6) следует, что Р₁ > Р₂, т.е. статическое давление в более широкой части трубки большее, чем в ее узкой час­ти. Если сужение значительно, то скорость жидкости в нем v ₂ намно­го превышает v ₁, статическое давление Р₂ резко уменьшается и может стать ниже атмосферного. В этом случае воздух (или окружающая трубку другая среда) будет засасываться через отверстие в месте расположения сужения. На этом принципе устроены водоструйные насо­сы, ингаляторы, пульверизаторы и др.

в) Закупорка - артерии, артериальный шум.

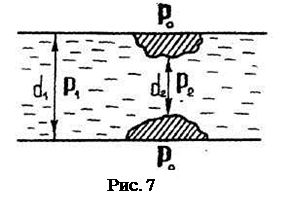
Допустим, что в случае образования атеросклеротической бляш­ки на некотором участке крупной артерии диаметром d₁ возникает су­жение диаметром d₂ (рис.7). Для упрощения будем считать, что арте­рия расположена горизонтально. Рассчитаем тот минимальный диаметр сужения d₂, при котором крово­ток еще возможен, и проанализи­руем явления, возникающие при уменьшении диаметра ниже мини­мального. Течение крови по ар­терии будет происходить до того момента, пока статическое дав­ление Р₂ в месте образования атеросклеротической бляшки бу­дет превышать наружное давление на сосуд Р_o (его можно считать приблизительно равным атмосфер­ному). Итак, кровоток возможен при условии:

Р₂ - Р_o ³ 0. (7)

Чтобы условие (7) было реализовано, диаметр сужения d₂ не должен быть меньше некоторого минимального значения d_min. Этот ми­нимальный просвет сосуда определим, используя уравнение Бернулли уже записанное для этого случая в виде выражения (6), из которого следует:

Р₂ = Р₁ - r ( v ₂² - v ₁²) / 2. (8)

Учтем, что на основании теоремы неразрывности струи

v ₂ =(d₁²/d ²_min) v ₁. (9)

Подставляя теперь формулу (9) в формулу (8) и используя соот­ношение (7), получим уравнение для определения величины d_min:

P₁ - P_o - r v ₁² / 2 [(d₁/d_min) ⁴ - 1] = 0. (10)

Решая уравнение (10) относительно d_min, после элементарных преоб­разований найдем:

d_min = d₁ . (11)

Для оценки численной величины этого минимального диаметра поставим в формулу (11) возможные реальные значения входящих в нее параметров. Возьмем, например, сонную артерию, средний диаметр которой d₁ = 1см, скорость крови v ₁ = 0,2 м/с, плотность крови r =1,05 ×10³ кг/м³. Для нормальных условий разница давлений Р₁ - Р_o = 100 мм.рт.ст.= 1,33 ×10⁴ Па. Тогда вычисления дадут результат: d_min» 2мм.

Представим теперь, что диаметр сужения стал меньше d_min. Тог­да под действием внешнего давления Р_о просвет сосуда в месте рас­положения атеросклеротической бляшки закрывается. Если бы давление Р₁ в незакупоренном участке сосуда оставалось постоянным, то кро­воток был бы полностью остановлен. Однако, в результате работы сердца давление Р₁ начнет возрастать и кровь, все-таки, будет с усилием протекать через сужение. Сердце работает в условиях повы­шенной нагрузки. При прослушивании фонендоскопом наличие этих толчков проявляется в виде прерывистого шума, свидетельствующего о нарушении нормального кровотока.

г) Поведение аневризмы.

Некоторые патологические процессы могут приводить к локально­му снижению прочностных и упругих свойств кровеносных сосудов. В результате на некотором участке сосуда его деформация под действи­ем пульсирующего кровотока становится необратимой - возникает вздутие сосуда (аневризма). Схематически такой сосуд показан на рис 8. Скорость кровотока v ₂ в месте развития аневризмы диаметром d₂ по усло­вию неразрывности струи бу­дет меньше, чем скорость v ₁ в его недеформированной части. На основании уравне­ния Бернулли (6) статичес­кое давление Р₂ в месте вздутия будет больше давления Р₁ на основных участках сосуда нормального сечения. Следовательно, нагрузка на расширенную часть сосуда увеличится и возникшая аневризма под действием повы­шенного давления будет иметь тенденцию к расширению. Разница дав­лений Р₁ - Р₂ может быть рассчитана с использованием формулы (6) для конкретных сосудов. Например, если диаметр сосуда d₁ = 2,5 см, а диаметр аневризмы d₂ = 5см, то добавочное давление Р₂ - Р₁» 0,3 мм.рт.ст. Эта величина мала по сравнению с абсолютным давлением, но, все-таки, даже малое избыточное давление стремится расширить вздутие, что приводит к еще большему замедлению скорости кровотока в деформированной части сосуда и дальнейшему повышению статическо­го давления и т.д. В результате возможен разрыв аневризмы.

Дата добавления: 2014-01-04