Уравнение волны

Механические волны

Механическая волна представляет собой процесс распространения механических колебаний в пространстве. Из-за наличия упругих связей между частицами среды перемещения одной из частиц при возникновении колебаний вызывает движение соседних частиц - этот процесс распространяется в пространстве с некоторой скоростью.

Волна называется продольной, если направление перемещения частиц среды совпадает с направлением распространения волны. Если эти направления взаимно перпендикулярны, то такая волна называется поперечной. Продольные механические волны могут распространяться в любых средах (кроме вакуума), а поперечные - только в твердых телах.

Рассмотренные выше математические выражения, описывающие характер колебаний, определяют смещение как функцию одной переменной - времени. Смещение S в волне зависит уже от двух переменных - времени t и пространственной координаты х - и обладает поэтому двойной периодичностью.

Для получения уравнения волны, то есть аналитического выражения функции двух переменных S = f (t, x), представим что, в некоторой точке пространства возникают гармонические колебания с круговой частотой w и начальной фазой, для упрощения равной нулю (см. рис.8). Смещение в точке М: S_м = A sin w t, где А - амплитуда. Поскольку частицы среды, заполняющие пространство, связаны между собой, то колебания от точки М распространяются вдоль оси х со скоростью v. Через некоторое время D t они достигают точки N. Если в среде отсутсвует затухание, то смещение в этой точке имеет вид: S_N = A sin w (t - D t), т.е. колебания запаздывают на время D t относительно точки M. Поскольку 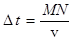, то заменив произвольный отрезок MN координатой х, получим уравнение волны в виде:

(23)

Учитывая, что (где Т - период), а длина волны l = v T, формулу (23) можно записать в виде:

(24) Уравнение волны (23) или (24) позволяет определить в любой момент времени t смещение любой точки, имеющей координату х.

Дата добавления: 2014-01-04