Энтропия и информация

Рассмотрим некоторую систему X, над которой производится измерение, и оценим информацию, получаемую в результате того, что состояние системы X становится полностью известным (погрешность измерений равна нулю). До проведения измерений априорная энтропия системы была Н(Х), после измерений энтропия стала равной нулю, если в результате измерения мы нашли истинное значение величины. Обозначим I_x информацию, получаемую в результате измерений. Она равна уменьшению энтропии I_Х = H(X) – H(X/x_и) = 0 или I_X = H(X), т. е. количество информации, приобретаемое при полном выяснении состояния некоторой физической системы, равно энтропии этой системы.

С учетом формулы (1.24)

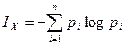(1.26)

где р_i= р(Х Þ x_i). Формула (1.26) означает, что информация I_x есть осредненное по всем состояниям системы значение логарифма вероятности состояния с обратным знаком.

Действительно, для получения I_x каждое значение log p_i,- (логарифм вероятности i-го значения) со знаком минус множится на вероятность этого состояния и все такие произведения складываются. Естественно каждое отдельное слагаемое - log р_i следует рассматривать как частную информацию, получаемую от отдельного измерения, состоящего в том, что система X находится в состоянии Х_i. Обозначим эту информацию I_xi.

I_xi = - log p_i (1.27)

Тогда информация I_x представится как средняя (или полная) информация, получаемая от всех возможных отдельных измерений с учетом их вероятностей.

Так как все числа р_i не больше единицы, то, как частная информация I_xi, так и полная I_x не могут быть отрицательными.

Если все возможные состояния системы одинаково вероятны (p₁ = Р₂= … =р_п=1/п), то частная информация от каждого отдельного измерения I_xi = - log p = log n равна средней (полной) информации

(1.28)

6.3. Применение основных положений теории информации для характеристики процесса измерения

Точность измерений обычно характеризуется числовым значением полученных при измерении или априорно известных погрешностей измерений.

Пусть в результате однократного измерения значения измеряемой величины X результат измерения равен х_и. Если известно, но, что средство измерения имеет случайную абсолютную погрешность в пределах ± D, то не следует утверждать, что действительное значение измеряемой величины равно х_и. Можно лишь утверждать, что это значение лежит в полосе x_и ± D. Незнание истинного значения измеряемой величины сохраняется после получения результата измерения х_и, но теперь оно характеризуется не исходной энтропией Н(Х), а лишь энтропией разброса действительного значения X величины относительно полученного результата x_и. Эта условная энтропия Н(Х/х_и) определяется погрешностью данного средства измерения.

В теории информации факт проведения измерений в диапазоне от Х_н до Х_в означает, что при использовании данного средства измерения может быть получен результат измерений x_и только в пределах от Х_н до Х_в. Другими словами, вероятность получения значений х_и, меньших Х_н и больших Х_в, равна нулю. Вероятность же получения результата х_и в пределах от Х_н до Х_в равна единице.

Если предположить, что плотность распределения различных значений измеряемой величины вдоль всей шкалы средства измерения одинакова, то с точки зрения теории информации наше знание о значении измеряемой величины до измерения может быть представлено графиком

распределения плотности f₁(x) вдоль шкалы значений (рис. 16).

Рис. 16. Плотность распределения данного средства измерения

Поскольку вероятность получения результата измерений x_и в пределах от Х_н до Х_в равна единице, то площадь под кривой f₁ (x) должна быть равна единице. При равномерном распределении плотности вероятности

После проведения измерения из-за наличия погрешности средства измерения (± D) действительное значение измеряемой величины X лежит в пределах от Х_и - D до Х_и + D, т. е. в пределах участка 2D.

С информационной точки зрения интерпретация результата измерения состоит в том, чтобы область неопределенности простиралась от Х_н до X_в и характеризовалась сравнительно небольшой плотностью распределения f₁(x). После измерения неопределенность уменьшилась до величины 2 D, а плотность распределения увеличилась до величины f₂(x) с учетом того, что D << (X_в –X_н), что и отражено на рис. 16.

Получение какой-либо информации об интересующей нас величине заключается в конечном счете в уменьшении неопределенности ее значения.

Определим количество информации в общем случае как

I_x=H(Х)-Н(Х/х_и), (1.29)

где Н(Х) - априорная энтропия; Н(Х/х_и) - условная энтропия.

В нашем примере с равномерным законом распределения

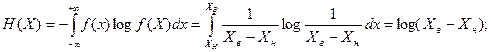
Полученное количество информации

(1.30)

Данная операция, которая обычно используется при определении относительной погрешности измерения, характеризует один из основных приемов анализа информационных свойств измерений.

Глава 7. Организационно-правовые основы метрологической деятельности

Дата добавления: 2014-01-04