
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Современная формулировка
|
|
|
|
Материальные точки взаимодействуют друг с другом силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:

Сила – это количественная мера взаимодействия тел. Сила является причиной изменения скорости тела. В механике Ньютона силы могут иметь различную физическую природу: сила трения, сила тяжести, упругая сила и т. д. Сила является векторной величиной. Векторная сумма всех сил, действующих на тело, называется равнодействующей силой.
Масса – это свойство тела, характеризующее его инертность. При одинаковом воздействии со стороны окружающих тел одно тело может быстро изменять свою скорость, а другое в тех же условиях – значительно медленнее. Принято говорить, что второе из этих двух тел обладает большей инертностью, или, другими словами, второе тело обладает большей массой.
7. Если системы отсчета движутся относительно друг друга равномерно и прямолинейно и в одной из них справедливы законы динамики Ньютона, то эти системы являются инерциальными. Во всех инерциальных системах отсчета законы классической динамики имеют одинаковую форму (инвариантны ); в этом состоит суть механического принципа относительности или принципа относительности Галилея.
8. И́мпульс (Количество движения) — векторная физическая величина, являющаяся мерой механического движения тела. В классической механике импульс тела равен произведению массы m этого тела на его скорость v, направление импульса совпадает с направлением вектора скорости:  .
.
В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости: 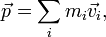
Формула де Бройля связывает импульс и длину волны де Бройля.
Модуль импульса обратно пропорционален длине волны  :
:
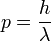
Зако́н сохране́ния и́мпульса (Зако́н сохране́ния количества движения) утверждает, что векторная сумма импульсов всех тел (или частиц) системы есть величина постоянная, если векторная сумма внешних сил, действующих на систему, равна нулю.
Согласно второму закону Ньютона для системы из N частиц:
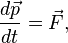
где 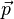 импульс системы,
импульс системы,  — равнодействующая всех сил, действующих на частицы системы.
— равнодействующая всех сил, действующих на частицы системы.
9. Механическая энергия — это энергия, связанная с движением объекта или его положением, способность совершать механическую работу.
В физике механи́ческая эне́ргия описывает сумму потенциальной и кинетической энергий, имеющихся в компонентах механической системы.
Закон сохранения механической энергии утверждает, что если тело или система подвергается действию только консервативных сил, то полная механическая энергия этого тела или системы остаётся постоянной. В изолированной системе, где действуют только консервативные силы, полная механическая энергия сохраняется.
Механическая работа — это физическая величина, являющаяся скалярной количественной мерой действия силы или сил на тело или систему, зависящая от численной величины, направления силы (сил) и от перемещения точки (точек) тела или системы. A=F*S
Кинети́ческая эне́ргия — энергия механической системы, зависящая от скоростей движения её точек.
Wк= mas= 1/2mu2
Изменение величины скорости от u1 до u2 приводит к изменению кинетической энергии, которое записывается в виде:
ΔWк=m/2(u22−u12)
Если u2 < u1, то выражение в скобках отрицательно, ΔWк<0, т.е. тело отдает свою кинетическую энергию.
Потенциальная энергия 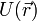 — скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы. Единицей измерения энергии в СИ является Джоуль.
— скалярная физическая величина, характеризующая способность некоего тела (или материальной точки) совершать работу за счет своего нахождения в поле действия сил. Другое определение: потенциальная энергия — это функция координат, являющаяся слагаемым в лагранжиане системы, и описывающая взаимодействие элементов системы. Единицей измерения энергии в СИ является Джоуль.
Потенциальная энергия 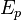 в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
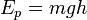
где 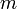 — масса тела,
— масса тела, 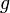 — ускорение свободного падения,
— ускорение свободного падения,  — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.
10. Си́ла упру́гости — сила, возникающая при деформации тела и противодействующая этой деформации.
В простейшем случае одномерных малых упругих деформаций формула для силы упругости имеет вид (Закон Гука):
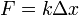 ,
,
где  — жёсткость тела,
— жёсткость тела,  — величина деформации.
— величина деформации.
В словесной формулировке закон Гука звучит следующим образом:
Сила упругости, возникающая при деформации тела, прямо пропорциональна удлинению тела и направлена противоположно направлению перемещения частиц тела относительно других частиц при деформации.
Потенциальная энергия растянутой пружины: 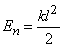
Такое же выражение получается для сжатой пружины.
11. Закон сохранения энергии в механических процессах:
Ek1 + Ep1 = Ek2 + Ep2
Величину E, равную сумме кинетической и потенциальной энергий системы, называют механической энергией системы:

Так как изменение полной энергии системы в рассматриваемом случае согласно уравнению (6.27) равно нулю, то энергия остается постоянной:

в рассматриваемом конкретном случае 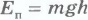 и
и 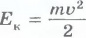 , можно закон сохранения механической энергии записать так:
, можно закон сохранения механической энергии записать так:

или

Для системы, состоящей из тела массой m и пружины, закон сохранения механической энергии имеет вид
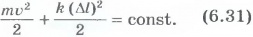
12. Абсолютно упругий удар — модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.
Для математического описания простейших абсолютно упругих ударов, используется закон сохранения энергии и закон сохранения импульса.
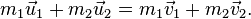
Здесь m1, m2 - массы первого и второго тел. u1, v1 - скорость первого тела до, и после взаимодействия. u2, v2 - скорость второго тела до, и после взаимодействия.

Важно - импульсы складываются векторно, а энергии скалярно.
Абсолю́тно неупру́гий удар — удар, в результате которого компоненты скоростей тел, нормальные площадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.
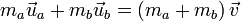
Где v это общая скорость тел, полученная после удара, ma - масса первого тела, ua - скорость первого тела до соударения. mb - масса второго тела, ub -скорость второго тела до соударения. Важно - импульсы являются величинами векторными, поэтому складываются только векторно.
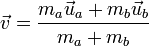
Как и при любом ударе, при этом выполняются закон сохранения импульса и закон сохранения момента импульса, но не выполняется закон сохранения механической энергии. Часть кинетической энергии соудареямых тел в результате неупругих деформаций переходит в тепловую.
Хорошая модель абсолютно неупругого удара — сталкивающиеся пластилиновые шарики.
13. Момент силы — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению), на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело.
момент силы частицы определяется как векторное произведение:
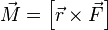
где 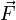 — сила, действующая на частицу, а
— сила, действующая на частицу, а  — радиус-вектор частицы.
— радиус-вектор частицы.
Момент инерции — скалярная (в общем случае — тензорная) физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
Различают несколько моментов инерции — в зависимости от многообразия, от которого отсчитывается расстояние точек.
Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина Ja, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси:
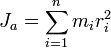 ,
,
где:
· mi — масса i -й точки,
· ri — расстояние от i -й точки до оси.
Осевой момент инерции тела Ja является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.
 ,
,
где:
·  — масса малого элемента объёма тела
— масса малого элемента объёма тела  ,
,
·  — плотность,
— плотность,
·  — расстояние от элемента
— расстояние от элемента  до оси a.
до оси a.
Если тело однородно, то есть его плотность всюду одинакова, то

14. момент инерции относительно любой оси равен

Момент инерции однородной прямоугольной пластинки, например с массой М, шириной ω и длиной L относительно оси, перпендикулярной к ней и проходящей через ее центр, равен просто
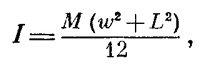 Момент инерции равен
Момент инерции равен

|
Общая формула для нахождения момента инерции объекта относительно оси z имеет вид

|
Теоре́ма Гю́йгенса — Ште́йнера, или просто теорема Штейнера (названа по имени швейцарского математика Якоба Штейнера и голландского математика, физика и астронома Христиана Гюйгенса): момент инерции  тела относительно произвольной оси равен сумме момента инерции этого тела
тела относительно произвольной оси равен сумме момента инерции этого тела  относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела
относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела 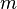 на квадрат расстояния
на квадрат расстояния  между осями:
между осями:
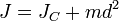
где
 — известный момент инерции относительно оси, проходящей через центр масс тела,
— известный момент инерции относительно оси, проходящей через центр масс тела,
 — искомый момент инерции относительно параллельной оси,
— искомый момент инерции относительно параллельной оси,
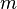 — масса тела,
— масса тела,
 — расстояние между указанными осями.
— расстояние между указанными осями.
15. Основное уравнение динамики вращательного движения имеет вид:
 (11), где β — тангенциальное ускорение.
(11), где β — тангенциальное ускорение.
16. Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел и остается постоянной, пока на систему не воздействуют внешние силы. В соответствии с этиммомент импульса замкнутой системы в любой системе координат не изменяется со временем.
Закон сохранения момента импульса есть проявление изотропности пространства относительно поворота.
В упрощённом виде: 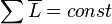 , если система находится в равновесии.
, если система находится в равновесии.

17. Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.
Основные кинематические характеристики вращательного движения тела — его угловая скорость (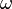 ) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:
) и угловое ускорение. Основные динамические характеристики вращательного движения — момент импульса относительно оси вращения z:

и кинетическая энергия

где Iz — момент инерции тела относительно оси вращения.
Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением

где ω1, ω2, и ω3 — главные компоненты угловой скорости.
В общем случае, энергия при вращении с угловой скоростью 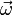 находится по формуле:
находится по формуле:
 , где
, где  — тензор инерции.
— тензор инерции.
При вращательном движении работа определяется проекцией момента сил на направление угловой скорости:
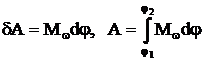 ,
,
если Мw = const, то А = Мw×j.
18. Гироско́п — устройство, способное реагировать на изменение углов ориентации тела, на котором оно установлено, относительно инерциальной системы отсчета. Простейший пример гироскопа — юла (волчок).
Упрощённо, поведение гироскопа описывается уравнением:

где векторы 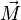 и
и  являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр
являются, соответственно, моментом силы, действующей на гироскоп, и его моментом импульса, скаляр  — его моментом инерции, векторы
— его моментом инерции, векторы 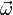 и
и  угловой скоростью и угловым ускорением.
угловой скоростью и угловым ускорением.
Отсюда следует, что момент силы 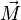 , приложенный перпендикулярно оси вращения гироскопа, то есть перпендикулярный
, приложенный перпендикулярно оси вращения гироскопа, то есть перпендикулярный  , приводит к движению, перпендикулярному как
, приводит к движению, перпендикулярному как 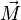 , так и
, так и , то есть к явлению прецессии. Угловая скорость прецессии
, то есть к явлению прецессии. Угловая скорость прецессии 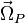 гироскопа определяется его моментом импульса и моментом приложенной силы[9]:
гироскопа определяется его моментом импульса и моментом приложенной силы[9]:

то есть 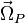 обратно пропорциональна скорости вращения гироскопа.
обратно пропорциональна скорости вращения гироскопа.
Гироскопический эффект лежит в основе конструкций разных приборов:
гирокомпаса, «искусственного горизонта» в самолетах, гироскопического
успокоителя качки корабля, гироскопического стабилизатора положения ракеты и
др. В ряде случаев при наличии в механизмах частей с быстрым вращением
гироскопические силы могут оказывать вредное влияние. Например, прирезком
повороте корабля быстровращающаяся ось турбины оказывает значительное
дополнительное давление на подшипники, что может привести к их разрушению.
Применяемые в технике гироскопы выполняют обычно в виде маховичка с утолщенным ободом, имеющего массу от нескольких граммов до десятков килограммов и закрепленного в кардановом подвесе. Чтобы сообщить гироскопу быстрое вращение, его делают ротором быстроходного электромотора постоянного или переменного тока. В авиации применяются гироскопы с ротором в виде воздушной турбинки, приводимой в движение струей воздуха. Иногда гироскопы выполняют в форме шара (шар-гироскоп) с подвесом на воздушной пленке, образуемой потоком сжатого воздуха; воздушные (газовые) опоры могут также применяться в осях подвеса ротора и кардановых колец.
19. Класси́ческая тео́рия тяготе́ния Ньюто́на (Зако́н всео́бщего тяготе́ния Ньюто́на) — закон, описывающий гравитационное взаимодействие в рамках классической механики. Этот закон был открыт Ньютоном в 1666 году. Он гласит, что сила гравитационного притяжения между двумя материальными точками массы  и
и  , разделёнными расстоянием
, разделёнными расстоянием  , пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:
, пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними — то есть:
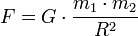
Здесь  — гравитационная постоянная, равная
— гравитационная постоянная, равная 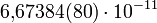 м³/(кг с²).
м³/(кг с²).
Потенциальная энергия 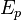 в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
в поле тяготения Земли вблизи поверхности приближённо выражается формулой:
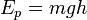
где 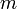 — масса тела,
— масса тела, 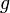 — ускорение свободного падения,
— ускорение свободного падения,  — высота положения центра масс тела над произвольно выбранным нулевым уровнем.
— высота положения центра масс тела над произвольно выбранным нулевым уровнем.
20. Напряжённость гравитацио́нного по́ля — векторная величина, характеризующая гравитационное поле в данной точке и численно равная отношению силы тяготения, действующей на тело, помещённое в данную точку поля, к гравитационной массе этого тела:

Гравитацио́нный потенциа́л — скалярная функция координат и времени, характеризующая гравитационное поле в классической механике. Имеет размерность квадрата скорости, обычно обозначается буквой 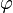 . Гравитационный потенциал равен отношению потенциальной энергии материальной точки, помещённой в рассматриваемую точку гравитационного поля, к массе этой точки.
. Гравитационный потенциал равен отношению потенциальной энергии материальной точки, помещённой в рассматриваемую точку гравитационного поля, к массе этой точки.
Движение частицы в гравитационном поле в классической механике определяется функцией Лагранжа, имеющей в инерциальной системе отсчета вид:
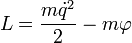 , где:
, где: 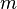 — масса частицы,
— масса частицы, 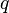 — координата частицы,
— координата частицы, 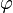 — потенциал гравитационного поля.
— потенциал гравитационного поля.
Подставляя выражение для лагранжиана L в уравнения Лагранжа:
 ,
,
получаем уравнения движения
 .
.
Гравитационный потенциал точечной частицы равен:  , где
, где  — гравитационная постоянная,
— гравитационная постоянная, 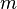 — масса частицы,
— масса частицы,  — расстояние от частицы.
— расстояние от частицы.
Потенциальная энергия частицы в гравитационном поле равна ее массе, умноженной на потенциал поля. Для потенциальной энергии любого распределения масс справедливо выражение:
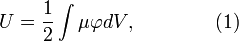
где  — плотность массы тела,
— плотность массы тела, 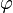 — гравитационный потенциал,
— гравитационный потенциал,  — объём тела.
— объём тела.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 448; Нарушение авторских прав?; Мы поможем в написании вашей работы!