Математическое выражение для кривой Лиссажу

Вынужденные колебания. Резонанс. Колебания, происходящие под действием внешней периодической силы, называются вынужденными колебаниями. Внешняя периодическая сила, называемая вынуждающей, сообщает колебательной системе дополнительную энергию, которая идет на восполнение энергетических потерь, происходящих из-за трения. Если вынуждающая сила изменяется во времени по закону синуса или коси­нуса, то вынужденные колебания будут гармоническими и незатухающими. В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из со­стояния равновесия), в случае вынужден­ных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на пре­одоление трения, и потому полная энергия колебательной системы no-прежнему ос­тается неизменной.

Частота вынужденных колебаний равна частоте вынуждающей силы. В случае, когда частота вынуждающей силы υ совпадает с собственной частотой колебательной системы υ₀, происходит рез­кое возрастание амплитуды вынужденных колебаний — резонанс. Резонанс возникает из-за того, что при υ = υ₀ внешняя сила, действуя в такт со свободными колебаниями, все время сонаправлена со скоростью колеблющегося тела и совершает по­ложительную работу: энергия колеблющегося те­ла увеличивается, и амплитуда его колебаний становится большой. График зависимости амплитуды вынужденных колебаний А_т от частоты вынужда­ющей силы υ представлен на рисунке, этот график называется резонансной кривой:

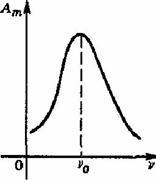
Явление резонанса играет большую роль в ря­де природных, научных и производственных процессов. Например, необходимо учитывать явление резонанса при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены.

30 вопрос

СЛОЖЕНИЕ ОДИНАКОВО НАПРАВЛЕННЫХ КОЛЕБАНИИ.

Рассмотрим сложение одинаково направленных колебаний одного периода, но отличающихся начальной фазой и амплитудой.Уравнения складываемых колебаний заданы:Х2 = А 2 • s in (сот -}- <рг), где х\, х2 — смещения; Ль А2 — амплитуды; фь фг — начальные фазы складываемых колебаний.2-4), на которой отложены векторы амплитуд AV и А2 складываемых колебаний под углами q>i и fj к оси ОХ иЕсли равномерно вращать систему векторов и проектировать векторы на ось OY, то их проекции будут совершать гармонические колебания в соответствии с заданными уравнениями.Отсюда следует вывод, что суммарное движение — гармоническое колебание, имеющее заданную циклическую частоту со.Найдем модуль амплитуды А результирующего колебания.Начальная фаза ср результирующего колебания определяется по тангенсу ее.10), видим, что при сложении одинаково направленных колебаний возможны следующие случаи.(можно считать, что q>i—ф2=0), то колебания однофазные и усиливают друг друга.результирующая суммарная амплитуда равна сумме амплитуд составляющих колебаний.2 = (2л + 1)«, колебания ослабляют друг друга и результирующая амплитуда равна разности амплитуд складываемых колебаний:колебания взаимно гасят друг друга.Если складываемые колебания имеют одинаковые амплитуды (А1=А2=А), но различные периоды, при этом периоды Т\ и Т2 отличаются незначительно друг от друга, т.разность периодов АТ = Т\—Т2 имеет небольшое значение, то при сложении таких колебаний наблюдаются биения.усиливают друг друга, и амплитуда суммарного колебания становится равной 2Л,-.При постепенном увеличении разности фаз в другие интервалы времени колебания становятся противофазными, и суммарная амплитуда обращается в нуль.Амплитуда сложного колебания при биениях изменяется со временем периодически.Число п биений в секунду (число повторений максимумов или минимумов в 1 сек) определяется разностью частот складываемых колебаний, т.Результирующая картина сложения колебаний при биенияхБиение можно наблюдать при звучании двух камертонов, если частоты их колебаний близки друг к другу.2-5 показана результирующая картина сложения колебаний при биениях.Таким образом, возвращающая сила пропорциональна смещению, и маятник при малых углах отклонения совершает гармонические колебания.Найдем выражение для периода колебаний математического маятника.Согласно этой формуле можно записать, что и тогда закон изменения периода колебаний запишется в виде r =: т.при постоянной длине маятника период его колебаний линейно зависит от расстояния до центра Земли.

Физическим маятником называется твердое тело, закрепленное на неподвижной горизонтальной оси (оси подвеса), не проходящей через центр тяжести, и совершающее колебания относительно этой оси под действием силы тяжести.При небольших углах отклонения а физический маятник также совершает гармонические колебания.С учетом этого выражения формулу периода колебаний физического маятника можно записать в видеУ mgL — приведенная длина маятника, /— момент инерции относительно оси О колебаний, m — масса маятника, L — расстояние между центром тяжести С маятника и осью колебания О.

31 вопрос

СЛОЖЕНИЕ ВЗАИМНО ПЕРПЕНДИКУЛЯРНЫХ КОЛЕБАНИЙ.

Остановимся на сложении колебаний материальной точки М, которая одновременно колеблется в двух взаимно перпендикулярных направлениях, например в направлении осей X и У (рис.Составляющие колебания имеют одинаковую частоту и фазу и различные амплитуды А\ и А2.Сложение взаимно перпендикулярных колебаний, имеющих одинаковые частоту и фазу = Al sin (от, = Л2 sin шт.Результирующее движение также является гармоническим колебанием, так как смещение, определяющее положение колеблющейся точки, согласно формулам (2.Фазы составляющих колебаний отличаются на я/2, а частоты равны.' Уравнения составляющих колебаний запишутся так:траекторией результирующего движения является эллипс с полуосями, равными амплитудам А\ и AZ 'Составляющих колебаний (рис.Сложение взаимно перпендикулярных колебаний, имеющих одинаковую частоту и разность фаз Л/2 a) S)В общих случаях сложения взаимно перпендикулярных колебаний колеблющаяся точка движется по кривым, называемым фигурами Лиссажу (рис.Конфигурация этих кривых зависит от соотношения амплитуд, начальных фаз и периодов составляющих колебаний.Для этого на горизонтальный вход осциллографа подают электрические колебания с частотой 50 гц, а на вертикальный вход — электрические колебания, частоту которых можно изменять.Изменяя эту частоту и тем самым соотношение частот составляющих колебаний, можно получить большой набор фигурПо-«этому можно сказать, что процесс распространения колебаний в данной среде есть волновойлфоцесс.Например, если закрепить один конец резинового жгута, а другой конец привести в колебание, то по длине жгута начнут распространяться колебания и возникнет волновое движение.Это графическое представление волнового процесса имеет совсем иной смысл, чем график смещения при гармоническом колебании, на котором изображалось смещение одной и той же точки в зависимости от времени (см.Точка / приводится в гармоническое колебание с периодом Т, направленное перпендикулярно линии /—5.Так как соседние точки связаны между собой упругими силами, они тоже приходят в колебание, но с некоторым запозданием.Колебание начали все точки, лежащие слева от точки 2.Прит=—Т точка / достигнет максимального отрицательносо смещения, точка 2 вернется в положение равновесия и колебания достигнут точки 4.Наконец, за время, равное периоду т=|Г, точка 1 вернется в положение равновесия, совершив полностью одно колебание.Колебания распространились до точки 5, все колеблющиеся точки образуют полную волну.При дальнейших колебаниях точек волновой процесс распространится вправо от точки 5.Помимо поперечных волн, в среде могут возникнуть продольные волны, в которых колебания частиц среды происходят вдоль •направления распространения волнового процесса,.В продольных волнах вследствие совпадения направлений колебаний частиц и волны появляются сгущения и разрежения.В твердых телах, где наряду с упругими деформациями растяжения и сжатия есть упругая деформация сдвига, могут одновременно происходить и продольные, и поперечные колебания, т.Периодом волны Т называется время одного полного колебания ее точек.

Волны со скоростью v распространяются от источника колебаний вдоль прямой.Уравнение колебаний точки В задано в таком виде х =Asin2itvT (242) где хв — смещение точки В, А — амплитуда ее колебаний, v — частота, т — время колебаний.Эти колебания дойдут до точки С через т', поэтому время колебаний точки С будет меньше t и составит (т —т').Смещение точки, которая участвует одновременно в двух колебаниях, равно алгебраической сумме х2 и х\:Каждая точка совершает гармоническое колебание с периодом Т.Физиологическое понятие — высота звука определяется частотой звуковых колебаний (физическая характеристика).С изменением частоты звуковых колебаний высота звука изменяется.В отличие от порога слышимости -порог болевого ощущения мало зависит от частоты колебаний.В том случае, когда имеется сложное 'периодическое движение, то его можно разложить на простые синусоидальные колебания.При этом частоты простых колебаний, например vb \z, vs и т., будут кратны частоте v основного колебания.Набор частот колебаний, присутствующих в данном звуке, называется его акустическим спектром.Процесс распространения звуковых волн в газах схематически можно представить следующим образом: источник механических колебаний передает эти колебания окружающим его газовым молекулам; в результате изменяется давление газа в данной микрообласти пространства.За время Т' приемник звука переместится на расстояние ±wT', а звук — на расстояние иТ', и тогда длина волны будет равна \ = иТ' ± wT' = (u ± о») Г', а частота звуковых колебаний, регистрируемых приемником, будет так какУльтразвуковые колебания могут быть получены с.Датчиком колебаний в акустических аппаратах обычно служит кварцевая пластина, заключенная между металлическими пластинами конденсатора, размеры которой определяют частоту ее собственных колебаний.При равенстве частоты электрических колебаний и одной из собственных частот колебаний пластины возникает резонанс, и кварцевая пластина становится источником сильных механических колебаний.Менее мощные ультразвуковые колебания с частотами порядка 700 тыс.В процессе колебаний атомов происходит переход потенциальной энергии в кинетическую и наоборот, т.Величина е = /zv называется к в а н т о м энергии при частоте колебаний v (h = = 6,62 • 10~34 дж • сек — постоянная Планка).Поэтому изменения энергии колебаний при невысоких температурах не наблюдаются.Возрастание температуры тела приводит к увеличению отклонений частиц при колебаниях от положений равновесия, что обусловливает тепловое расширение твердого тела.Внутренняя энергия твердого тела складывается из энергии колебаний его частиц.Колебания частиц для облегчения расчетов считаем гармоническими ') и независимыми друг от друга.Колебания атомов могут быть направлены по трем осям.Ч Силы, вызывающие колебания частиц в кристаллической решетке, не являются вазиупругими.В первом приближении можно считать, что они зависят от смещения х частиц по закону F = —kx+bx*, где член Ьх1 характеризует отклонение колебаний от гармонического характера.Под влиянием сил притяжения движение частиц превращается в тепловые колебания около узлов решетки.Пьезоэлектрические кристаллы широко применяются в качестве электромеханических преобразователей: стабилизаторов и фильтров радиотехнических частот, пьезоэлектрических манометров, излучателей и приемников ультразвуковых колебаний, пьезометров, звукоснимателей и т.Для работы в об- -ласти низких звуковых частот также применяются пластины, причем монтаж их ведется таким образом, чтобы они совершали колебания изгиба или кручения.Правило Матиссена утверждает, что зависимость удельногв электрического сопротивления от температуры р (Т) является ®* 259 сложной функцией, которая состоит из двух независимых слагаемых:, (8-38) где рост называется остаточным удельным сопротивлением, а рвд — идеальным удельным сопротивлением металла, которое соответствует сопротивлению абсолютно чистого металла и определяется лишь тепловыми колебаниями атомов.Если даже количество примесей и дефектов решетки свести к минимуму, то все-таки остается еще один фактор, влияющий на электрическое сопротивление металлов, — тепловое колебание атомов, которое, как утверждает квантовая механика, не прекращается и при тем'пературе(абсолютного нуля.В результате этих колебаний решетка перестает быть идеальной и в пространстве возникают переменные силы, действие которых приводит к рассеянию электронов, т.С точки зрения квантовой теории эти силь» появляются вследствие того, что электроны могут бмениваться фононами — квантами колебаний решетки.Электронные лампы используются в следующих целях: а) для преобразования переменного тока в постоянный (выпрямители); б) для усиления колебаний различных частот (усилители); в) для генерирования колебаний.Трехэлектродные лампы (триоды) широко применяются в радиоэлектронике и технике связи в качестве усилителей электрических сигналов и генераторов незатухающих колебаний.

Фигу́ры Лиссажу́ — замкнутые траектории, прочерчиваемые точкой, совершающей одновременно два гармонических колебания в двух взаимно перпендикулярных направлениях. Впервые изучены французским учёным Жюлем Антуаном Лиссажу. Вид фигур зависит от соотношения между периодами (частотами), фазами и амплитудами обоих колебаний. В простейшем случае равенства обоих периодов фигуры представляют собой эллипсы, которые при разности фаз 0 или 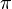вырождаются в отрезки прямых, а при разности фаз и равенстве амплитуд превращаются в окружность. Если периоды обоих колебаний неточно совпадают, то разность фаз всё время меняется, вследствие чего эллипс всё время деформируется. При существенно различных периодах фигуры Лиссажу не наблюдаются. Однако, если периоды относятся как целые числа, то через промежуток времени, равный наименьшему кратному обоих периодов, движущаяся точка снова возвращается в то же положение — получаются фигуры Лиссажу более сложной формы. Фигуры Лиссажу вписываются в прямоугольник, центр которого совпадает с началом координат, а стороны параллельны осям координат и расположены по обе стороны от них на расстояниях, равных амплитудам колебаний.

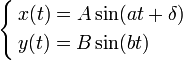
где A, B — амплитуды колебаний, a, b — частоты, δ — сдвиг фаз

Вид кривой сильно зависит от соотношения a / b. Когда соотношение равно 1, фигура Лиссажу имеет вид эллипса, при определённых условиях она имеет вид окружности (A = B, δ = π/2 радиан) и отрезка прямой (δ = 0). Ещё один пример фигуры Лиссажу — парабола (a / b = 2, δ = π/2). При других соотношениях фигуры Лиссажу представляют собой более сложные фигуры, которые являются замкнутыми при условии a / b — рациональное число.

Фигуры Лиссажу, где a = 1, b = N (N — натуральное число) и

Вопрос 32

Во́лны на пове́рхности жи́дкости — название разнообразных волн, возникающих на поверхности раздела между жидкостью и газом или жидкостью и жидкостью. Волны на поверхности жидкости различаются принципиальным механизмом колебания (капиллярный, гравитационный и т. д.), что приводит к различным законам дисперсии и, как следствие, к различному поведению этих волн.

ПРОДОЛЬНЫЕ И ПОПЕРЕЧНЫЕ ВОЛНЫ

В физике мы имеем дело с волнами различной природы: механическими, электромагнитными и т.д. Несмотря на отличия, эти волны имеют много общих черт. Волны, рассматриваемый параметр которых (смещение молекул, механическое напряжение, и т.д.) изменяется периодически вдоль оси распространения, называются продольными волнами. Если колебания происходят перпендикулярно оси распространения волны (как у электромагнитных волн, например), то такие волны называются поперечными.

Если взаимосвязь между частицами среды осуществляется силами упругости, возникающими вследствие деформации среды при передаче колебаний от одних частиц к другим, то волны называются упругими. К ним относятся звуковые, ультразвуковые, сейсмические и др. волны. На первой анимации изображён процесс распространения продольной упругой волны в решётке, состоящей из шариков, соединённых упругими пружинками. Каждый шарик колеблется по гармоническому закону в продольном направлении, совпадающем с направлением распространения волны. Амплитуда каждого шарика одинакова и равна A, а фаза колебаний линейно растёт с увеличением номера шарика на Dj т.е.

x ₀= A sin(w t); x ₁= A sin(w t+ Dj); x ₂= A sin(w t+ 2Dj); x ₃= A sin(w t+ 3Dj); и т.д.

где w -частота волны, t - время, Dj - изменение фазы от шарика к шарику

В поперечной волне колебания происходят в направлении, перпендикулярном направлению распространения волны. Как и в случае продольных волн амплитуды колебаний всех шариков одинаковы, а фаза линейно изменяется от шарика к шарику

y ₀= B sin(w t); y ₁= B sin(w t+ Dj); y ₂= B sin(w t+ 2Dj); y ₃= B sin(w t+ 3Dj); и т.д.

В общем виде уравнение распространения волны может быть записано в виде: z = A cos(w t - kx), где z - координата, по которой происходит движение частиц, x - координата оси, вдоль которой распространяется волна, k - волновое число, равноеw / v, v - скорость распространения волны. Зная частоту волны и скорость её распространения, мы можем найти сдвиг фаз между соседними шариками (частицами): Dj = (w / v)a, где a - расстояние между шариками в решётке.

На следующей анимации изображено наложение продольной и поперечной волн равной амплитуды, сдвинутых по фазе на 90 градусов. В результате каждая масса совершает круговые движения. Уравнение движения каждого шарика может быть описано уравнением:

x = A cos(w t+ j₀); y = A sin(w t+ j₀)

У волн, наблюдаемых на поверхности жидкости, так называемых поверхностных волн, взаимосвязь между соседними элементами поверхности жидкости при передаче колебаний осуществляется не силами упругости, а силами поверхностного натяжения и тяжести. Колебания масс в сетке моделируют движение молекул в волне на поверхности жидкости. В случае малой амплитуды волны каждая масса движется по окружности, радиус которой убывает с расстоянием от поверхности. Массы внизу сетки находятся в покое.

Волны на поверхности жидкости не являются ни продольными, ни поперечными. Как мы можем видеть на анимации, красный шарик, моделирующий молекулу поверхности жидкости, движется по круговой траектории. Таким образом, волна на поверхности жидкости представляет собой суперпозицию продольного и поперечного движения молекул.

каждая волна распространяется с какой-то скоростью. Под скоростью волны понимают скорость распространения возмущения. Например, удар по торцу стального стержня вызывает в нем местное сжатие, которое затем распространяется вдоль стержня со скоростью около 5 км/с.

Скорость волны определяется свойствами среды, в которой эта волна распространяется. При переходе волны из одной среды в другую ее скорость изменяется.

Поскольку скорость волны - величина постоянная (для данной среды), то пройденное волной расстояние равно произведению скорости на время ее распространения. Таким образом, чтобы найти длину волны, надо скорость волны умножить на период колебаний в ней:

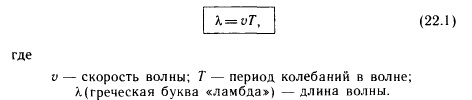
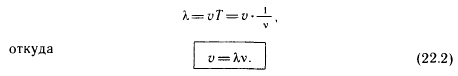
33 вопрос

Таким обpазом, уpавнение плоской волны без диспеpсии имеет следующий вид:

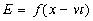или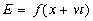

(1.2)

Здесь v есть фазовая скоpость волны, а вид функции f может быть любым. Наиболее интеpесными являются пеpиодические синусоидальные волны, когда функция f пpедставляет собой синус или косинус аpгумента (синус и косинус отличаются дpуг от дpуга только сдвигом по фазе на 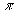/2). В качестве аpгумента синуса не м ожет быть пpосто (x-vt), т.к. эта величина pазмеpная, тогда как аpгумент синуса должен быть безpазмеpным. Поэтому синусоидальная волна описывается следующим уpавнением:

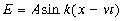
Всякая функция, удовлетворяющая уравнению (5.6.4), описывает некоторую волну, причем корень квадратный из величины, обратной коэффициенту при производной по времени, есть фазовая скорость волны.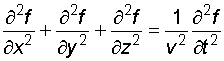

Используя оператор Лапласа, волновое уравнение можно записать в виде ,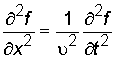

34 вопрос

ЕТА ВОЛНЫ
Бета-волны – это быстрые волны, низкой амплитудой, приблизительно от 14 до 40 циклов в секунду (Hz). Бета-волны генерируются естественным путем, когда мы находимся в состоянии бодрствования, тревожном состоянии сознания. Изначально бета-волны представляют собой процесс обработки данных, включающий сотни мелких вычислений между двумя ближайшими областями коры, которые работают вместе для достижения результата ("Что это был за звук или образ?", "Сколько будет 2 + 3?", "Это опасно?", "Я боюсь», «Что мне делать?").Существуют 3 основные подгруппы бета-волн: Гамма (от 35 до 40 Hz), Бета 2 (от 24 до 34 Hz) и Бета 1 (от 14 до 23). Гамма волны, самые быстрые, отражают пиковую деятельность сознания. Чрезмерная активность бета 2 связана с повышенными эмоциональными состояниями, такими как волнение и страх. Частоты бета 1 связаны с познавательными процессами, такими как решение проблем и мышление.

АЛЬФА ВОЛНЫАльфа волны вибрируют в диапазоне примерно от 8 до 13 Hz. Альфа активность представляет собой вибрации между фрагментами коры и зрительным бугром, известным как корково-таламическая петля.Альфа волны проявляются в период сенсорного покоя (например, в тихой комнате с закрытыми глазами), умственной релаксации, глубокой релаксации, медитации или умиротворенного сознания (диссоциации). Альфа волны – вожделенный результат медитирующих. Традиционные методы медитации требуют 10 лет практики, чтобы достичь производства идеальных альфа волн. Производство альфа волн сокращается в момент обработки данной частью мозга сенсорной информации, а также в процессе решения проблем и познавательной активности. Увеличение количества альфа волн дает:чувство умиротворения улучшенное академическую успеваемостьт епло в конечностях повышенную производительность на рабочем месте ощущение благополучия снижение тревожности, улучшение сна

ТЕТА ВОЛНЫ
Частоты тета волн - от 4 до 8 Hz. Тета волны ассоциируются с состоянием сна, «сумеречным» состояние, состоянием гипнотического транса, БДГ – фазой сна и состоянием сновидений. В этом состоянии увеличивается активность памяти. Память улучшается (особенно долговременная память), повышается доступ к подсознанию, возможность свободных ассоциаций, повышается креативность, имеют место неожиданные озарения. Это таинственное, особое состояние сознания. Долгое время ученые не могли исследовать это состояние мозга, т.к. обычный человек не может долгое время в нем оставаться без того, чтобы ни свалиться в сон (что также дает большое количество тета волн).ДЕЛЬТА ВОЛНЫДельта волны – самые медленные волны мозговой активности с частотой, колеблющейся от 1 до 4 Hz. Дельта волны доминируют, когда мы засыпаем и продолжают преобладать в состоянии глубокого сна.Повышенная активность дельта волн наблюдается также как следствие мозговых травм, когда сформировалась ткань рубца (обратная связь корково-таламической петли нарушается). Возрастает очевидность того факта, что некоторые люди могут оставаться в неком подобии сознания на фоне активности дельта волн.

Дата добавления: 2014-01-04