Метод Жордана-Гаусса

Метод Жордана-Гаусса або метод повного виключення полягає в одночасному виключенні якоїсь із змінних з усіх рівнянь, крім одного.

Алгоритм:

1-крок. Вибираємо ведучий елемент (перестановкою рівнянь можна добитися того, що 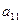буде найбільшим за модулем коефіцієнтом при 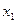). Поділимо перше рівняння системи на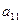

		(**)
			…
		…
…	…	…	…	…
		…
			…
		…
…	…	…	…	…
		…
…	…	…	…	…	…	…
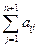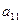
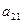
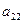
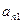
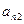
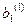
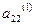
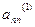
n			…
		…
…	…	…	…	…
		…

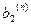
В усіх інших рівняннях виключаємо 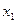, тобто система зводиться до I-кроку,

де ; (*),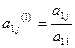

останній стовпчик обчислюється двічі: 1 раз - за формулою (*);

2-ий - раз за формулою (**)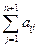

Якщо обчислення виконані правильно, то (*) = (**).

Результат записується з останнього 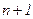-го кроку.

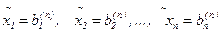
Позначимо вектор стовпчик наближеного розв’язку через .
Назвемо нев’язкою різницю між наближеним значенням розв’язку та точним:

=

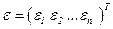Тоді наближений розв’язок 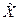можемо записати як 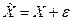. Підставив його у задану систему, отримаємо нову систему з n лінійних неоднорідних рівнянь

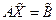, або 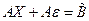. Зважаючи на те, що , матимемо

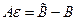- рівняння, з якого можемо знайти.

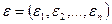Воно відрізняється від щойно нами розв’язаноготільки стовпчиком вільних членів. То для його розв’язування можна скористатися тими же таблицями, що і для знаходження Х, тільки обчислювати заново останні два стовпчики

Застосування метода Жордана-Гаусса, якщо тільки ведучі елементи за модулем є істотно більші за інші, забезпечує малі нев'язки якщо задача добре обумовлена, то розв’язок буде стійким.

Дата добавления: 2014-01-04