Одномерные колебания однородной струны

Колебания цепочки атомов 2-х сортов

Колебания цепочки одинаковых атомов

Одномерные колебания однородной струны

Основы динамики кристаллической решетки

Лекция 7

7.4 Фононы

До сих пор мы считали, что частицы находящиеся в узлах кристаллической решетки, являются неподвижными. Это предположение позволило нам разобраться с геометрией кристаллов и разобраться с природой сил взаимодействия частиц решетки. В то же время ряд физических свойств, в частности теплоемкость, теплопроводность, термическое расширение, электропроводность и др., не может быть объяснен без учета колебания частиц в узлах кристаллической решетки. В твердом теле атомы при любой температуре непрерывно совершают колебания около их среднего положения равновесия. При небольших амплитудах такие колебания можно считать гармоническими. С повышением температуры амплитуды и энергии этих колебаний увеличиваются. Так как атомы в твердом теле сильно связаны друг с другом, то возбуждение колебаний одного из атомов передается ближайшим атомам, которые, в свою очередь, передают это возбуж­дение своим соседям и т. д. Все возможные колебания сильно связанных между собой атомов можно представить как совокупность взаимодействующих упругих волн различной длины, распространяющихся по всему объему кристалла. Рассмотрим ряд простейших моделей, учитывающих динамику колебаний и найдем закономерности колебаний частиц в узлах решетки.

Рассмотрим распространение продольных волн в однородной неограниченной струне с линейной плотностью r. В этом случае движение каждого из элементов струны происходит лишь в направлении ее длины. При распространении продольной волны на элемент толщиной Dx (см. рисунок 7.1) действуют силы: слева Ss(x) и справа Ss(x+Dx), где S - площадь поперечного сечения струны, s(x) и s(x+Dx) - нормальные упругие напряжения.

На элемент Dx действует результирующая сила

F= Ss(x+Dx) - Ss(x).

Под действием этой силы элемент Dx испытывает смещение.

Обозначив u(x,t) смещение центра масс элемента Dx, запишем в соответствии со вторым законом Ньютона уравнение его движения

rSDx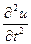= Ss(x+Dx) - Ss(x),

здесь rSDx=m - масса элемента Dx, а 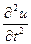- ускорение. Уравнение можно переписать в виде

r =.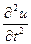

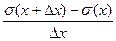При Dx®0 оно перейдет в уравнение

r =.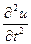

Согласно закону Гука для изотропных твердых тел

s=Еe,

где Е - модуль упругости (модуль Юнга), - деформация в точке.

Отсюда

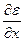= Е = Е .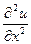

Тогда уравнение движения для смещения u(x,t) окончательно примет вид

=.

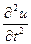Это обычное волновое уравнение для упругих волн, распространяющихся вдоль струны. Решение этого уравнения будем искать в виде бегущей монохроматической волны:

u=u₀exp[i(kx-wt)]= u₀ sin 2p (x/l-νt)= u₀sin(kx-wt)

где u₀ - амплитуда колебания, ν - частота колебаний, w = 2pν - круговая частота, t - время, l - длина волны, k = 2p/l - волновое число.

После подстановки последнего выражения в волновое уравнение получим дисперсионное соотношение

.

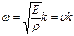Из дисперсионного соотношения следует, что для упругой волны, распространяющейся в неограниченно протяженной струне, частота колебаний линейно зависит от волнового числа (см. рисунок 7.2).

При этом скорость распространения волны для данного материала - величина постоянная. Для железной струны (E=2,1×10¹¹ Па, r=7,8×10³ кг/м³) имеем =5×10³ м/с.

Как видно из рисунка 7.2, модуль волнового числа может меняться от 0 до ¥, а следовательно, частота колебаний меняется непрерывно от 0 до ¥. Поскольку энергия Е=2πhω, то энергия колебаний может неограниченно возрастать. Это противоречит физическим представлениям о строении кристаллической решетки. Следовательно, модель струны является слишком грубой вследствие предположения о непрерывности распределения вещества в объеме кристалла. Поэтому рассмотрим случай дискретного распределения вещества.

Дата добавления: 2014-01-04