Механизмы теплопроводности твердых тел

В основе механизма передачи теплоты за счет теплопроводности лежит представление о переносе энергии частицами газа.

В диэлектриках процесс передачи теплоты происходит в результате взаимодействия фононов, подчиняющихся законам фононного газа. В основе механизма, описывающего перенос теплоты в любом газе, лежит кинетическая формула Дебая:

,

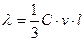где - коэффициент теплопроводности; С - удельная теплоемкость; v - средняя скорость фононов, приблизительно равная скорости звука в кристаллах; l - средняя длина свободного пробега фононов.

Проанализируем на основании кинетической формулы Дебая зависимость коэффициента решеточной теплопроводности от температуры.

Можно считать, что v слабо зависит от температуры, поэтому С и l являются величинами, определяющими зависимость фононной теплопроводности от температуры. При высоких температурах теплоемкость приближается к предельному значению, определяемому законом Дюлонга и Пти, т. е. перестает зависеть от температуры. Поэтому зависимость теплопроводности от температуры будет определяться температурными изменениями длины свободного пробега фононов. А так как число фононов возрастает с увеличением температуры, то следует ожидать, что длина свободного пробега фононов будет изменяться обратно пропорционально температуре. Тогда при высоких температурах .

При понижении температуры среднее число фононов спадает по экспоненте, а это означает, что длина свободного пробега фонона будет экспоненциально увеличиваться с понижением температуры:

,

где 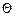- температура Дебая.

С другой стороны, теплоемкость с понижением температуры будет уменьшаться в соответствии с законом Дебая как Т³, при этом в целом теплопроводность будет увеличиваться за счет резко возрастающего экспоненциального члена для длины свободного пробега фононов (правый участок кривой на рисунке 8.3).

При приближении к абсолютному нулю длина свободного пробега становится сравнимой с размерами образца и перестает зависеть от температуры. В результате этого, при дальнейшем понижении температуры коэффициент теплопроводности вплоть до нуля будет резко спадать, так же, как и теплоемкость т.е. как Т³ (левый участок кривой на рисунке 8.3).

Описанная выше зависимость решеточной теплопроводности от температуры хорошо подтверждается экспериментальными данными.

Передачу теплоты в металлах можно рассматривать на основе представления о наличии в них электронного газа (электронов в зоне проводимости). В соответствии с этим представлением из формулы Дебая следует закон Видемана -Франца - Лоренца:

,

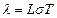где σ - удельная электропроводность, L - число Лоренца.

Универсальность этой записи заключается в том, что все неучтенные особенности поведения электрона в твердом теле можно выразить различным значением числа Лоренца. Нетрудно видеть, что, зная значение электропроводности материала и его температуру, можно рассчитать и его теплопроводность. Экспериментальные исследования позволили установить справедливость закона Видемана -Франца - Лоренца для всех металлов.

Таким образом, изменяя число Лоренца в зависимости от состояния электронного газа, т. е. от взаимодействия электронов друг с другом, с решеткой или с дефектами, можно подобрать его значение для любого металла так, что формула Видемана - Франца - Лоренца будет удовлетворительно описывать и объяснять механизм теплопроводности.

Принято считать, что в полупроводниках имеет место перенос теплоты и электронами, и фононами, а при высоких температурах возможно еще наличие добавочной теплопроводности, вызванной фотонами, экситонами и пр. Считают, что при этом теплопроводность подчиняется закону аддитивности, т. е. 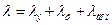, и исходя из этого проводят анализ механизма теплопроводности в полупроводниках и рассчитывают ее значение. При этом точное определение числа Лоренца еще более усложняется из-за большего разнообразия электронных состояний в полупроводниках по сравнению с таковыми в металлах, а трудности в определении фононной теплопроводности по существу остаются теми же, что и в диэлектриках.

Дата добавления: 2014-01-04