Правила Кирхгофа

В практике возникает необходимость расчета токов сопротивления, Э. Д. С. для разветвленных электрических цепей. Эта задача упрощается, если пользоваться правилам Кирхгофа. Рассмотрим изображенную на Рис.59 произвольную электрическую цепь.

Рисунок 59

Назовем узлами все точки в которых сходятся не менее трех проводников (узлы А, В, С, D). В цепи постоянного тока потенциалы всех точек цепи и узлов остаются неизменными. Т. е. в узлах не могут накапливаться электрические заряды ни положительного, ни отрицательного знака. В противном случае произошло бы изменение потенциалов узлов и текущих в цепи токов. Т. о. за единицу времени, одинаковое количество электричества входит в узел, и выходит из него. Будем соблюдать правило знаков: ток, текущий из узлов, считается положительным, текущий от узла - отрицательным. Напишем уравнение для узла А (см. рис. 5)

Аналогичные уравнения можно написать для узлов В, С, которые независимы друг для друга. Для узла В,для С .

Мы получим систему уравнений, выражающих первое правило Кирхгофа.

- Алгебраическая сумма токов, сходящихся в узле равна 0. Составим уравнение для узла D: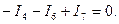

Видно, что данные токи уже входили в предыдущие три уравнения, поэтому это уравнение не является независимым. Поэтому число независимых уравнений меньше числа узлов, а следовательно, и числа неизвестных токов. Т. о. чтобы определить все неизвестные величины необходимо составить дополнительные уравнения. Для этой цели служит второе правило Кирхгофа.

Рассмотрим замкнутый контур, например, . Обозначим потенциалы узлов А и В -, соответственно . Будем условно считать за положительное направление обхода по часовой стрелке (см. рис. 5). Как видно из рисунка ток положительный и - положительный. Падение напряжения на участке АВ: .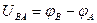

R₃- полное сопротивление участка и внутреннего сопротивления источника тока. И согласно закону Ома имеем:

Для второй ветви ток отрицательны и

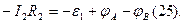
Складывая равенства (24) и (25), получим

второе правило Кирхгофа для замкнутого контура

«Алгебраическая сумма произведений токов на сопротивления в ветвях замкнутого контура равна алгебраической сумме Э. Д. С., встречающихся в этом контуре».

Вопросы для самоконтроля

1. Что называется силой и плотностью тока? Их единицы измерения?

2. Назовите условия возникновения и существования электрического тока.

3. Что такое сторонние силы? Какова их природа?

4. В чем заключается физический смысл электродвижущей силы, действующей в цепи? Напряжения? Разности потенциалов?

5. Какова связь между сопротивлением и проводимостью, удельным сопротивлением и удельной проводимостью?

6. выведите законы Ома и Джоуля - Ленца в дифференциальной форме

7. Как формулируются правила Кирхгофа? На чем они основаны?

СПИСОК ЛИТЕРАТУРЫ

Дата добавления: 2014-01-04