Демультплексори

End.

Until

Begin

Repeat

Begin

Vаr

Begin

Var

End.

Begin

Begin

Vаr

Магнітним полем називають вид матерії, за допомогою якої здійснюється силова дія на движущие-ся електричні заряди, поміщені в поле, і інші тіла, що володіють магнітним моментом. Магнітне поле є одна з форм прояву електромагнітного поля.

Х 290

Х 20

Х 420 х 0,75

Х 0,5

Аналогічно розраховується потужність кухні з випуску інших видів страв. Зокрема, для визначення потужності кухні (цеху) з випуску других страв враховується площа жарових поверхонь плит, електрошаф, місткість електро-сковорід, фритюрниць та іншої апаратури, тривалість про­цесів смаження, тушкування, а також час на організаційно-технологічні та інші простої.

Підвищення коефіцієнта використання потужності кух­ні має важливе значення для збільшення випуску і реалі­зації продукції, покращання всіх економічних показників підприємства.

На виробничу потужність підприємства громадського харчування безпосередньо впливають:

• основні фонди, тобто споруди;

• обладнання і рівень ефективності їх використання;

• асортимент і особливості видів продукції власного виробництва,

• якість сировини і продуктів;

• застосування прогресивних технологій і апаратури;

• наявність інструментів, інвентарю, пристосувань, внутрішньоцехових транспортних засобів тощо.

На збільшення виробничої потужності підприємства суттєво впливають також спеціалізації працівників, їхній культурно-технічний рівень, рівень організації виробництва тощо.

Необхідними резервами підвищення виробничої по­тужності підприємства є:

• запровадження досягнень науково-технічного про­гресу, передового досвіду, прогресивних техноло­гій виробництва;

• концентрація і розподіл виробничих процесів;

• збільшення коефіцієнта використання наявного об­ладнання, технічного рівня і кваліфікації праців­ників виробництва;

• скорочення витрат часу на одиницю продукції, що випускається, тощо.

Одним із основних чинників, що визначають збільшен­ня виробничої потужності, є підвищення продуктивності праці, яке залежить при інших рівних умовах від рівня концентрації виробництва, спеціалізації підприємств гро­мадського харчування.

Пропускна спроможність обідньої зали — це макси­мально можлива кількість споживачів, яку зможе обслу­жити підприємство за одиницю часу (день, місяць тощо). Вона залежить від площі обідньої зали, середньої трива­лості приймання їжі одним споживачем, норми площі на одне місце, режиму роботи і використання поточних ліній комплектації і роздачі їжі.

Норми площі на одне місце диференційовані за типами підприємств залежно від методів обслуговування спожи­вачів, габаритів меблів та інших чинників.

Виходячи із середніх витрат часу на обслуговування одного споживача, розробляються нормативи оборотності місць за типами підприємств. У зв'язку з нерівномірністю завантаження обідньої зали протягом робочого дня фак­тична оборотність звичайно нижча за максимально можли­ву. Тому при плануванні слід враховувати дані про інтен­сивність потоку відвідувачів протягом дня.

Пропускна спроможність обідньої зали може бути визначена за такою формулою:

Пз х Ч х К

Пс = -------------------

Н х t

де Пс – пропускна спроможність зали для відвідувачів за день;

Пз – корисна площа зали, м²;

Ч – час роботи зали за день, хв;

К – коефіцієнт заповнення зали із врахуванням інтенсивності потоку відвідувачів протягом дня;

Н – норма площі на одне місце, м²;

t – тривалість приймання їжі одним споживачем, хв.

Приклад. Їдальня працює 7 год на день, із них 3,5 год — з половинним навантаженням (коефіцієнт заповнення — 0,75). Корисна площа зали для розміщення столів (без площі, що зайнята під вузлом розрахунку, буфетом, лінією роздачі їжі) — 183 м², типова норма площі на одне місце — 1,2 м², середня тривалість приймання їжі одним спожи­вачем — 20 хв.

У нашому прикладі

Пс = ------------------------- = 1089 (відвідувачів за день)

Якщо враховувати, що в нашому прикладі їдальня пра­цювала 290 днів за рік і обслужила 289,2 тис. відвідувачів, то коефіцієнт використання пропускної спроможності ста­новитиме

289,2 тис. осіб

------------------------ = 0,92.

Для характеристики використання пропускної спро­можності застосовується і такий показник, як коефіцієнт оборотності місць, що являє собою відношення кількості відвідувачів, які обслуговуються за день, до кількості місць в обідній залі.

Пропускну спроможність підприємства, що проекту­ється, визначають виходячи з кількості місць, що перед­бачається, і нормативу оборотності одного місця. При цьо­му необхідно враховувати, що середній час обслуговування одного споживача становить на підприємствах, що пра­цюють за принципом самообслуговування, приблизно 20— 30 хв, а в буфетах і закусочних — 15—20 хв. Пропускна спроможність підприємства за день обчислюється як добу­ток від множення кількості місць на оборотність одного місця.

Шляхами підвищення ефективності використання зали є раціональний режим і ритмічна робота підприємства. Необхідно вивчати й аналізувати інтенсивність потоку споживачів протягом дня, покращувати організацію праці і розстановку працівників.

У збільшенні пропускної спроможності обідніх залів важлива роль належить запровадженню прогресивних по­точних ліній комплектації і реалізації обідів, переведенню підприємств на самообслуговування з наступним розрахун­ком, збільшенню відпуску обідів за абонементами, більш раціональному розміщенню столів тощо. Цьому сприяє та­кож створення кооперативів громадського харчування, ор­ганізація роботи підприємств на умовах приватної влас­ності, бригадного та орендного підрядів.

Отже, розрахунки виробничої потужності і пропускної спроможності дають можливість активно впливати на робо­ту підприємств громадського харчування шляхом розробки реальних програм виробничо-торговельної діяльності, під­вищення ефективності використання матеріальних і тру­дових ресурсів.

Важлива роль у підвищенні ефективності використання всієї матеріально-технічної бази галузі відводиться удос­коналенню планування і розміщенню мережі підприємств громадського харчування.

Правильний вибір типу підприємства і його терито­ріальне розміщення впливають на зростання обсягів това­рообороту і випуску продукції, а отже, і на отримання най­більшого ефекту від експлуатації основних фондів.

3. Методика планування товарообороту та випуску продукції.

Характеристика методів планування товарообороту підприємств ресторанного господарства

Варіант плану товарообороту	Можливий метод планування	Сутність методу плануванні
Необхідний обсяг товарообороту	Програмно-цільовий метод або метод пря­мого розрахунку	Виходячи з цільового (необхідного) обсягу отримання прибутку, рівнів дохідності витратності діяльності, що склалися
Можливий обсяг товарообороту	Економіко-статистичний метод; метод середнього темпу рос­ту; метод змінної середньої; трендовий метод; факторно-ана­літичний метод	На основі вивчення динаміки товарообороту та перенесення основних закономірностей роз­витку на плановий період з урахуванням чинників, що впливають на обсяг товарообо­роту
	Метод еластичності щодо зміни купівель­них фондів населення району діяльності під­приємства	Виходячи з коефіцієнта елас­тичності між темпами зміни обсягу товарообороту та змі­ною купівельних фондів на­селення та прогнозу зміни ку­півельної спроможності спо­живачів підприємства
Ресурсозабезпечений обсяг товарообороту	Балансовий метод	Виходячи з можливих обсягів закупівлі товарів та іммобіліза­ції товарних залишків
	Трудовий метод	Виходячи із забезпеченості підприємства персоналом та трудомісткості товарообороту
	Нормативний метод	На базі використання збалан­сованих раціонів харчування для різних соціально-вікових і професійних груп населення, нормативів на одне місце для основних типів підприємств ресторанного господарства

ст. 62 – 23

Використання як основоположних тих чи інших даних залежить від типу підприємства та умов його роботи. Випуск страв на підприємстві ресторанного господарства можна розраховувати на основі планового меню страв, що потрібно виготовити протягом певного відрізку часу (тижня, декади, місяця). При складанні планового меню передбачають чергування асортименту страв і виготовлення поживної, смачної та різноманітної їжі.

Планування випуску обідньої та іншої продукції може бути здійснене на основі розрахунків виробничої потужності кухні й пропускної спроможності обідньої зали підприємства ресторанного господарства.

§ 12.1. ІНДУКЦІЯ МАГНІТНОГО ПОЛЯ

Аналогічно електростатичному полю, необхідно для магнітного поля ввести кількісну характеристику. Для цього вибирають деякий об'єкт – «пробне тіло», що реагує на магнітне поле. Як таке тіло досить узяти малу рамку із струмом, щоб можна було вважати, що рамка поміщається в деяку точку поля. Досвід показує, що на пробну рамку із струмом в магнітному полі діє момент сили М, залежний від ряду чинників, у тому числі і від орієнтації рамки. Максимальне значення М_mах залежить від магнітного поля, в якому знаходиться контур, і від самого контура: сили струму І, що протікає по ньому, і площі S, що охоплюється контуром, тобто

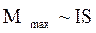. (12.1.1)

Величину

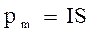• (12.1.2)

називають магнітним моментом контура із струмом. Таким чином

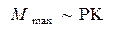(12.1.3)

Магнітний момент - векторна величина. Для плоского контура із струмом вектор рт направлений перпендикулярно площини контура і пов'язаний з напрямом струму I правилом правого гвинта (мал. 12.1).

Рис.12.1 Рис.12.2  

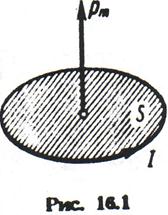
Магнітний момент є характеристикою не тільки контура струмом, але і багатьох елементарних частинок (протони, нейтрони, електрони і так далі), визначаючи поведінку їх в магнітному полі.

Одиницею магнітного моменту служить ампер-квадратный метр (А-м² ). Магнітний момент елементарних частинок, ядер, атомів і молекул виражають в особливих одиницях, званих або атомним ( µ_Б ), або ядерним ( µ_Я ), магнетоном Бору:

.

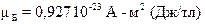
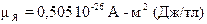Магнітна індукція в деякій точці поля рівна відношенню максимального такою, що обертає моменту, що діє на рамку із струмом в однорідному магнітному полі, до магнітного моменту цієї рамки:

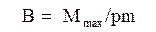(12.1.4 )

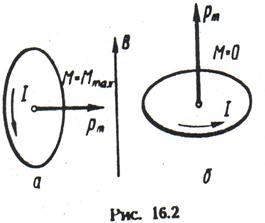
Вектор В співпадає по напряму з вектором pm в положенні стійкої рівноваги контура. На мал. 12.2 показано положення рамки із струмом в магнітному полі індукції В, відповідне максимальному моменту сили (а) і нульовому (б). Останній випадок відповідає стійкій рівновазі (вектори В і pm коллинеарны).

Одиницею магнітної індукції є тесла (Тл):

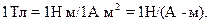
Таким чином, в полі з магнітною індукцією 1Тл на контур, магнітний момент якого 1А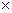м2, діє максимальний момент сили 1Н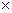м.

Магнітне поле графічно зображають за допомогою ліній магнітної індукції, дотичні до яких показують напрям вектора В. Густота ліній, тобто число ліній, що проходять через

Рис.12.3 Рис.12.4

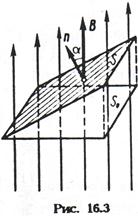
одиничну, перпендикулярно ним розташований майданчик, рівна модулю вектора В. Лінії магнітної індукції не мають початку або кінця і є замкнутими. Подібні поля називають вихровими. Циркуляція вектора магнітної індукції по будь-якій лінії магнітної індукції не рівна нулю:

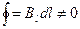(12.1.5)

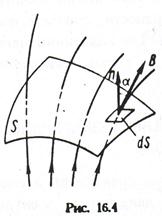
Розглянемо деякий майданчик S, що знаходиться в області однорідного магнітного поля індукції В (мал. 12.3). Проведемо лінії магнітної індукції через цей майданчик. Її проекція на площину, перпендикулярну лініям, рівна S₀ Число ліній, пронизливих S і S₀, однаково. Оскільки густина ліній відповідає значенню В, то загальне число ліній, пронизливих майданчики, рівне

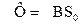. (12.1.6)

На ал.. 12.3 видно, що 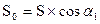звідки

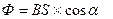або 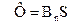, (12.1.7)

де 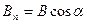- проекція вектора В на напрям нормалі n до майданчика;

Ф - магнітний потік.

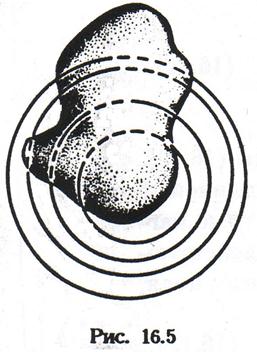
У більш загальному випадку, наприклад неоднорідне магнітне поле, поверхня, а не плоский майданчик (мал. 12.4), магнітний потік Ф також рівний числу ліній магнітної індукції, пронизливих поверхню.

Одиницею індукції магнітного поля, згідно (12.6), є вебер (Вб):

.

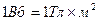З формули (12.7) видно, що потік може бути як позитивним (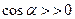), так і негативним

().

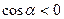Відповідно до цього лінії магнітної індукції, що виходять із замкнутої поверхні, вважають позитивними, а вхідні -отрицательными. Оскільки лінії магнітної індукції замкнуті, то магнітний потік крізь замкнуту поверхню рівний нулю (мал. 12.5).

§ 12.2. ЗАКОН АМПЕРА. ЕНЕРГІЯ КОНТУРА Із СТРУМОМ В МАГНІТНОМУ ПОЛІ

Одним з головних проявів магнітного поля є його силова дія на рухомі електричні заряди і струми. В результаті узагальнення численних досвідчених даних А.М. Ампером був встановлений закон, що визначає це силова дія.

Приведемо його до диференціальної форми, що дозволить обчислювати силу, що діє на різні контури із струмом, розташовані в магнітному полі.

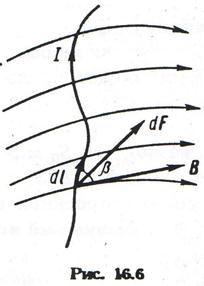
У провіднику, що знаходиться в магнітному полі, виділимо достатньо малу ділянку dl, який можна розглядати як вектор, направлений у бік струму (мал. 12.6). Твір Idl називають елементом струму. Сила, що діє з боку магнітного поля на елементом струму

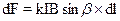• (12.1.8)

де k- коефіцієнт пропорційності; у

СІ k=1, тому

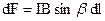(12.1.9)

або у векторній формі

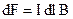• . (12.1.10)

Інтегруючи це рівняння, знаходимо силу, що діє на ділянку / провідника з боку магнітного поля:

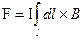(12.1.11)

	Рис. 12.6

Співвідношення (12.8) - (12.10) виражають закон Ампера.

Розглянемо деякі приклади на застосування формули (12.10).

1. Прямолінійна ділянка провідника із струмом I довжиною l, розташований в однорідному магнітному полі під кутом β до магнітної індукції В (рис 12.7). Для знаходження сили, що діє на цю частину провідника з боку магнітного поля, інтегруємо (12.11) і отримуємо

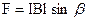• (12.1.12)

Рис.12.7 Рис.12.8  

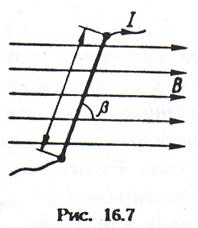
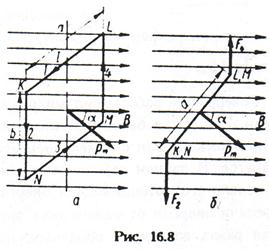
2. Прямокутна рамка KLMN із струмом I, поміщена в однорідне магнітне иоле індукції В (мал. 12.8, а). Пронумеруємо сторони рамки і позначимо сили, що діють на них з боку магнітного поля, F_1,F₂,F_3,F₄ ._.

Сили F₁ і F₃, прикладені до середин відповідних сторін, направлені протилежно і по формулі (12.12) рівні. Сили ж 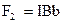и 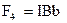створюють пару сил, момент якої (мал. 12.8, б)

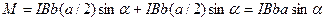(12.1.13)

Оскільки , то з (12.13} маємо

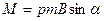•, (12.1.14)

або у векторній формі

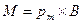• . (12.1.15)

Фактично на основі цієї залежності в § 12.1 була введена магнітна індукція.

Використовуючи закон Ампера, обчислимо роботу магнітного поля при переміщенні контура із струмом або зміні його форми.

При здійсненні силами F₂ і F₄ (рис 12.8, б) позитивної роботи (обертання рамки проти годинникової стрілки) кут а зменшується ( dа < 0 ), тому при обертанні рамки [див. (5.13)] 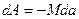або, враховуючи (12.14)

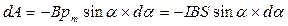(12.1.16)

(вважаємо, що при елементарному повороті dα сила струму I не змінюється). Диференціюючи (12.7), отримуємо

(12.1.17)

Зіставляючи (12.16) і (12.17), маємо

.

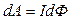Інтегруючи цю рівність, знаходимо роботу сил магнітного поля при переміщенні або деформації контура із струмом в полі:

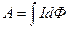(12.1.18)

Здійснення роботи силами поля означає зміна енергії контура із струмом. Це могло бути зміна енергії, пов'язаній з рухом контура (кінетична) або із зміною його положення (потенційна), або і те і інше. В даному випадку контур не прискорюється; отже, змінюється тільки його потенційна енергія в магнітному полі. Робота є міра передачі енергії від одного тіла іншому, тому елементарна робота сил поля рівна узятій із зворотним знаком елементарній зміні потенційній енергії контура із струмом в магнітному полі: dA=-dE_n Враховуючи (12.16), запишемо

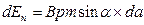. (12.1.19)

Інтегруючи цей вираз, отримуємо

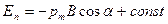( 12.1.20)

З умов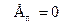и при 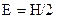знайдемо постійну в рівнянні:

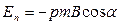. ( 12.1.21)

З формули (12.21) видно, що потенційна енергія контура в стійкій рівновазі (а = 0 ) мінімальна: 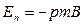, а при нестійкій рівновазі максимальна:

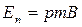
§ 12.3. ДІЯ МАГНІТНОГО ПОЛЯ НА РУХОМИЙ ЕЛЕКТРИЧНИЙ ЗАРЯД. СИЛА ЛОРЕНЦЯ

Сила, що діє, согласно.закону Ампера, на провідник із струмом В магнітному полі, є результат його дії на рухомі електричні заряди, що створюють цей струм.

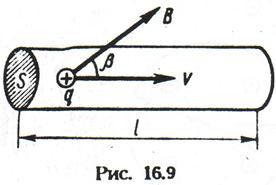
Розглянемо циліндровий провідник, довжиною l із струмом I, розташований в магнітному полі індукції В (мал. 12.9). Швидкість направленого руху деякого позитивного заряду g рівна v. Сила, що діє на окремий рухомий заряд, визначається відношенням сили F, прикладеної до провідника із струмом, до загального числа N носіїв струму в нім:

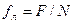(12.1.22)

Розкриємо вираз для сили, використовуючи (12.12) і вважаючи, що сила струму рівна

:

	Рис.12. 9

,

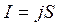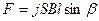де j - щільність струму. Враховуючи (15.1), отримуємо

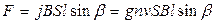, (12.1.23)

де 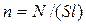- концентрація частинок.

Підставляючи (12.1.23) в (12.1.22), отримуємо

вираз для сили, що діє з боку магнітного поля на окремий рухомий електричний заряд і званою силою Лоренця:

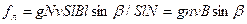• (12.1.24)

Напрям сили Лоренця можна визначити з векторного запису рівняння (12.1.24):

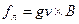( 12.1.25 )

Як видно з (12.25), ця сила завжди перпендикулярна площині, в якій лежать вектори V і В. Ізмеханіки відомо, що якщо сила перпендикулярна швидкості, то вона змінює лише її напрям, але не значення. Отже, сила Лоренця не змінює кінетичної енергії рухомого заряду і не здійснює роботи.

Якщо; заряд нерухомий щодо магнітного поля або його швидкість паралельна (антипараллельна) вектору магнітної індукції, то сила Лоренця рівна нулю. Її напрям [див. (12.25)] залежить від знаку заряду.

Хай в однорідне магнітне поле індукції B влітає із швидкістю V позитивно заряджена частинка (мал. 12.10). На неї діє сила Лоренця fл _, яка викличе доцентрове прискорення, і, по другому закону Ньютона

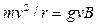( 12.1.26 )

де g і т - заряд і маса частинки; r - радіус траєкторії, по якій вона рухатиметься. З (12.26) отримуємо

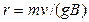(12.1.27)

Звідси витікає, що радіус траєкторії залишається постійним, а сама траєкторія є коло.

Використовуючи (12.27) і вважаючи, що значення швидкості частинки не змінюється, знайдемо період обертання її по колу:

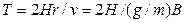
Відношення 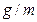називають питомим зарядом частинки. Період

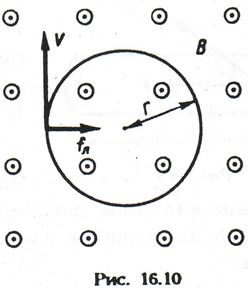обертання її в магнітному полі [див. (12.28)] не залежить від радіусу кола і швидкості, а визначається тільки магнітною індукцією і питомим зарядом. Цю особливість використовують в прискорювачі заряджених частинок - циклотроні.

Рис.12.10  

Щоб описати форму траєкторії зарядженої частинки, що влітає з швидкістю у в однорідне магнітне поле під довільним кутом до В (мал. 12.11), розкладемо вектор V на дві складові v _n и v _┴, направлені відповідно уздовж вектора магнітної індукції магнітного поля і перпендикулярно йому. Складова vn при русі частинки в магнітному полі залишається постійною;

сила Лоренця, що діє на частинку, змінить напрям v_┴.

Під дією цієї сили частинка обертається по колу. Таким чином, траєкторією руху буде гвинтова лінія - обертання по колу спільно з переміщенням уздовж вектора магнітної індукції із швидкістю vn _.

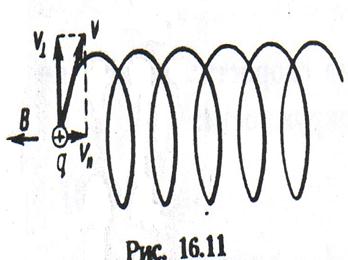
Якщо на рухому заряджену частинку g діють електричне поле з напруженістю E і магнітне поле з магнітною індукцією В (мал. 12.12), то результуюча сила рівна

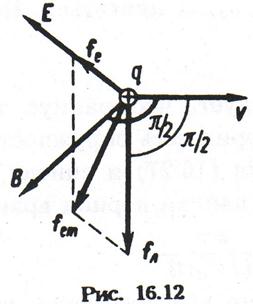
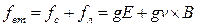. (12.1.29)

У багатьох системах (осцилограф, телевізор, електронний мікроскоп) здійснюють управління електронами або іншими зарядженими частинками, впливаючи на них електричними і магнітними полями, в цьому випадку основною розрахунковою формулою є (12.29).

Рис.12.11 Рис.12.12  

§ 12.4. ЕКСПЕРИМЕНТАЛЬНЕ ВИЗНАЧЕННЯ ПИТОМОГО ЗАРЯДУ ЧАСТИНОК

Вимірювання питомого заряду частинок дозволяє визначити масу атомів або молекул і ізотопний склад речовини. Розглянемо принцип дії однієї з пристроїв (мал. 12.13), використовуваних для цієї мети. Потік іонів однакового знаку пролітає через електричне і магнітне поля (вектор магнітної індукції усюди направлений від читача перпендикулярно площини креслення). Значення Е і В підбирають так, що поля діють на заряд g з силами, рівними по модулю, але протилежно направленими: 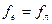або 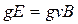, звідки

. (12.1.30)

Одні іони, швидкості яких задовольняють умові (12.30), не відхиляються полями і вилітають з отвору Про, інші ж відхиляються (штрихові лінії на малюнку) і затримуються. Таким чином, частина пристрою, зображеного на рис 12.13, є селектором швидкостей; змінюючи Е або В, можна відбирати з пучка іонів групи, що мають швидкості, визначувані умовою (12.30). Деякий розкид швидкостей обумовлений шириною отвору О.

Іони, що вилетіли з селектора Швидкостей, потрапляють в однорідне магнітне поле індукції В. Пролетая по напівокружних траєкторіях, вони залишають сліди на фотопластині Ф в різних місцях залежно від їх питомого заряду. По формулі (12.27) вычислим-удельные заряди іонів, що потрапили в різні місця фотопластини:

•

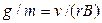
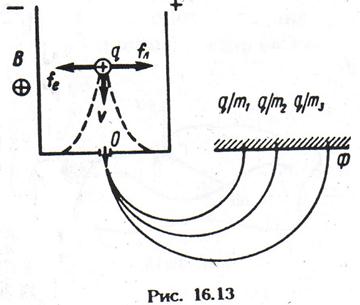После проявления на ней будут темные линии или пятна в местах попадания ионов, поэтому можно, во-первых, установить сам факт наличия ионов с определенным удельным заря­дом g/т или массой m, а во-вторых, по интенсивности линий - долю ионов с тем или иным значением удельного заряда.

Розглянутий прилад є одному з різновидів масс-спектрографа. Розділені іони в деяких випадках фіксують по

Рис.12.3  

струму, такий варіант приладу називають мас-спектрометром.

Масс-спектрографи і мас-спектрометри використовують для визначення ізотопного складу речовин.

§ 12.5. НАПРУЖЕНІСТЬ МАГНІТНОГО ПОЛЯ. ЗАКОН БІО-САВАРА - ЛАПЛАСА І ЙОГО ЗАСТОСУВАННЯ

У зв'язку з використанням поняття магнітної індукції виникає необхідність в обчисленні цієї характеристики магнітного поля залежно від конфігурації і значення струмів в якому-небудь середовищі. Таке завдання приводить до деякого допоміжного фізичного поняття - напруженості магнітного поля.

Хай в деякій крапці А створено магнітне поле контуром із струмом I (мал. 12.14). Якщо весь простір заповнений речовиною з відносною магнітною проникністю µ_r1, то в крапці А магнітна індукція буде В₁, що можна зміряти, наприклад, за допомогою пробної магнітної рамки. При заповненні всього простору іншою речовиною з відносною магнітною проникністю µ_r2 магнітна індукція в крапці А стане В₂. Продовжуючи цей досвід і заповнюючи простір різними речовинами, можна переконатися, що відношення 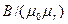або 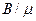(µ₀ - магнітна постійна, а .µ -абсолютна магнітна проникність) у всіх випадках однаково:

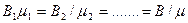. (12.1.32)

Відношення

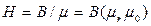• (12.1.33)

називають напруженістю магнітного поля. Вона не залежить від властивостей середовища, а визначається тільки силою струму, що протікає по контуру, і геометрією досвіду: формою контура і його розташуванням щодо точки А. Вектори Н і В співпадають по напряму.

Напруженість магнітного поля, створеного постійним струмом, можна обчислити, використовуючи закон Біо — Савара — Лапласа.

Рис.12.14 Рис.12.15  

Ж.Б. Біо і Ф. Савар встановили цей закон, експериментально визначивши дію струмів різної форми на магнітну стрілку. П.С. Лаплас проаналізував дані, отримані Біо і Сава ром, і знайшов, що напруженість магнітного поля будь-якого струму складається з напряженностей полів, що створюються його окремими елементами.

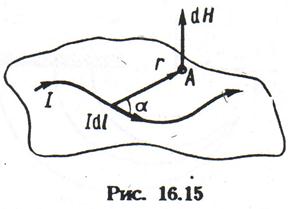
Візьмемо деякий провідник із струмом I виділимо елемент струму Idl з якого проведемо радіус-вектор r крапку А (мал. 12.15; а - кут між векторами (dl r ).В крапці А елемент струму створює магнітне поле, елементарна напруженість dH якого визначається законом Біо — Савара — Лапласа:

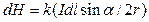•. (12.1.34)

Тут до - коефіцієнт пропорційності, залежний від вибору одиниць. У СІ k=1/(4π), тому

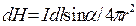• (12.1.35)

або у векторній формі

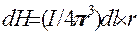(12.1.36)

З (12.36), за загальним правилом векторного твору, видно, що dН направлений перпендикулярно площині, вякій лежать вектори dl і r (мал. 12.15). Інтегруючи (12.36), знаходимо напруженість магнітного поля, створеного контуром із струмом або частиною цього контура:

(12.1.37)

Магнітне поле в центрі кругового струму. Кругом називають струм, що протікає по провідникові у формі кола. Цьому струму відповідає електричний заряд, що також обертається по колу.

Виділимо в круговому струмі елемент струму Idl і вкажемо напрям елементарній напруженості dH створеного їм магнітного поля в крапці Про - центрі кола (мал. 12.16). Для будь-якого елементу струму dН направлений уздовж пунктирної лінії, перпендикулярної площини струму, тому (12.37) можна записати вскалярній формі:

Рис.12.16 Рис.12.17  

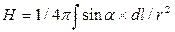
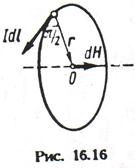
Враховуючи, що 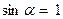, , 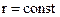отримуємо вираз для напруженості магнітного поля в центрі кругового струму:

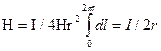(12.1.38)

Цю залежність можна використовувати, зокрема, для визначення одиниці напруженості магнітного поля - ампер на метр (А/м). Це напруженість в центрі кругового струму з діаметром, рівним 1 м, якщо по ньому протікає струм 1 А.

Знаючи напруженість магнітного поля і відносну магнітну проникність середовища, знаходимо магнітну індукцію:

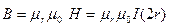• . (12.1.39)

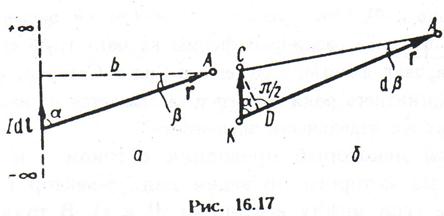
Магнітне нулі прямолінійного нескінченного провідника із струмом. Як деяка абстракція розглянемо необмежений прямолінійний провідник із струмом (мал. 12.17, а). Виділимо елемент струму Idl і проведемо радіус-вектор r в точку A, віддалену від провідника на відстань b. Вектор dH направлений перпендикулярно площини малюнка від читача. З малюнка видно, що від будь-якого елементу струму елементарна напруженість магнітного поляв крапці А перпендикулярна площині креслення, тому, як і в попередньому прикладі, (12.37) можна записати в скалярній формі:

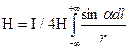
Перетворимо подынтегральное вираз так, щоб в нього входила тільки одна змінна - кут α. З мал. 12.17, а знаходимо 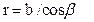і 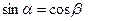(16-41)

На мал. 12.17, 6 показаний в більшому масштабі кут, під

яким з крапки А видно вектор dl. З ∆САD витікає, що | 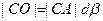; оскільки приблизно , то

. З ∆CDK маємо

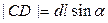; отже, 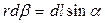звідки 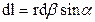. Підставляючи (12.1.41) в останню рівність, отримуємо

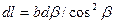. (12.1.42)

Враховуючи (12.42), перетворюваний (12.40):

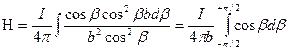
Межі інтеграції відповідають крайнім значенням утла: ± H/2. Інтегруючи, знаходимо вираз для напруженості магнітного поля, створеного нескінченним прямолінійним провідником із струмом в будь-якій крапці, віддаленій від провідника на відстань b:

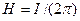(12.1.43)

§ 12.6. ЗАКОН ПОВНОГО СТРУМУ. НАПРУЖЕНІСТЬ МАГНІТНОГО ПОЛЯ СОЛЕНОЇДА

У ряді випадків для визначення напруженості магнітного поля разом із законом Біо — Савара — Лапласа доцільно використовувати пов'язаний з ним закрн повного струму.

Проведемо лінії напряженности магнітного поля, створеного нескінченним прямолінійним провідником із струмом в площині, перпендикулярній провідникові, у вигляді концентричних кіл (мал. 12.18). Ради спрощення як довільний контур виберемо коло радіусом b, співпадаючу з однією з ліній Н. Так як контур і лінія напруженості однакові формою, то

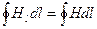(12.1.44)

Для обчислення циркуляції підставимо сюди формулу (12.43):

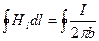
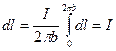, т.е.

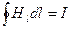• (12.1.45)

Це закон повного струму, який зв'язує циркуляцію вектора напруженості магнітного поля і силу струму.

Складніший розрахунок міг би показати, що формула (12.45) справедлива для довільного контура, що охоплює будь-які струми. Зазвичай цей закон записують у вигляді

Рис.12.18 Рис.12.19 12.20  

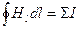
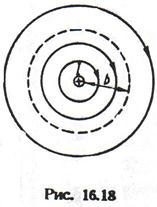
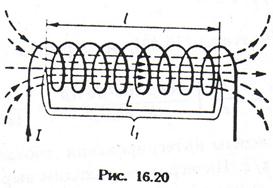
Циркуляція вектора напруженості магнітного поля по контуру рівна сумі алгебри струмів, що охоплюються цим контуром.

Наприклад, якщо контур охоплює три струми (мал. 12.19): 1 і 2 -позитивні

3 - негативний, - те закон повного струму для цього випадку має вигляд

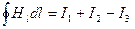
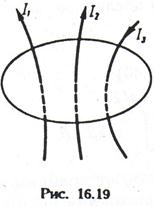
Застосуємо закон повного струму і знайдемо напруженість магнітного поля соленоїда (мал. 12.20; пунктиром показані лінії напруженості). Чим довше соленоїд і менше його діаметр, тим більше однорідно усередині нього магнітне поле. Рахуватимемо поле усередині соленоїда однорідним, а поза соленоїдом - достатньо слабким. Хай l - довжина соленоїда; N - загальне число витків; n = N/l -отношение числа витків до довжини соленоїда (щільність намотування). Проведемо на мал. 12.20 довільний контур L, для якого розраховується циркуляція. Одна його частина, l, співпадає з лінією Н усередині соленоїда, інша, l1 - проходить поза ним. Таким чином, циркуляція може бути представлена двома інтегралами:

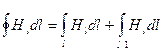(12.1.47)

Оскільки усередині соленоїда 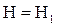, то 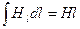поза соленоїдом H мало, тому з (12.47) маємо 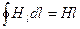. Використовуючи закон повного струму (12.46), отримуємо 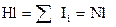звідки

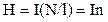. (12.1.48)

Це означає, що напруженість магнітного поля соленоїда рівна твору сили струму на число витків, віднесених до довжини соленоїда.

І: integer;

X, У, X1, Х2: real;

writeln ('Значення функции Ехр(-|Х|) ');

Writeln;

Writeln ('Введите интервал значений аргумента: X1, Х2 ');

Readln (XI, Х2);

for І:=1 to 10 do

Х:=Х1+(Х2-ХІ)*(1-1)/9;

у:=Ехр(-Аbs(Х));

Writeln (У);

end;

У розділі опису змінних зазначено параметр циклу і (тип integer), а також змінні аргументу X і функції У, межі інтервалу X1 і Х2 (тип real). На початку виконання програми на екрані з'являється напис «Значення функції Ехр (-Аbs (х))», а потім у процесі циклічних обчислень виводиться стовпчик значень Y.

Оператор WHILE («цикл-поки»)

Оператор циклу While, як і оператор for, розглядався в главі, присвяченій мові Бейсік. Нагадаємо, що він є оператором циклу з передумовою («цикл-поки»), оскільки перевірка умови здійснюється при кожному повторенні перед виконанням тіла циклу. Оператор While має такий формат запису:

<змінна>:=<P1>;

While <умова> do

begin

< тіло циклу >;

<змінна>:=<змінна>+<N>;

Умова є логічним виразом, а тіло циклу - оператором, який може бути простим чи складеним. Перед кожним виконанням тіла циклу обчислюється значення умови. Якщо значенням буде True, цикл виконується і знову обчислю­ється умова. Так повторюється, поки умова не дасть значення Faste і не відбудеться вихід з циклу та передача керування наступному оператору про­грами.

Виконання:

1.Змінній циклу присвоюється початкове значення

2.Перевіряється умова

3.Якщо умова правильна, то виконується тіло циклу

4.Якщо умова неправильна, то виконання циклу припиняється

5.Значення змінюється на значення кроку N

Наведемо приклад використання оператора WHILE. Знайдемо за допомогою його залишок від ділення двох цілих чисел А і B, не звертаючись до операції mod.

program RES;

А, В, X: integer;

Writeln ('Введите А, В');

Readln (А, В);

Х:= А;

While Х>=В do

X:=X-B;

Writeln ('Остаток от деления равен’,Х);

end.

Як тіло циклу тут використано простий оператор X: =Х-В;.

Оператор While дозволяє складати компактні програми для обчислення різних сум послідовностей чисел. Нехай потрібно обчислити суму ряду

S = X + X² +... + Х^N при довільному значенні X. Запишемо для цього програму.

Program Sum;

var

І, N:integer;

X, У, S: real;

begin

Writeln ('Введите X, N');

Readln (X, N);

І:=1; Y:=1; S:=0;

While І<=N do

Begin

Y:=Y*Х;

S:=S+Y;

І:=I+1;

end;

Writeln (^‘Сумма равна: ', S);

end.

Зверніть увагу, що роботою циклу While «диригує» оператор і: =1 + 1, названий лічильником циклів. Поки значення лічильника не перевищує N, цикл триває. Значення лічильника, що дорівнює N + 1, припиняє роботу оператора While.

Оператор repead («цикл-до»)

Ще одну конструкцію циклу представляє оператор repead, що записується так:

<змінна>:=<P1>;

REPEAT

<тіло циклу>;

<змінна>:=<змінна>+<N>;

UNTIL <умова>;

Цей оператор організує циклічні обчислення таким чином, що умова пере­віряється після чергового виконання тіла циклу. Якщо вираз умови набуває значенняTrue, повторення припиняються. Тому оператор repeat називають ще циклом з постумовою чи просто - «циклом-до» (робота циклу триває, поки не виконана умова завершення).

Оператор repeat (як і оператор While) дозволяє виконувати повторювані дії, коли число повторень заздалегідь не відомо. Розглянемо як приклад спадну геометричну прогресію (q<1):

1, q, q^г,..q,..

Як відомо, сума членів цієї нескінченної прогресії дорівнює 1/ (1-q). Скла­демо програму, за допомогою якої можна було б перевірити цю формулу на конкретних прикладах.

Побудуємо алгоритм таким чином, щоб обчислення суми припинялося, як тільки останній член у цій сумі буде менший деякої заздалегідь заданої величини

Е (наприклад, Е=0.0 001). У наступній програмі виконується введення значень q, Е і додавання членів прогресії за допомогою оператора repeat:

program Progression;

І, N: integer;

Q, Y, S, Е: real;

writeln ('Введите Q');

readln (Q);

writeln ('Введите границу для последнего учитываемого члена прогрессии');

readln (Е);

Y:=1; S:=1;

Y:=Y*Q;

S:=S+Y;

end;

ABS(Y)<=Е;

Writeln ('Сумма = ',5:8:6);

Поняття масиву, оголошення та ініціалізація масивів, базові операції при роботі з масивами.

Масив даних – це структура, яка дає змогу зберігати в оперативній памяті компютера значну кількість даних одного типу. Розглянемо приклади числових даних однакового типу:

- Значення температур, які булт протягом деякого місяця;

- Оцінки учнів;

- Обсяг продукції ложного місяця протягом року.

Приклади текстових масивів: список учнів класу, назви кінотеатрів міста, назви видів продукції. Такі масиви даних називають лінійними таблицями, або одновимірними масивами.

Імена масивам надає користувач.

Масиви опрацьовують поелементно. Доступ до елемента забезпечується виразом, що складається з імені масиву та індексу.

Приклад: Т[1] – це перший елемент масиву Т, T[i] – це i-й елемент Т.

Опис типів масивів та оголошення змінних типу массивів.

Тип масиву описують так:

type <назва типу>=array[<розмір>] of <назва базового типу>

type Massi = array [1..20] of real;

Конкретні масиви оголошують командою так:

var <список імен масивів>: < назва типу масивів

Об’єднавши опис типу й оголошення змінних в одну команду:

var <список імен масивів>: array[<розмір>] of <назва базового типу>

var М: array[1..20] of real;

Формування масиву.

Вивести на екран монітора заданий масив із 20 цілих чисел у стовпчик.

Program mas;

║Var

║ a: array [1..20] of integer;

║ i:integer;

║begin

║ for i:=1 to 20 do

║ read (A[ i ]);

║ for i:=1 to 20 do

║ writeln (A[ i ]);

║end.

Дата добавления: 2014-01-04