Размещения без повторений

Основные формулы комбинаторики

ЛЕКЦИЯ 2

При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества. При решении задач комбинаторики используют следующие правила:

Правило суммы: если объект А может быть выбран m способами, объект В может быть выбран n способами, то «А или В» может быть осуществлен m + n способами.

Правило произведения: если объект А может быть выбран m способами и после каждого такого выбора объект В может быть выбран n способами, то «А и В» в указанном порядке может быть осуществлен m · n способами.

Задача 1. В магазине имеются три куклы и четыре машины. Сколькими способами можно выбрать подарок, состоящий из одной игрушки?

Решение. Подарок может быть куклой или машиной, куклу можно выбрать тремя способами, а машину – четырьмя, следовательно, число способов равно 3 + 4 = 7.

Задача 2. Сколькими способами можно выбрать подарок из двух игрушек (куклу и машину)?

Решение. Куклу можно выбрать тремя способами, а машину – четырьмя. Следовательно, всего число способов выбрать куклу и машину равно: 3 · 4 = 12.

Рассмотрим следующие виды комбинаций: размещения без повторений и с повторениями, перестановки без повторений и с повторениями, сочетания без повторений и сочетания с повторениями. Комбинаторика позволяет не только определить вид комбинации, но и подсчитать количество таких комбинаций.

Определение. Размещением из п элементов по k называется любое упорядоченное множество, содержащие k элементов из данных n, то есть k ≤ n. Число всех возможных размещений обозначают символом .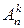

Теорема. Число всех размещений находится по формуле:

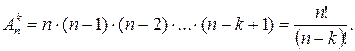
Задача 3. Предположим, в соревнованиях участвуют 20 спортсменов. Разыгрывается золотая, серебряная и бронзовая медали. Сколькими способами могут определиться призеры?

Решение. Нужно сначала определить тройку призеров. Кроме того, медали среди них могут быть распределены по-разному. Таким образом, речь идет об упорядоченных наборах из трех элементов. Число таких наборов:

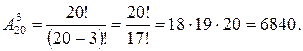
Задача 4. Сколько возможно различных вариантов пьедестала почета (первое, второе, третье места), если в соревнованиях принимают участие 10 человек?

Решение.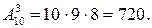

Дата добавления: 2014-01-04