Локальная и интегральная формулы Лапласа

Пользоваться формулой Бернулли при больших значениях n достаточно трудно, так как формула требует выполнения действий над очень большими числами.

Пример. Если , , ; 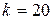, то вероятность того, что при n испытаниях событие A осуществляется ровно раз и не осуществляется, раз примет вид: .

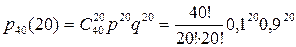При вычислении факториала для больших чисел можно пользоваться специальными таблицами логарифмов факториалов, но из-за округлений в итоге окончательный результат может значительно отличаться от истинного. В этом случае удобно пользоваться формулами Лапласа.

Локальная теорема Лапласа. Если вероятность 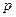появления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие A появиться в испытаниях ровно раз, приближенно равна (тем точнее, чем больше 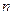) значению функции:

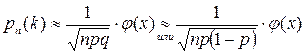(1) – локальная формула Лапласа,

где , .

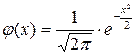Замечание. При нахождении значений функции 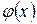для отрицательных значений аргументов следует иметь в виду, что 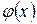– четная функция: .

Для вычисления значений функции 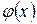пользуются специальной таблицей (см. Приложение 2).

Задача 1. Найти вероятность того, что при 400 испытаниях событие наступит ровно 104 раза, если вероятность его появления в каждом испытании равна 0,2.

Решение. По условию, ; ; 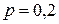, тогда q = 1 – 0,2 = 0,8. Применим локальную формулу Лапласа:

; .

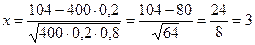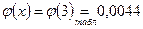Тогда .

Интегральная теорема Лапласа. Если вероятность p наступления события A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность 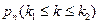того, что событие Aпоявится в nиспытаниях от k₁ до k₂ раз, приближенно равна: 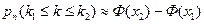(2),

где , , 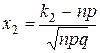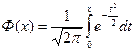– «неберущийся» интеграл.

Функция 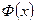называется функцией Лапласа, при решении используют соответствующую таблицу значений для функции 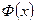(см. Приложение 3).

Замечание. При нахождении значений функци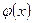и и 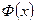для отрицательных значений аргументов следует иметь в виду, что 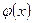– четная: 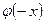=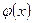, а 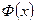– нечетная: = .

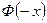Отметим еще, что приближенными формулами Лапласа (1) и (2) на практике пользуются в случае, если npq ³ 10. Если же npq < 10, то эти формулы приводят к довольно большим погрешностям.

Задача 2. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах мишень будет поражена:

а) не менее 70 и не более 80 раз;

б) не более 70 раз.

Решение.

а) По условию k ₁ = 70, k ₂ = 80, 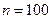, 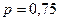. Тогда ,

, ,

.

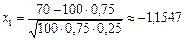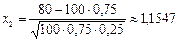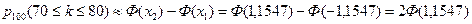Значение функции Лапласа находим по таблице. Мы получили значение 1,1547, в таблице даны значения Ф (1,15) = 0,3749 и Ф (1,16) = 0,3770. В качестве ответа можно взять любое из этих значений или их среднеарифметическое { ответ будет приблизительно одинаковый }:

р ₁₀₀(70;80)» 2Ф(1,1547)» 2(Ф(1,15) + Ф(1,16))/2 = 0,7519.

б) По условию k ₁ = 0, k ₂ = 70. Тогда

,

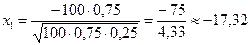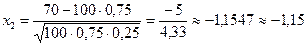
р ₁₀₀()» Ф (x ₂) – Ф (x ₁) = Ф (–1,1547) – Ф (–17,32) = Ф (17,32) – Ф (1,1547).

Значение функции Лапласа находим по таблице. В таблице приведены значения интеграла лишь для 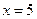, тогда для можно принять значение функции Лапласа .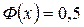

р ₁₀₀(0;70)» 0,5 – 0,3749 = 0,1251.

Дата добавления: 2014-01-04