
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Общие сведения о свойствах и движении жидкостей и газов
|
|
|
|
Многие важные процессы, протекающие в промышленных печах, зависят от характера движения газов (теплообмен, распределение температур и давлений и др.). В топливных печах продукты сгорания топлива являются тем теплоносителем, от которого теплота передается обрабатываемому материалу. В электрических печах движение воздуха или специально созданной атмосферы способствует развитию теплообменных процессов. Влияние, которое оказывает движение газов на работу печи в целом и есть та причина, по которой движение (механика) газов является одним из важнейших разделов металлургической теплотехники.
Свойства жидкостей и газов
1.3.1.Жидкости и газы.
Гидромеханика и механика газов рассматривают жидкость и газ как сплошную легкоподвижную среду, в которой отсутствует молекулярное движение, а распределение вещества и физических свойств происходит непрерывно. Такие среды разделяют на среды несжимаемые (собственно жидкости) и среды сжимаемые (собственно газы). Однако это не всегда точно, так как капельные жидкости в ряде случаев обладают некоторой способностью сжиматься, а газы во многих практических случаях можно рассматривать как несжимаемые. Газы в печах находятся под давлением, которое менее чем на 0,2 % отличается от атмосферного. В этих условиях возможное изменение объема вследствие изменения давления ничтожно. Температура в печах в подавляющем большинстве случаев изменяется постепенно, что дает основание на отдельных участках пренебрегать влиянием температуры на объем газа и рассматривать газы как несжимаемые среды. Общим признаком несжимаемости газов является условие  . Поэтому в механике газов используются положения гидромеханики, гидравлики и аэродинамики. Явление сжимаемости газов проявляется при высоких (сверхзвуковых) скоростях движения. В этих условиях
. Поэтому в механике газов используются положения гидромеханики, гидравлики и аэродинамики. Явление сжимаемости газов проявляется при высоких (сверхзвуковых) скоростях движения. В этих условиях 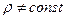
1.3.2.Газы реальные и идеальные.
Всем жидкостям и газам присуще свойство вязкости, т. е. способность оказывать сопротивление относительному движению (перемещению) частиц. Однако в некоторых газах (кислород, азот, оксид и диоксид углерода и др.) свойство вязкости проявляется слабо и им без большой погрешности можно пренебречь. Это послужило причиной того, что было предложено и применено понятие идеального газа (идеальной жидкости) — абстрактной среды, лишенной свойства вязкости.
В реальных газах молекулы подвержены силам взаимодействия и эти газы обладают вязкостью, т. е. свойством оказывать сопротивление относительному движению (перемещению) частиц. При движении газов свойство вязкости проявляется в возникновении сил внутренного трения. Поэтому перемещение газов связано с затратой энергии. Силу трения при движении газов (рис. 1) можно подсчитать по формуле Ньютона 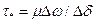 ,
,
|

 где
где 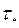 — сила трения, отнесенная к единице поверхности, разделяющей слои газа, Н/м2; (
— сила трения, отнесенная к единице поверхности, разделяющей слои газа, Н/м2; ( — коэффициент пропорцииональности, называемый коэф-фициентом динамической вяз-кости, Па∙с;
— коэффициент пропорцииональности, называемый коэф-фициентом динамической вяз-кости, Па∙с; 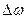 — разность скоростей на границах слоя толщиной
— разность скоростей на границах слоя толщиной  . Наряду с коэффициентом динамиче-ской вязкости в механике газов пользуются коэффи-циентом кинематической вязкости
. Наряду с коэффициентом динамиче-ской вязкости в механике газов пользуются коэффи-циентом кинематической вязкости  , м2/с
, м2/с  =
= , где
, где 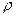 — плотность газа, кг/м3.
— плотность газа, кг/м3.
С увеличением температуры вязкость газов растет. Наличие вязкости и, как следствие, трения в реальных газах при их движении приводит к возникновению непосредственно около поверхности так называемого пограничного слоя, толщина которого составляет примерно 1 % всей толщины потока. В этом тонком слое жидкости происходит резкое изменение скорости от скорости потока на его внешней поверхности до нуля непосредственно на стенке. Несмотря на незначительные (относительно всего потока) размеры, пограничный слой играет огромную роль как в процессах гидро- и аэродинамики, так и в процессах теплообмена.
1.3.3.Статика и динамика газов.
В металлургических печах встречаются такие случаи, когда заполняющий объем нагретый газ находится в покое. В этом случае используются закономерности статики газов.
Однако гораздо более распространенным является движение газов (динамика газов).
В рабочем пространстве печей и дымовых каналах газ обычно движется при относительно невысоких скоростях (до 70 – 80 м/с) и небольших перепадах давления (до 100 Па). Изменение давления такого порядка практически не влияет на плотность газа, поэтому в этих случаях все рассуждения ведутся при постоянной плотности. Однако возможно ощутимое изменение плотности в зависимости от температуры. Поэтому расчет обычно ведут, используя величину плотности, полученной на данном участке по среднеарифметической температуре газа и принимаемой неизменной. В отдельных элементах печей (в форсунках, горелках) встречается движение газов с высокой скоростью, причем возможная величина скорости может изменяться в очень широких пределах: от 150—200 м/с до скорости звука и выше. При таких скоростях, связанных с большими перепадами давления, принимать плотность газа постоянной недопустимо.
Поэтому ниже рассматриваются закономерности движения газов как с низкой ( , несжимаемые газы), так и с высокой скоростью (
, несжимаемые газы), так и с высокой скоростью ( , сжимаемые газы).
, сжимаемые газы).
Вместе с тем скорость движения газов оказывает влияние и на характер движения потока, который может быть различным.
1.3.4.Турбулентное и ламинарное движения
В зависимости от характера движения различают ламинарное (или слоистое), турбулентное (или вихреобразное) и переходное (неустановившееся) движения газов. Ламинарным называется такое движение, при котором струйки газа перемещаются параллельно одна другой, не пересекаясь.
Характерной особенностью ламинарного движения является параболическое распределение скоростей по сечению потока, обусловленное трением о поверхность прилегающего к ней слоя газа и последующих слоев друг о друга (рис. 2).
При турбулентном режиме в потоке возникает множество вихрей, что приводит к интенсивному перемешиванию газа. Распределение скоростей при этом более равномерно и имеет вид усеченной параболы.
Пределы существования ламинарного и турбулентного движения были установлены О. Рейнольдсом (1883 г.), который показал, что характер движения зависит от соотношения сил инерции и сил внутреннего трения. Это соотношение характеризуется безразмерным комплексом, названным впоследствии критерием Рейнольдса:  , где
, где 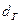 – гидравлический диаметр канала. (Для каналов произвольной формы
– гидравлический диаметр канала. (Для каналов произвольной формы  , где
, где – площадь сечения;
– площадь сечения;  – периметр).
– периметр).
Установлено, что ламинарное течение имеет место при малых значениях критерия Рейнольдса, а турбулентное при относительно более высоких. Так, для случая течения жидкости в круглых трубах при Re<2100 поток ламинарный, при Re>10000 поток турбулентный. Интервал 2100< Re <10000 соответствует неустановившемуся движению. Из структуры критерия Рейнольдса видно, что турбулизации потока способствуют увеличение скорости и диаметра канала и препятствует увеличение коэффициента кинематической вязкости.

|
При течении какой-то вполне определенной жидкости (газа) по каналу постоянного сечения характер потока зависит исключительно от скорости. При увеличении скорости поток может перейти из ламинарного в турбулентный, и наоборот.
Если обратить внимание на эпюру распределения скоростей при турбулентном пристеночном движении (см. рис. 2), то видно, что все сечение потока может быть разделено на две не равные части: очень тонкий, пристеночный пограничный слой и основная часть потока. В пределах пограничного слоя резко изменяется (уменьшается к поверхности) скорость, а в пределах основного потока скорость практически неизменна.
Таким образом, при турбулентном движении основной части потока, где скорость практически неизменна, характерно отсутствие трения, т. е. в этой части потока вязкость среды на движение не влияет и можно применять закономерности, полученные для идеальной среды. Это обстоятельство является одной из причин использования понятия идеальной среды, с помощью которого получено много практических решений, в частности в аэродинамике. В тех случаях, когда нельзя ограничиться рассмотрением только основной части турбулентного потока, приходится анализировать картину явлений в пограничном слое на основе теории пограничного слоя, получившей к настоящему времени значительное развитие. Пограничный слой оказывает большое влияние не только на характеристики движения, но и на теплообмен между потоком газа и окружающей поверхностью.
При ламинарном движении пограничный слой всегда ламинарный. В ламинарном потоке теплота передается исключительно теплопроводностью, в турбулентном — теплопроводностью и конвекцией со значительным преобладанием последней. Поэтому при теплообмене между турбулентным потоком газа и поверхностью передача теплоты через пограничный слой является наименее интенсивной и потому определяющей.
1.3.5. Давление газов
Давление есть сила, действующая на единицу площади. Различают давление абсолютное и избыточное. Избыточное давление представляет собой разницу между давлением в какой-то емкости и атмосферным. Если это давление меньше атмосферного (отрицательное избыточное давление), то его называют разрежением.
В металлургической теплотехнике пользуются избыточным (над атмосферным) давлением. Различают три основных вида: геометрическое, пьезометрическое и скоростное (динамическое) давления.
Геометрическое давление обусловлено стремлением горячих газов подняться вверх. Если в результате разности плотностей окружающего воздуха и газа последний переместится на высоту 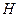 , то геометрическое давление
, то геометрическое давление
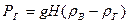 , (3)
, (3)
где 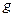 — ускорение силы тяжести, м/с2;
— ускорение силы тяжести, м/с2;  и
и 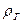 — плотность соответственно воздуха и газа, кг/м3;
— плотность соответственно воздуха и газа, кг/м3; 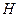 —расстояние (высота), на которое переместился газ, м.
—расстояние (высота), на которое переместился газ, м.
Пьезометрическое давление (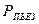 ) – есть разность давлений заключенного в сосуде газа и окружающей среды. Оно может быть как положительным, так и отрицательным. Его величина определяется непосредственно из опыта с помощью U-образного манометра (пьезометра). Манометр надо устанавливать так, чтобы один конец его сообщался с атмосферой, а выходное отверстие другого конца было расположено перпендикулярно направлению потока газа (рис. 3).
) – есть разность давлений заключенного в сосуде газа и окружающей среды. Оно может быть как положительным, так и отрицательным. Его величина определяется непосредственно из опыта с помощью U-образного манометра (пьезометра). Манометр надо устанавливать так, чтобы один конец его сообщался с атмосферой, а выходное отверстие другого конца было расположено перпендикулярно направлению потока газа (рис. 3).
Скоростное давление наблюдается при движении газа. Оно равно:
 (4)
(4)
Скоростное давление также может быть определено непосредственно из опыта (рис. 4). Для этого один конец манометра подсоединяют перпендикулярно, а другой – навстречу направлению потока. Сумма пьезометрического и скоростного давлений составляет полное давление 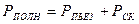 , которое и вос-
, которое и вос-


|
|
принимается трубкой, помещенной навстречу потоку. Но поскольку
 , (5)
, (5)
то манометр в этом случае показывает величину скоростного давления.
Сумма геометрического и пьезометрического давления называется статическим и характеризует тот запас потенциальной энергии, которым располагает 1 м3 газовой системы. Скоростное давление — это часть кинетической энергии потока. В процессе движения газа на преодоление всевозможных сопротивлений затрачивается часть кинетической энергии, убыль которой восстанавливается за счет запаса потенциальной энергии. Эти процессы протекают одновременно, в результате чего приборами фиксируются лишь конечный результат, т. е. изменение энергии газа (изменение статического давления).
1.3.6.. Статика газов
|

 Статика газов изучает равновесие (состояние покоя) жидкостей и газов. Основой раздела механики сплошных сред являются уравнения Эйлера, получаемые при составлении баланса сил, действующих на каждый элементарный объем покоящейся жидкости или газа. Все силы, действующие на объем газа (жидкости), можно разделить на объемные и поверхностные. К объемным относятся силы, действующие на каждую частицу объема: силы тяжести и силы инерции. Поверхностные силы действуют на единицу поверхности какого-то объема. Такими силами являются силы давления и трения. На любой объем покоящейся жидкости или газа действуют только силы тяжести и давления. Силы инерции и трения проявляются лишь при движении среды. Поэтому уравнения Эйлера для статики справедливы для идеальной и реальной жидкости (газа), так как свойство вязкости, характерное для реальной среды, проявляется только при ее движении. В неподвижном (покоящемся) объеме газа объемные силы — силы тяжести — действуют по вертикали, т. е. в направлении координатной оси z, и вызывают соответствующее изменение давления.
Статика газов изучает равновесие (состояние покоя) жидкостей и газов. Основой раздела механики сплошных сред являются уравнения Эйлера, получаемые при составлении баланса сил, действующих на каждый элементарный объем покоящейся жидкости или газа. Все силы, действующие на объем газа (жидкости), можно разделить на объемные и поверхностные. К объемным относятся силы, действующие на каждую частицу объема: силы тяжести и силы инерции. Поверхностные силы действуют на единицу поверхности какого-то объема. Такими силами являются силы давления и трения. На любой объем покоящейся жидкости или газа действуют только силы тяжести и давления. Силы инерции и трения проявляются лишь при движении среды. Поэтому уравнения Эйлера для статики справедливы для идеальной и реальной жидкости (газа), так как свойство вязкости, характерное для реальной среды, проявляется только при ее движении. В неподвижном (покоящемся) объеме газа объемные силы — силы тяжести — действуют по вертикали, т. е. в направлении координатной оси z, и вызывают соответствующее изменение давления.
Уравнение Эйлера для статики жидкостей и газов, составленное как баланс изменения энергии 1 м3 газа в направлении координатной оси z, имеет вид
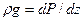 , (6)
, (6)
где 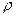 — плотность жидкости (газа), кг/м3; g — ускорение силы тяжести, м/с2;
— плотность жидкости (газа), кг/м3; g — ускорение силы тяжести, м/с2;  — изменение (приращение) давления при изменении высоты столба жидкости на величину
— изменение (приращение) давления при изменении высоты столба жидкости на величину 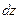 ;
;  — градиент давления.
— градиент давления.
Уравнение (6) представляет собой баланс энергии, при котором изменение потенциальной энергии 1 м3 газа на отрезке dz (левая часть уравнения) приводит к соответствующему изменению давления (правая часть уравнения).
Если уравнение Эйлера (6) решать для каких-то двух сечений z1 и z2 (рис. 5), расположенных на расстоянии H друг от друга, при условии  (газ как несжимаемая жидкость), то можно получить основное уравнение статики жидкостей (газов):
(газ как несжимаемая жидкость), то можно получить основное уравнение статики жидкостей (газов):
 , (7)
, (7)
где 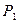 и
и  — абсолютные давление соответственно в сечениях
— абсолютные давление соответственно в сечениях и
и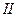 , Па;
, Па;  — геометрическое давление, обусловленное силой тяжести и зависящее от плотности
— геометрическое давление, обусловленное силой тяжести и зависящее от плотности 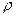 и высоты
и высоты 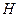 столба газа, Па;
столба газа, Па;  и
и  — расстояние от произвольно принятого уровня отсчета 0 — 0 до соответственно сечений
— расстояние от произвольно принятого уровня отсчета 0 — 0 до соответственно сечений  и
и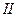 , м;
, м; 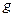 — ускорение силы тяжести, м/с2.
— ускорение силы тяжести, м/с2.
Как следует из определения, приведенного выше, разность между абсолютным давлением  газа в сосуде и давлением
газа в сосуде и давлением  воздуха на том же уровне является пьезометрическим давлением.
воздуха на том же уровне является пьезометрическим давлением.
Если давление газа в сосуде меньше атмосферного, это означает, что сосуд находится под разрежением. Величина разрежения показывает, на сколько абсолютное давление газа в сосуде меньше атмосферного, т. е.
 . (8)
. (8)
Поверхность, в каждой точке которой пьезометрическое давление равно нулю ( ), называют уровнем нулевого избыточного давления.
), называют уровнем нулевого избыточного давления.
Для печной теплотехники важное значение имеет исследование распределения избыточного давления на стенки сосуда, заполненного горячим газом (рис. 6). Величину избыточного давления на стенки сосуда можно найти с помощью основного уравнения статики газов (7).
Рассмотрим, как определить пьезометрическое давление применительно к сосуду, открытому снизу (рис. 6,а). В сечении  сосуд сообщается с атмосферой, поэтому давление со стороны газа
сосуд сообщается с атмосферой, поэтому давление со стороны газа  равно давлению со стороны воздуха
равно давлению со стороны воздуха  и, следовательно,
и, следовательно,  .
.

Рис. 6. Изменение избыточного давления по высоте сосуда
а- открытого снизу; б- открытого сверху

Рис. 7. Распределение давления горячего газа
по высоте рабочего пространства печи
В сечении 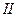 давление со стороны газа
давление со стороны газа 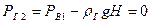 , а со стороны воздуха
, а со стороны воздуха  . Пьезометрическое давление в сечении
. Пьезометрическое давление в сечении 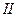
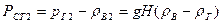 . Из этого уравнения видно, что при
. Из этого уравнения видно, что при 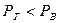 стенки сосуда испытывают избыточное давление со стороны газа, величина которого прямо пропорциональна высоте
стенки сосуда испытывают избыточное давление со стороны газа, величина которого прямо пропорциональна высоте 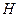 и разности плотностей воздуха
и разности плотностей воздуха 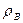 и газа
и газа 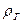 . Избыточное давление, обусловленное разностью плотностей воздуха и газа, есть геометрическое давление
. Избыточное давление, обусловленное разностью плотностей воздуха и газа, есть геометрическое давление  , которое в данном случае равно
, которое в данном случае равно
 . (9)
. (9)
Для сосуда, открытого сверху (рис. 7, б), давление газа в сечении  равно давлению атмосферного воздуха, следовательно:
равно давлению атмосферного воздуха, следовательно:
 .
.
Применяя уравнение (7), получаем
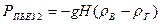
или
 .
.
.Это означает, что при 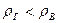 избыточное давление в сосуде будет отрицательным, т.е. сосуд будет находиться под разряжением
избыточное давление в сосуде будет отрицательным, т.е. сосуд будет находиться под разряжением 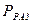 , абсолютное значение которого равно
, абсолютное значение которого равно  , т.е.
, т.е.  . Избыточное давление, обусловленное разностью плотностей воздуха и газа, играет важную роль в печах. Если нулевое давление (
. Избыточное давление, обусловленное разностью плотностей воздуха и газа, играет важную роль в печах. Если нулевое давление ( ) находится на уровне пода (рис. 7), то над уровнем пода давление в печи больше атмосферного. Это приводит к выбиванию горячих газов через отверстия и неплотности в стенках печи, что в свою очередь ухудшает условия службы металлических конструкций печи и вызывает перерасход топлива.
) находится на уровне пода (рис. 7), то над уровнем пода давление в печи больше атмосферного. Это приводит к выбиванию горячих газов через отверстия и неплотности в стенках печи, что в свою очередь ухудшает условия службы металлических конструкций печи и вызывает перерасход топлива.
Если нулевое давление поддерживать несколько выше уровня пода, то часть печи, расположенная ниже нулевого давления, будет находиться под разрежением, что вызовет подсос холодного воздуха в печь. Холодный воздух, помимо перерасхода топлива, снижает температуру печи и увеличивает угар (окисление) металла. При нагреве металла вред от подсоса воздуха больше, чем от выбивания газов из печи, поэтому, чтобы исключить подсос воздуха в печь, нулевое давление поддерживают на уровне пода или немного ниже, а для уменьшения выбивания газов из печи печь делают более герметичной.
1.3.7. Динамика газов. Элементы теории движения реальных газов
При движении газа на каждый его объем будут действовать не только те силы, которые характерны для статики, но и другие, сильно усложняющие как явление в целом, так и его математическое описание. Для движения идеального газа этими дополнительными силами будут силы инерции, а для реального газа — силы инерции и трения (вязкости). В механике сплошных сред большое внимание уделяется выводу и использованию соответствующих математических уравнений, описывающих движение идеальных (уравнения Эйлера) и реальных сред (уравнения Навье — Стокса). Уравнения Навье — Стокса настолько сложны, что к настоящему времени решены лишь для крайне ограниченного числа случаев. Эта сложность вызвана сильным влиянием вязкости среды на различные аспекты процесса движения. В силу этого в допустимых случаях прибегают к решению уравнений Эйлера для движения идеальных сред с введением необходимых поправок и уточнений. Таким образом, получено одно из важнейших уравнений гидро- и аэродинамики — уравнение (закон) Бернулли.
Уравнение Бернулли.
В практических условиях распространенным является движение в трубах и каналах, когда газ через боковые стенки не расходуется. В таких случаях для расчетов применяется уравнение Бернулли, полученное для струйки тока (трубка тока), характерной тем, что расход газа в любом ее сечении остается неизменным (обмен газом между всем потоком и струйкой тока через ее боковые границы отсутствует).
Для несжимаемого газа ( ) уравнение Бернулли при условии, что все его члены отнесены к единице объема, имеет вид
) уравнение Бернулли при условии, что все его члены отнесены к единице объема, имеет вид
 (10)
(10)
В соответствии с этим величина  является пьезометрическим давлением, величина
является пьезометрическим давлением, величина  — геометрическим давлением, величина
— геометрическим давлением, величина 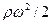 — скоростным давлением.
— скоростным давлением.
Уравнение Бернулли представляет собой закон сохранения энергии, поскольку сумма  характеризует потенциальную, а величина
характеризует потенциальную, а величина 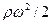 — кинетическую энергию.
— кинетическую энергию.
В металлургической теплотехнике в большинстве случаев пользуются давлением, избыточным над атмосферным. Необходимо уравнение Бернулли привести к такому виду, при котором все члены его были бы выражены в избыточных давлениях. Для этого представим себе канал, окруженный воздухом плотностью  , по которому движется газ плотностью
, по которому движется газ плотностью 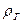 . Принимая плотности газа и воздуха неизменными, напишем уравнение Бернулли и для газа и воздуха применительно к сечениям канала
. Принимая плотности газа и воздуха неизменными, напишем уравнение Бернулли и для газа и воздуха применительно к сечениям канала  и
и  .
.
Уравнение для газа
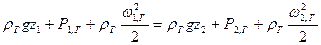 .
.
Уравнение для воздуха (считаем, что воздух находится в спокойном состоянии)
 .
.
Вычитая из первого второе, получаем уравнение Бернулли для газа в избыточных давлениях:
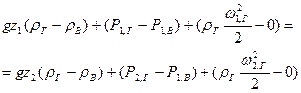 . (11)
. (11)
Уравнение можно переписать в таком виде:
 .
.
Однако равенство 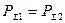 строго справедливо лишь для идеальной среды, полностью лишенной вязкости. Если по каналу перемещается реальная (вязкая) жидкость (газ), то часть энергии тратится на преодоление трения и различных сопротивлений и происходит потеря энергии.
строго справедливо лишь для идеальной среды, полностью лишенной вязкости. Если по каналу перемещается реальная (вязкая) жидкость (газ), то часть энергии тратится на преодоление трения и различных сопротивлений и происходит потеря энергии.
В этом случае при движении от сечення  к сечению
к сечению 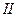
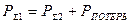 (12)
(12)
и окончательно закон Бернулли формулируется следующим образом: «При установившемся течении несжимаемой жидкости (газа) для различных сечений канала сумма давлений всех видов является постоянной».
Рассмотрим, что представляет собой потерянное давление, входящее в уравнение Бернулли.
При движении реального газа часть его энергии расходуется на преодоление трения и различных сопротивлений.
Потери на местные сопротивления возникают при резком изменении величины и направления скорости, при резком изменении сечения канала, при повороте канала или усложнении его сечения, при соударении потоков. Величину потерь энергии выражают в долях скоростного давления.
Потери на трение  , (Па) можно определить по формуле
, (Па) можно определить по формуле
 (13)
(13)
где  — коэффициент трения;
— коэффициент трения;  — длина канала, м;
— длина канала, м; 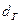 — гидравлический диаметр канала, м;
— гидравлический диаметр канала, м;  и
и  — плотность и скорость жидкости (газа) при нормальных условиях, т.е. при атмосферном давлении и температуре То, равной 273 К; Т — действительная температура жидкости или газа, К.
— плотность и скорость жидкости (газа) при нормальных условиях, т.е. при атмосферном давлении и температуре То, равной 273 К; Т — действительная температура жидкости или газа, К.
При ламинарном движении (Rе<2300) коэффициент трения зависит от критерия Rе
 . (14)
. (14)
При турбулентном движении коэффициент трения зависит не только от критерия Re, но и от относительной шероховатости стенки канала ( 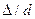 ), равной отношению абсолютной шероховатости
), равной отношению абсолютной шероховатости  (в мм) к диаметру канала
(в мм) к диаметру канала  :
:
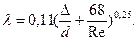
При приближенных практических расчетах коэффициент трения  можно принимать постоянным и равным для кирпичных каналов 0,05, для металлических 0,04.
можно принимать постоянным и равным для кирпичных каналов 0,05, для металлических 0,04.
Потери на преодоление местных сопротивлений (Па), определяются по формуле
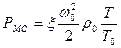 ,
,
где 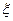 — коэффициент местного сопротивления. Его величина зависит от формы местного сопротивления, как правило, определена опытным путем и приведена в справочной литературе.
— коэффициент местного сопротивления. Его величина зависит от формы местного сопротивления, как правило, определена опытным путем и приведена в справочной литературе.
Важнейшим расчетом, который выполняется для подавляющего большинства печей, является определение суммарных потерь давления на пути движения дымовых газов от печи до дымовой трубы. Суммарные потери используются при определении размеров дымовой трубы, которая рассчитывается из условия, что разрежение, создаваемое дымовой трубой, должно быть по абсолютной величине больше суммы всех сопротивлений, возникающих в дымовом тракте печи.
Таким образом, уравнение (закон) Бернулли находит очень широкое применение. Наряду с уравнением Бернулли важную роль в гидро- и аэродинамике играют также уравнение сплошности (или неразрывности течения) и уравнение импульсов Эйлера.
Уравнение сплошности.
В практических условиях наиболее распространенными являются такие процессы, при которых масса газа, протекающая по какому-то объему, остается неизменной. При этом, естественно, масса газа, втекающая в объем в единицу времени, должна быть равна массе вытекающего газа.
Следовательно, можно написать, что  , или, учитывая, что масса есть произведение скорости, сечения потока и плотности, получаем
, или, учитывая, что масса есть произведение скорости, сечения потока и плотности, получаем
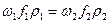 .
.
При условии постоянства плотности ( ) последнее выражение принимает вид
) последнее выражение принимает вид
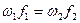 . (15)
. (15)
Если в качестве скорости принимать среднюю скорость потока, то выражение (15) применимо для практических расчетов при течении в трубах и каналах, причем средняя скорость потока определяется как частное от деления секундного объема среды, проходящего через данное сечение, на величину площади сечения, т. е.
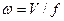 .
.
Уравнение импульсов Эйлера.
Уравнение импульсов (количества движения) Эйлера имеет важное значение для некоторых практических расчетов. Это уравнение применимо к какому-то воображаемому контуру, выделенному в общем потоке газа, через боковую поверхность которого ни движения, ни массообмена не происходит.
В подобном контуре под действием внешних сил (в потоке газа - под действием давления) происходит изменение количества движения газа. Если изменение импульсов проходящего газа и изменение внешних сил отнести к единице времени, то теорема импульсов Эйлера может быть сформулирована следующим образом: «Изменение импульса всех сил, приложенных к газу, проходящему через выделенный контур, равно результирующей внешних сил, действующих на данный контур».
Записывается это уравнение так:
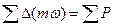 . (16)
. (16)
Применение уравнения импульсов будет проиллюстрировано ниже при рассмотрении струйных аппаратов.
Наиболее важные случаи применения уравнения Бернулли.
Истечение газов через отверстия и насадки
Истечение газов через отверстия и насадки наблюдается при работе горелок, форсунок, при выбивании газа через отверстия в стенах печи и в других случаях. Установим связь между количеством вытекающего газа и размерами отверстия и давлением, под которым происходит истечение. Для простоты возьмем истечение несжимаемого газа, температура которого в процессе истечения практически не изменяется.
Отверстия с острыми краями.
Предположим, что из сосуда очень больших размеров, давление в котором 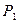 , газ вытекает через отверстие сечением
, газ вытекает через отверстие сечением  в среду с давлением
в среду с давлением  . Для определения скорости истечения газа
. Для определения скорости истечения газа  напишем уравнение Бернулли для сечений
напишем уравнение Бернулли для сечений 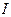 и
и 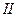 (рис. 8). Поскольку температура газа неизменна, то
(рис. 8). Поскольку температура газа неизменна, то 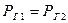 . В этом случае, пренебрегая потерями, можно написать
. В этом случае, пренебрегая потерями, можно написать
 .
.
Вследствие большого размера сосуда можно принять 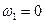 .
.
Тогда
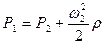 .
.
Отсюда
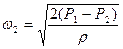 .м/с. (17)
.м/с. (17)
В силу инерции частичек истекающего газа сечение струи  меньше сечения отверстия
меньше сечения отверстия  . Отношение
. Отношение  называется коэффициентом сжатия струи. Скорость
называется коэффициентом сжатия струи. Скорость  фактически относится не ко всему сечению отверстия
фактически относится не ко всему сечению отверстия  , а лишь к сечению струи
, а лишь к сечению струи  . Для определения расхода газа через отверстие
. Для определения расхода газа через отверстие  найдем
найдем  . Но
. Но 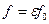 , следовательно,
, следовательно,
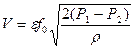 . (18)
. (18)
С учетом гидродинамических потерь при истечении через отверстие выражение (18) принимает вид (м3/с)
 |
 .
.
Смысл коэффициентов  и
и  ясен из следующего примера.
ясен из следующего примера.
Истечение из отверстия в стенке печи (рис. 9) – весьма распространенный на практике случай. Рассмотрим подобный случай истечения (с учетом потерь) из отверстия сечением  , расположенного на участке H от уровня пода печи. Напишем уравнение Бернулли для сечения
, расположенного на участке H от уровня пода печи. Напишем уравнение Бернулли для сечения  и точки A в сечении
и точки A в сечении 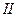 :
:
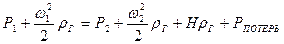 .
.
Скорость движения газов в отверстии  много больше скорости
много больше скорости 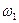 ; исходя из
; исходя из  , принимаем
, принимаем 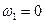 .
.
Как следует из изложенного выше, потери на местные сопротивления могут быть определены как 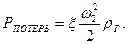
Так как печь сообщается с атмосферой на уровне пода, то пьезометрическое давление газа внутри печи и давление воздуха снаружи равны между собой и равны 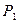 .
.
Давление  в точке А соответствует атмосферному давлению на высоте Н от уровня сечения
в точке А соответствует атмосферному давлению на высоте Н от уровня сечения  , т.е.
, т.е.
 и
и  .
.
С использованием этих зависимостей уравнение Бернулли принимает вид
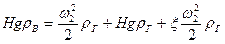
или
 .
.
Отсюда:
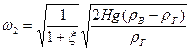 . (19)
. (19)
Величина  учитывает гидравлическое сопротивление отверстия, через которое происходит истечение. Количество истекающей из рассматриваемого течения среды (м3/с)
учитывает гидравлическое сопротивление отверстия, через которое происходит истечение. Количество истекающей из рассматриваемого течения среды (м3/с) 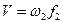 , где
, где 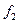 - сечение струи, м2.
- сечение струи, м2.
Но если использовать понятие коэффициента сжатия струи  , то
, то  .
.
Произведение  называют коэффициентом расхода.
называют коэффициентом расхода.
Истечение через насадки.
Насадкой называют короткий патрубок, присоединенный к отверстию в тонкой стенке. Длина насадки обычно составляет 3 – 4 его диаметров. Количество газа, протекающее через насадку, при прочих равных условиях зависит от формы входных кромок и формы самой насадки. Рассмотрим насадки трех видов, представленные на рис. 10. Пользуясь уравнением (19) получим для них


следующие расчетные формулы:
для насадки с острыми кромками:
 ;
; 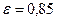 (20)
(20)
 . (21)
. (21)
Для насадок с закругленными кромками и диффузора:
 . (22)
. (22)
Для этих насадок в сечении 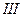 сечения струи и отверстия равны друг другу и поэтому здесь
сечения струи и отверстия равны друг другу и поэтому здесь 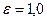 . Сравнение выражений (20), (21) и (22) показывает, что наибольший расход при одинаковом значении
. Сравнение выражений (20), (21) и (22) показывает, что наибольший расход при одинаковом значении  и при одинаковом минимальном сечении насадок получается при истечения газа через диффузор, так как площадь выходного сечения у диффузора
и при одинаковом минимальном сечении насадок получается при истечения газа через диффузор, так как площадь выходного сечения у диффузора  больше, чем у насадок других типов. Угол конусности диффузора не должен превышать 6 – 7º во избежание отрыва потока от стенок диффузора.
больше, чем у насадок других типов. Угол конусности диффузора не должен превышать 6 – 7º во избежание отрыва потока от стенок диффузора.
 Дымовая труба.
Дымовая труба.
Дымовая труба служит для удаления продуктов сгорания из печи. Необходимое разрежение создается в дымовой трубе благодаря стремлению горячих газов подняться, обусловленному разностью плотностей холодного наружного воздуха и горячих газов.
Найдем зависимость разряжения, создаваемого трубой, от высоты трубы H и температуры газов. На рис. 11 представлена схема дымовой трубы. За уровень отсчета принимаем сечение 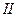 . Напишем уравнение Бернулли в избыточных давлениях для сечений
. Напишем уравнение Бернулли в избыточных давлениях для сечений  и
и 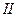 :
:
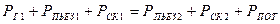 .
.
Труба в сечении 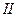 сообщается с атмосферой, поэтому
сообщается с атмосферой, поэтому 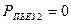 . Из приведенного выше уравнения следует, что пьезометрическое давление в основании трубы
. Из приведенного выше уравнения следует, что пьезометрическое давление в основании трубы
 .
.
Ввиду незначительных скоростей движения газов в трубе величины потерь, выражаемые в правой части приведенного выше уравнения тремя последними членами, значительно меньше абсолютной величины потери, выражаемой первым членом. Следовательно, пьезометрическое давление в основании трубы будет отрицательным, т.е. там будет разряжение. Умножив правую и левую части последовательно на минус единицу, получаем
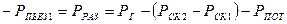 .(23)
.(23)
Потери давления в трубе 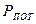 складываются из потерь на трение
складываются из потерь на трение  и потерь, возникающих при выводе газов из трубы в атмосферу и равных
и потерь, возникающих при выводе газов из трубы в атмосферу и равных 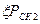 . Учитывая, что коэффициент местного сопротивления на выходе из трубы равен единице (
. Учитывая, что коэффициент местного сопротивления на выходе из трубы равен единице (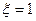 ), можно написать, что
), можно написать, что
 .
.
Вследствие этого уравнение (23):
 . (24)
. (24)
Для того чтобы получить окончательное выражение для  , в уравнение (24) необходимо подставить все входящие в него величины. Температура газов по высоте дымовой трубы и её сечение существенно изменяются, поэтому принимаемые в расчете плотность и скорость движения газов в дымовой трубе определяются по средней температуре по высоте трубы. Величина геометрического давления
, в уравнение (24) необходимо подставить все входящие в него величины. Температура газов по высоте дымовой трубы и её сечение существенно изменяются, поэтому принимаемые в расчете плотность и скорость движения газов в дымовой трубе определяются по средней температуре по высоте трубы. Величина геометрического давления  , входящего в уравнение (24), выражается уравнением (3). Динамические давления будут соответственно равны
, входящего в уравнение (24), выражается уравнением (3). Динамические давления будут соответственно равны
 и
и  .
.
Потери давления на трение находят по уравнению
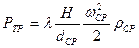 .
.
Подставив в уравнение (24) значения  ,
, 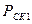 ,
, 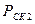 ,
,  и выразив их через скорости и плотности при нормальных условиях (
и выразив их через скорости и плотности при нормальных условиях ( и
и 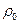 ) по указанным выше выражениям, окончательно получаем (Па)
) по указанным выше выражениям, окончательно получаем (Па)
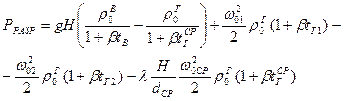 , (25)
, (25)
где  - действительное разрежение трубы в основании дымовой трубы (сечение
- действительное разрежение трубы в основании дымовой трубы (сечение  ), Па;
), Па;  и
и  - плотность соответственно воздуха и газов при нормальных условиях, кг/м3;
- плотность соответственно воздуха и газов при нормальных условиях, кг/м3;  - средний по высоте диаметр трубы, м;
- средний по высоте диаметр трубы, м;  и
и 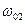 - скорость газов в сечениях
- скорость газов в сечениях  (в основании трубы) и
(в основании трубы) и 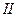 (в устье трубы) при 0ºС, м/с;
(в устье трубы) при 0ºС, м/с; 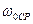 - средняя скорость газов по высоте трубы при 0ºС, м/с;
- средняя скорость газов по высоте трубы при 0ºС, м/с;  - температура окружающего воздуха, ºС;
- температура окружающего воздуха, ºС; 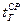 - средняя температура газов по высоте трубы, ºС;
- средняя температура газов по высоте трубы, ºС;  и
и  - температура газов в сечениях
- температура газов в сечениях  и
и 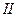 , ºС.
, ºС.
Если учесть, что
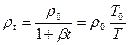 ,
,
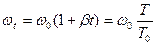 , где
, где  , то выражение (25) может быть переписано следующим образом:
, то выражение (25) может быть переписано следующим образом:
 .
.
Отсюда
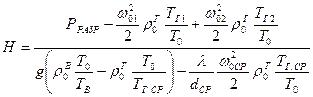 м. (26)
м. (26)
В расчетах разряжение в основании дымовой трубы принимают обычно с запасом, равным  . Величина
. Величина 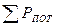 представляет собой суммарные потери давления на пути движения газов от печи до основания дымовой трубы..
представляет собой суммарные потери давления на пути движения газов от печи до основания дымовой трубы..
При расчете дымовой трубы внутренний диаметр в устье ее 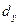 (на выходе) принимают, исходя из скорости газов, равной 3 – 10 м/с (при скорости выхода газов, меньшей 3 м/с, при ветре может происходить их задувание в трубу). Кирпичные и железобетонные дымовые трубы для большей устойчивости делают более широкими в основании. При расчетах внутренний диаметр в основании трубы
(на выходе) принимают, исходя из скорости газов, равной 3 – 10 м/с (при скорости выхода газов, меньшей 3 м/с, при ветре может происходить их задувание в трубу). Кирпичные и железобетонные дымовые трубы для большей устойчивости делают более широкими в основании. При расчетах внутренний диаметр в основании трубы 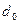 принимают в 1,5 раза больше внутреннего диаметра устья трубы
принимают в 1,5 раза больше внутреннего диаметра устья трубы 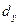 , т.е.
, т.е.  .
.
По условиям выполнения кладки 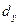 для кирпичных труб не должен быть меньше 0,8 м.
для кирпичных труб не должен быть меньше 0,8 м.
Падение температуры газов на 1 м высоты трубы принимается для кирпичных и железобетонных 1,0 – 1,5ºС, а для металлических 3 – 4 ºС. Ориентировочно высота трубы может быть определена по уравнению (26) без трёх последних его членов. Подсчитав сумму потерь всех видов на пути движения газов от печи до основания дымовой трубы, по уравнению (26) находят расчетную высоту трубы 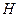 . Независимо от расчета высота дымовой трубы по санитарным нормам должна быть не менее 16 м и в 2 раза выше самого высокого здания, находящегося в радиусе 100 м вокруг трубы.
. Независимо от расчета высота дымовой трубы по санитарным нормам должна быть не менее 16 м и в 2 раза выше самого высокого здания, находящегося в радиусе 100 м вокруг трубы.
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 2166; Нарушение авторских прав?; Мы поможем в написании вашей работы!