Коэффициент теплопроводности

Коэффициент пропорциональности l в уравнении (1.6) на­зывается коэффициентом теплопроводности. Он является физи­ческим параметром вещества и характеризует его способность проводить теплоту.

Размерность .

Значения l для различных веществ определяются опытным путем и для большинства веществ зависят от температуры. Для инженерных расчетов значения l берутся из таблиц физических свойств

Металлы: = 3 ¸ 458 Вт/(м×град). Теплоту в металлах пере­носят свободные электроны.

Диэлектрики (теплоизоляционные, огнеупорные и строительные материалы): = 0,02 ¸ 3,0 Вт/(м×град).

Капельные жидкости: = 0,08 до 0,65 Вт/(м×град).

Газы: = 0,005 ¸ 0,6 Вт /(м×град). Перенос теплоты определяется переносом кинетической энергии в результате хаотического движения и столкновения молекул.

Дифференциальное уравнение теплопроводности

Для определения количества переданной теплоты необходимо знать коэффициент теплопроводности материала и значение тем­пературного градиента, т.е. тем­пературное поле. Для описания температурного поля используют дифференциальное уравнение теплопроводности Фурье, которое имеет вид

(1.7)

Наибо­лее простое соотношение получается, если , т.е. когда внутренние источники теплоты отсутствуют.

В цилиндрических координатах уравнение (1.7) записыва­ется следующим образом:

(1.8)

где r - радиус-вектор; - полярный угол; z - аппликата.

Коэффициент пропорциональности а (м²/с) есть физический параметр вещества, он называется коэффициентом температуропроводности

(1.9)

где c – удельная массовая теплоемкость, Дж/кг К;

r - плотность, кг/м³.

Коэффициент температуропроводности существенен для нестационарных тепловых процессов и характеризует скорость изменения температуры, т.е. является мерой теплоинерционных свойств тела. При этом, чем больше a, тем быстрее меняется во време­ни температура.

Для обозначения суммы вторых производных по координатам используют символ , называемый оператором Лапласа.

Для стационарного температурного поля изменение температуры от времени не происходит и при дифференциальное уравнение теплопроводности упрощается:

Условия однозначности решения

Дифференциальное уравнение Фурье описывает явление передачи теплоты теплопроводностью в самом общем ви­де. Чтобы применить его к конкретному случаю, необходимо задать условия однозначности, или краевые условия:

1. геометрическую форму и размеры тела;

2. физи­ческие параметры среды и тела;

3. начальные условия (распределение температуры в теле в начальный момент времени);

4. граничные условия, характеризующие взаимодействие тела с окружающей средой.

Начальные условия необходимы при рассмотрении нестационарных процессов и состоят в задании закона распределе­ния температуры внутри тела в начальный момент времени. В общем случае начальное условие аналитически может быть запи­сано следующим образом:

при (1.10)

Граничные условия могут быть заданы несколькими спосо­бами.

А. Граничные условия 1-го рода.

Задается распределение температуры на поверхности те­ла для каждого момента времени:

(1.11)

где t_с - температура на поверхности тела; х, у, z - координаты поверхности тела.

В частном случае: .

Б. Граничные условия 2-го рода

Задаются величины плотности теплового потока для каж­дой точки поверхности тела и любого момента времени.

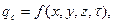(1.12)

где q_П - плотность теплового потока на поверхности тела.

В простейшем случае

В. Граничные условия 3-го рода

Задается температура окружающей среды t_ж и закон теп­лообмена между поверхностью тела к окружающей средой. Для этого чаще всего используется закон Ньютона – Рихмана, согласно которому ко­личество теплоты, отводимое через единицу поверхности тела в едини­цу времени, пропорционально разности температур поверхности тела t_с и окружающей среды t_ж

, (1.13)

где - коэффициент пропорциональности, называемый коэффи­циентом теплоотдачи, Вт/(м²×град); он характеризует интенсивность теплообмена между поверхностью тела и окружающей средой.

Согласно закону сохранения энергии количество теплоты, ко­торое отводится с единицы поверхности в единицу времени вследствие теплоотдачи (1.13), должно равняться теплоте, подводимой к единице поверхности в единицу времени вследствие тепло­проводности из внутренних объемов тела (1.6), т.е.

где n - нормаль к поверхности тела.

Окончательно граничные условия 3-го рода можно записать в виде:

(1.14)

Дата добавления: 2014-01-04