Векторное изображение синусоидально изменяющихся величин. Векторные диаграммы

До сих пор мы с вами синусоидальные величины изображали графически или записывали их формулы. Есть еще один способ отображения синусоиды – вращающийся вектор.

Пусть переменный ток задан уравнением

i = I_m sin (ωt + ψ) (5.12)

Проведем две взаимно-перпендикулярные оси и из точки пересечения осей построим вектор. Длину этого вектора, в определенном масштабе, приравняем амплитуде I_{m .} Направление вектора пусть определяется начальной фазой рассматриваемого тока ψ. Рядом нарисуем декартовые оси координат i = f(ωt). Спроецируем наш вектор на ось i. Проекция будет равна

i₀ = I_m sin ψ (5.13)

Теперь начнем вращать вектор против часовой стрелки с угловой частотой ω. Тогда положение вектора в любой момент времени будет определяться углом

ωt + ψ.

Для времени t₁ проекция вектора на ось i будет равна:

i₁ = I_m sin (ωt₁ + ψ) (5.14)

Для времени t_n:

i_n = I_m sin (ωt_n + ψ) (5.15)

и так далее.

В общем случае:

i = I_m sin (ωt + ψ) (5.16)

Таким образом, формула, описывающая проекцию вращающегося вектора длиной I_m такая же, что и формула мгновенного значения тока. Это и позволяет нам изображать переменные синусоидальные величины в виде вращающихся векторов.

Это подтверждается и тем, что вращая наш вектор против часовой стрелки можно построить график изменения указанной проекции во времени. Получим синусоиду в пределах одного оборота, см. рис. 5.3

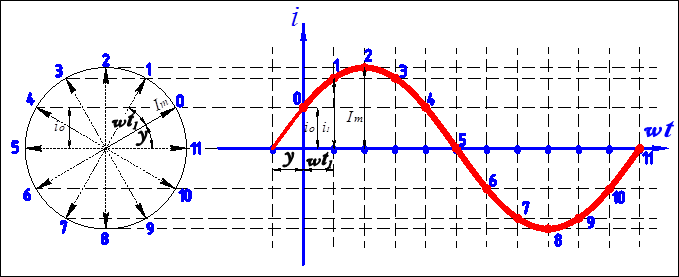
Рис. 5.3 Построение синусоиды с помощью вращающегося вектора

При построении векторов положительным направлением считается движение против часовой стрелки.

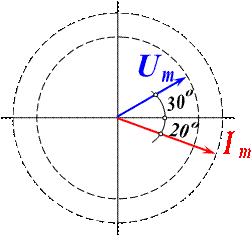Если на одном чертеже изобразить несколько векторных величин одной частоты – получим векторную диаграмму. Например, напряжение и ток конкретной электрической цепи выражаются уравнениями:

u = 125 sin (ωt + 30⁰) (5.17)

i = 12 sin (ωt -20⁰) (5.18)

Рис. 5.4 Векторная диаграмма

Если выбрать масштабы напряжения и тока М_U = 50 В/см; М_I = 4 А/см, получим длину вектора напряжения 2,5 см; вектора тока 3 см – смотри рис. 5.4.

На векторной диаграмме изображают переменные величины одной частоты, поэтому их взаимное расположение не меняется. Начало отсчета времени выбирается произвольно. Поэтому один из векторов чертится произвольно, остальные – с учетом сдвига фаз.

Векторные диаграммы очень удобны для сложения и вычитания синусоидальных величин. Требуется, например сложить два тока:

i₁ = I₁ sin (ωt + ψ₁); i₂ = I₂ sin (ωt + ψ₂) (5.19)

Сумма токов:

i = I₁ sin (ωt + ψ₁) + I₂ sin (ωt + ψ₂) (5.20)

– громоздко и ненаглядно.

Можно начертить синусоиды токов в одной системе координат и для ряда аргументов найти сумму токов. Если соединить полученные значения, получится синусоида. Этот способ тоже неудобен.

Гораздо проще складывать и вычитать вектора на векторных диаграммах. Для этого нужно знать правила сложения векторов. Вы их прекрасно знаете из школьной программы.

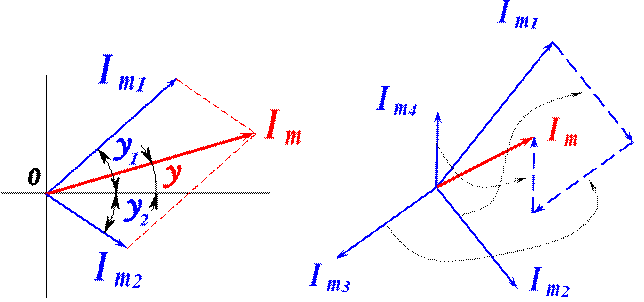
Рис 5.5 Сложение векторов

Дата добавления: 2014-01-04