Цепь с емкостью

В конденсаторе с идеальным диэлектриком предполагается полное отсутствие тока проводимости и потерь энергии. Пусть напряжение на емкости u=U_msinwt. Определим ток и мощность.

Изменение напряжения между обкладками сопровождается электрическим током поляризации, величина которой зависит от емкости С.

Когда мы изучали конденсаторы, было установлено, что электрическое поле вызывает поляризацию диэлектрика, размещенного между обкладками конденсатора. Если электрическое поле меняется, изменяется и поляризованность диэлектрика. При этом связанные заряженные частицы, в обкладках конденсатора, перемещаются, а перемещение зарядов – это электрический ток.

Явление движения связанных заряженных частиц в обкладках конденсатора при изменении поляризации диэлектрика называют электрическим током поляризации.

Наличие электрического тока поляризации позволяет рассматривать цепь с конденсатором непрерывной – в проводниках, присоединенных к обкладкам конденсатора течет обычный ток равный току поляризации.

Заряд конденсатора пропорционален напряжению между обкладками, поэтому изменение мгновенного значения напряжения сопровождается изменением заряда конденсатора.

dq = Cdu (6.20)

При этом скорость изменения заряда пропорциональна скорости изменения напряжения

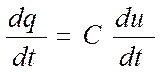(6.21)

Но скорость изменения заряда и есть электрический ток. После дифференцирования:

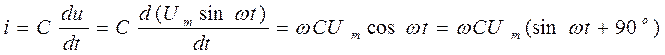
(6.22)

Это же уравнение можно было получить, построив векторную диаграмму, аналогичную той, которую мы строили для цепи с индуктивностью.

Из последнего уравнения видно, что в цепи с емкостью ток опережает напряжение, а напряжение отстает от тока на 90^о или на p/2.

Выражение wСU_m = I_m – есть амплитуда тока.

Разделим это выражение на Ö2 и получим:

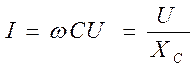(6.23)

Величину 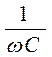обозначают Х_С и называют реактивным сопротивлением емкости или емкостным сопротивлением.

Последняя формула похожа на закон Ома. Емкостное сопротивление – это противодействие заряженного конденсатора току цепи.

Разберемся с мощностью. График мгновенной мощности (рис 6.8) строится так же, как и график для цепи с индуктивностью.

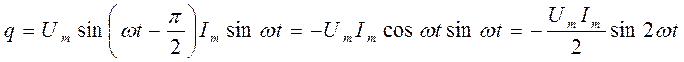
(6.24)

Из графика видно, что так же, как и в цепи с индуктивностью, мощность 4 раза за период меняет знак. Во вторую и четвертую четверти энергия (мощность) накапливается в электрическом поле конденсатора, а в первую и третью четверти то же количество энергии возвращается к источнику (конденсатор разряжается).

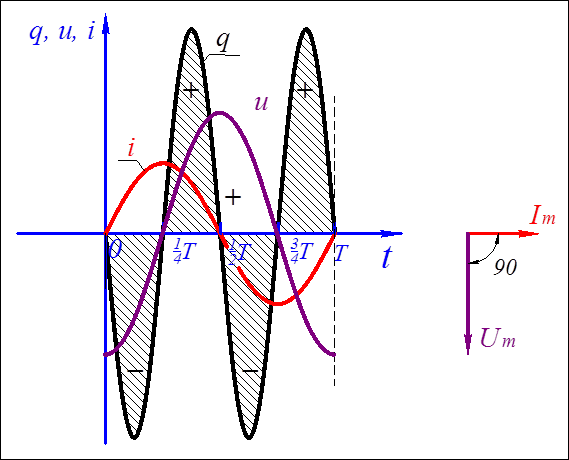
Рис. 6.8 Мощность в цепи с емкостью

Т.о. в цепи с емкостью имеет место колебание мощности между источником и электрическим полем конденсатора. Она так же, как и в цепи с индуктивностью называется реактивной. Емкостное сопротивление – реактивное сопротивление.

В цепи с емкостью преобразования электрической энергии в другие виды энергии не происходит.

Реактивная мощность в цепи с емкостью:

Q = UI = U²wC (6.25)

Реактивная мощность в цепи с емкостью колеблется в противофазе с реактивной мощностью цепи с индуктивностью.

6.4 Последовательное соединение R, L, С

До сих пор мы рассматривали идеальные индуктивности и емкости. Однако, каждый из этих элементов имеет и активную составляющую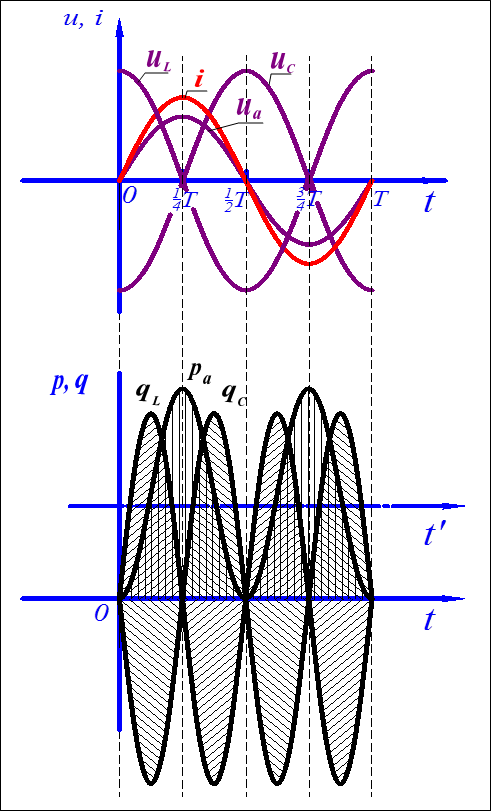

6.10 Графики основных величин при последовательном соединении R,L,C

сопротивления. Кроме того, активные сопротивления имеют проводники, по которым подводится напряжение к указанным элементам. Поэтому в реальных цепях всегда присутствуют и активные и реактивные сопротивления – см. рисунок.

При прохождении переменного тока i=I_msinwt через электриче­скую цепь, состоящую из последо­вательно соединенных элементов R, L, С на зажимах этой цепи создается переменное на­пряжение, равное алгебраической сумме переменных напряжений на отдельных элементах (второй закон Кирхгофа):

и = u_R+и_L+ и_C (6.26)

Напряжение u_R на сопротивле­нии R совпадает по фазе с током i, напряжение u_L на индуктивности L опережает, а напряжение и_C на ем­кости С отстает от i на p/2. Следовательно, напря­жение и на зажимах всей цепи равно:

u=U_m sin (wt + j) = RI_m sin wt + wLI_m sin (wt + ) +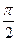

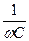+ I_m sin (wt - 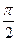) = RI_m sin wt + (wL - 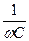) I_m sin (wt + )

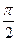(6.27)

Это уравнение представляет собой тригонометрическую форму записи второго закона Кирхгофа для мгно­венных значений напряжений. Вхо­дящая в него величина

x = x_L- x _C = wL - 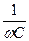(6.28)

называется реактивным сопротивлением цепи, которое в зависимости от знака мо­жет иметь индуктивный (X>0) или емкостный (Х<0) характер. В отли­чие от реактивного сопротивления Х, активное сопротивление R всегда по­ложительно.

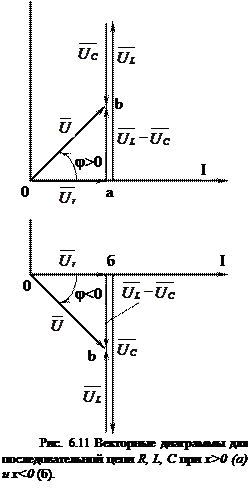
Построим векторные диаграммы для случаев, когда X>0 и Х<0.

Падение напряжения от тока в активном и реактивном сопротив­лениях изображается катетами пря­моугольного треугольника напряже­ния 0аb, гипотенуза которого изо­бражает напряжение на зажимах цепи. Отсюда

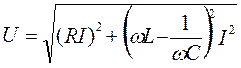(6.29)

или 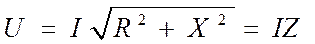(6.30)

Полученное выражение показы­вает, что действующие значения (так же, как и амплитуды) напря­жения на зажимах цепи и тока, про­ходящего через данную цепь, свя­заны соотношением, аналогичным закону Ома.

Выражение

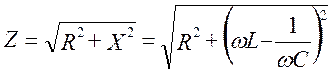(6.31)

называется полным сопротивлением рассматриваемой цепи.

Поскольку последние два уравнения (для напряжения и для полного сопротивления) похожи на теорему Пифагора, можно ввести понятия треугольника напряжений и треугольника сопротивлений. Треугольники напряжений видны на векторных диаграммах. Треугольники сопротивлений, очевидно, будут выглядеть так:

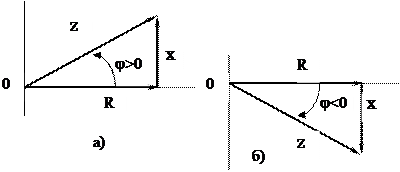Рис.6.12 Треугольники сопротивлений

Активное, реактивное и полное сопротивления относятся к числу основных понятий, применяемых в теории электрических цепей. Из векторных диаграмм следует:

Угол j положителен при индуктивном характере цепи, т. е. при Х>0; при этом ток отстает по фазе от напряжения.

Угол j отрицателен при емкост­ном характере цепи, т. е. при Х<0, при этом ток опережает по фазе на­пряжение.

Ток совпадает с напряжением по фазе при Х =Х _L- X_C= 0, т. е. при равенстве индуктивного и емкост­ного сопротивлений. Такой режим работы электрической цепи назы­вается резонансом напря­жений.

Из треугольника сопротивлений следует, что активное и реактивное сопротивления цепи связаны с пол­ным сопротивлением формулами:

R = Z cos j; X = Z sin j (6.32)

Умножив правые и левые части этих выражений на действующее значение тока I, получим действующие значения на­пряжений на активном и ре­активном сопротивлениях, изображаемые катетами тре­угольника напряжений и на­зываемые активной и ре­активной составляю­щими напряжения:

U_a= RI = ZIcosj = Ucosj (6.33)

U _p= XI = ZIsinj = Usinj (6.34)

Мгновенные значения напряже­ний на активном и реактивном со­противлениях, суммирующиеся ал­гебраически имеют фазовые сдвиги ± p/2. Поэтому непосредственное сложение дейст­вующих значений этих функций не дает действующего значения на­пряжения на всей цепи. Как видно из треугольника напряжений, активная и ре­активная составляющие напряже­ния связаны с действующим значе­нием суммарного напряжения фор­мулой

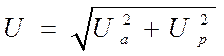(6.35)

Если все стороны треугольника напряжений разделить на I, то по­лучится прямоугольный тре­угольник сопротивлений, подобный треугольнику напряже­ний.

Умножим в последнем выражении обе части на действующее значение тока

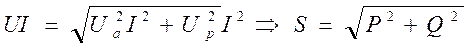(6.36)

Получилось уравнение полной мощности S (P – активная мощность, Q – реактивная мощность). Уравнение хорошо интерпретируется треугольником мощностей.

Рис.6.13 Треугольники мощностей

Само собой: P = S cos j = UI cos j - формула активной мощности в сетях переменного тока.

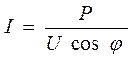(6.37)

Из последней формулы следует важный практический вывод – для того чтобы уменьшить ток в сети переменного тока для передачи заданной активной мощности, а следовательно и потери напряжения на активных сопротивлениях, нужно стремиться уменьшить реактивную мощность. Другими словами – нужно уменьшать угол j, или увеличивать cos j, который называется коэффициентом мощности сети переменного тока.

В сетях переменного тока реактивная мощность появляется, в основном, за счет индуктивностей (трансформаторы, двигатели обладают обмотками). Поэтому, чтобы уменьшить ток в сети, нужно компенсировать реактивную мощность индуктивности.

6.5 Параллельное соединение R, L, С

Рассмотрим схему. Пусть для этой цепи известны напряжение u=U_msinwt и параметры R, L, С.

В схеме активные и реактивные сопротивления заменены соответствующими проводимостями G и В. Требуется найти токи в цепи и мощность.

В соответствии с 1 законом Кирхгофа имеем право записать:

i = i₁+i₂+i₃+i₄+i₅ = i_1a+ i_1p+ i_2a+ i_2p+ i_3a+i_4p+i_{5 p}

Для действующих токов можем записать векторное уравнение.

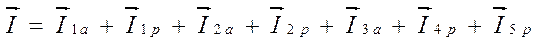
Можем построить и векторную диаграмму (б).

Из векторной диаграммы видно, что все активные составляющие векторов тока направлены одинаково – параллельно вектору напряжения, поэтому векторную сумму можно заменить арифметической суммой:

I_a = I_1a+I_2a+I_3a

Реактивные составляющие векторов тока перпендикулярны вектору напряжения, причем индуктивные токи направлены в одну сторону, емкостные – в другую. Поэтому реактивная составляющая полного тока будет определяться алгебраической суммой, в которой индуктивные токи положительные, а емкостные токи отрицательные:

I_p = -I_1p+I_2p- I_4p+I_5p

Векторы активного, реактивного и полного токов всей цепи образуют прямоуголный треуголник, из которого следует

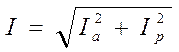
Если токи выразить через напряжение и соответствующие проводимости ветвей, получим:

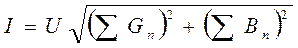
Подкоренное выражение

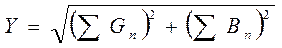
Называется полной проводимостью цепи. Тогда:

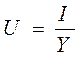
åG_n – общая активная проводимость, равная арифметической сумме активных проводимостей всех ветвей. åB_n – общая реактивная проводимость, равная алгебраической сумме реактивных проводимостей всех ветвей (индуктивные проводимости положительные, емкостные – отрицательные).

Как видим, полная, активная и реактивная проводимости опять связаны теоремой Пифагора.

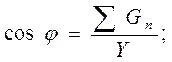
От треугольника проводимостей можно перейти к треугольнику мощностей:

P = UIcosj; Q = UIsinj; S = UI

Активную мощность цепи можно представить как арифметическую сумму мощностей ветвей.

Реактивная мощность цепи равна алгебраической сумме реактивных мощностей ветвей – индуктивная мощность берется положительной, емкостная мощность – отрицательной.

P = åP_n; Q = åQ_n;

Дата добавления: 2014-01-04