Сечения ядерных реакций

Акт ядерной реакции, как и все процессы в микромире, является случайным явлением. Поэтому для количественного описания возможности ядерной реакции необходимо использовать вероятностный подход. Такой количественной характеристикой вероятности протекания реакции является эффективное сечение, которое определяется следующим образом. Пусть на площадку S = 1 см ² тонкой пластинки, содержащей ядра-мишени А, падает перпендикулярно однородный в пределах площадки поток 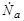- количество частиц а в единицу времени. Тонкой будем считать пластинку, в которой ядра А не перекрывают друг друга. Оценим толщину пластинки. Так как размеры ядер меньше размеров атомов примерно в 10⁴ раз, то соответствующие им площади будут различаться в 10⁸ раз. В твердом теле атомы упакованы плотно, поэтому необходимо 10⁸ слоев атомов для заметного перекрытия ядер друг другом. Принимая диаметр одного атома примерно равным 10^-8 см, получим, что толщина δ пластинки составит ~1 см. В слое dx << δ (отсутствие перекрытия ядер-мишеней) возможное число реакций в 1 см ² пластинки

,

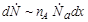(4.3.1)

где n_А – концентрация ядер-мишеней А. Тогда вероятность (доля) реакций составит, согласно (4.3.1)

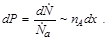
(4.3.2)

Запишем (4.3.2) в виде точного равенства:

,

(4.3.3)

где σ – коэффициент пропорциональности, имеющий размерность площади, называется эффективным (микроскопическим) сечением ядерной реакции. Так как

(4.3.4)

где V – объем пластинки, а N_A – число ядер А в этой пластинке, то выражение (4.3.4) есть ничто иное, как отношение эффективной площади, занятой всеми ядрами пластинки, к площади пластинки. Поэтому эффективное сечение можно представить как среднее значение площади, в которой с определенной вероятностью должна произойти реакция при условии нахождения в ее пределах частиц а и А. В ядерной физике для измерения сечений используется специальная единица, называемая барн (б), 1 б = 10^-24 см ².

Часто используется также понятие макроскопического сечения

S = ns,

(4.3.5)

имеющего размерность длины. Физический смысл этой величины выясним ниже.

Перепишем (4.3.3) в виде

(4.3.6)

и разделим левую и правую части равенства (4.3.6) на бесконечно малый объем dV = Sdx. В результате получим

(4.3.7)

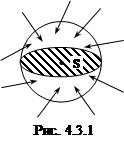В ядерной физике оказалось удобным использовать величину плотности потока частиц Ф. Пусть в объем сферы (рис. 4.3.1) с площадью поперечного сечения S по всевозможным направлениям поступает однородный в пределах объема сферы поток частиц 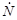. По определению плотность потока есть

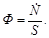
(4.3.8)

Введем величину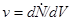- числа реакций, происходящих в бесконечно малом объеме вещества мишени в единицу времени. С учетом этого и (4.3.8) выражение (4.3.7) принимает вид

,

(4.3.9)

где Ф_а – плотность потока частиц а. Выражение (4.3.9) будет нами неоднократно использоваться.

Установим, как изменяется плотность потока при движении частиц а в пластинке. Число реакций в тонком слое мишени толщиной dx в единицу времени равно n dx, а с другой стороны равно убыванию плотности потока частиц в этом слое, то есть

n dx = - dФа.

(4.3.10)

Используя (4.3.9) получаем дифференциальное уравнение для ослабления плотности потока частиц а:

dФа = - s nАФаdx,

(4.3.11)

которое следует интегрировать с граничным условием Ф_а (х = 0) = Ф ₀. Сечение s также является функцией х, но часто (например, в случае прохождения тепловых нейтронов через вещество) можно приближенно считать, что s не зависит от x. Тогда, разделяя переменные в (4.3.11), получим после интегрирования:

=

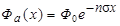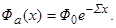
(4.3.12)

Из (4.3.12) получаем вероятность частице а пройти без столкновений путь х:

=

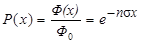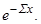
(4.3.13)

Найдем среднюю длину пробега частиц а до вступления в реакцию:

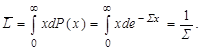
(4.3.14)

В этом случае макроскопическое сечение S [ см^-1 ] имеет смысл среднего числа взаимодействий частиц а на единице длины пути в мишени, то есть смысл коэффициента поглощения вматериале мишени.

Более подробной характеристикой ядерного взаимодействия (реакции или рассеяния) служит дифференциальное сечение:

(4.3.15)

Дифференциальное сечение определяет плотность вероятности продуктам (В или b) реакции (4.1.1) вылететь в пределах телесного угла dω в направлении (рис. 4.3.2). Дифференцируя (4.3.3) по ω, получим выражение:

,

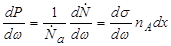(4.3.16)

которое устанавливает связь между дифференциальным сечением и плотностью вероятности. Если спины налетающих частиц и ядер-мишений ориентированы хаотично, то процесс взаимодействия не зависит от полярного угла φ и определяется только азимутальным углом θ вылета одной из частиц. Так как dω = sinθdθdφ, то

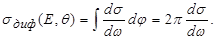
(4.3.17)

Зависимость дифференциального сечения от угла θ называется угловым распределением.

Интегрирование (4.3.17) по углу θ устанавливает связь между эффективным сечением и угловым распределением:

(4.3.18)

Часто вместо зависимости s(E, q) используют зависимость s(Е, m), где m º cosq. Тогда

.

(4.3.19)

На одних и тех же ядрах А под действием частиц а могут иметь место различные выходные каналы (см. (4.1.2), каждый из которых характеризуется своим парциальными микроскопическим σ_i и макроскопическим Σ _i сечениями. Тогда, в соответствие с (4.3.6), сечения входного канала или полные сечения s_t и Σ _t складываются из парциальных сечений следующим образом:

.

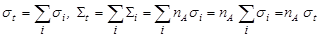(4.3.20)

Если же вещество мишени имеет в своем составе ряд различных нуклидов, концентрация ядер каждого из которых равна n_j, то в этом случае можно говорить только о полном макроскопическом сечении

,

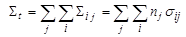(4.3.21)

где 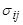- микроскопическое сечение реакции вида i на ядрах j, или о средней (приходящейся на одно ядро) величине микроскопического сечения реакции вида i:

.

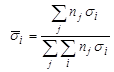(4.3.22)

Используя (4.3.14) и (4.3.20) или (4.3.21) можно рассчитать полную среднюю длину пробега 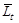частиц а:

,

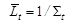(4.3.23)

Вероятность осуществления ядерной реакции, непосредственно измеряемой в физических экспериментах и позволяющий экспериментально определить макроскопическое сечение, является выход ядерной реакции Y или просто выход. Выход определяется как число частиц а, испытавших взаимодействие в единицу времени, отнесенное к полному числу частиц а, падающих на мишень макроскопических размеров в единицу времени. Вид формулы, связывающей выход и макроскопическое сечение, определяется конкретным видом ядерной реакции. Для примера рассмотрим процесс (4.3.12) на мишени толщиной d:

.

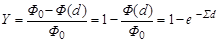(4.3.24)

После небольших преобразований и логарифмирования получаем формулу для нахождения макроскопического сечения

,

(4.3.25)

если, как обычно, Y << 1.

Для экспериментального определения дифференциального сечения необходимо измерить угловое распределение продуктов реакции или рассеяния частиц а

Дата добавления: 2014-01-04