Цепная реакция деления

Возникновение вторичных нейтронов в процессе деления тяжелых ядер нейтронами позволяют осуществить процесс цепной реакции деления. Цепной процесс характерен тем, что в его основе лежит экзоэнергетическая реакция, возбуждаемая нейтроном, которая
порождает вторичные нейтроны. В этом случае появление нейтрона в делящейся среде вызывает цепь следующих друг за другом реакций деления, которая продолжается до обрыва вследствие потери нейтрона – носителя процесса. Основных причин потерь две: поглощение нейтрона ядром без испускания вторичных (например, радиационный захват) или уход нейтрона за пределы объема вещества (называемый активной зоной), в котором протекает цепной процесс деления. Если в результате реакции возникает более одного нейтрона, которые в свою очередь вызывают деление, то такая реакция является разветвленной реакцией. Средняя длина пробега нейтрона от точки рождения до точки, в которой нейтрон производит деление, является макроскопической величиной. Поэтому цепная реакция деления является макроскопическим процессом. Каждый нейтрон, участвующий в цепном процессе, проходит цикл обращения: рождается в реакции деления, некоторое время существует в свободном состоянии, затем либо теряется, либо порождает новый акт деления и дает нейтроны следующего поколения. Нейтрону необходимо, хотя и малое, но конечное время для прохождения через цикл обращения. Среднее время τ, полученное усреднением по большому числу нейтронных циклов деления, называется временем нейтронного цикла или средним временем жизни нейтронов. Таким образом, цепной процесс деления можно представит как последовательность следующих друг за другом лавин или поколений, разделенных промежутком времени τ:

N 0→ N 1→ N 2→ …→ Ni → Ni +1→…,

(5.3.1)

где N –число нейтронов в данном поколении. Отношение числа нейтронов последующего поколения к их числу в предшествующем поколении во всем объеме активной зоны называется коэффициентом размножения нейтронов:

k = Ni +1/ Ni.

(5.3.2)

Величины τ и k полностью определяют развитие цепного процесса во времени. Действительно, число нейтронов в следующем поколении N_{i +1} = k N_i, затем, через промежуток времени τ количество нейтронов N_{i +2} = k N_{i+ 1} = k ² N_i, через время 2 τ количество нейтронов составит N_{i +3} = k N_{i+ 2} = k ² N_{i+ 1} = k ³ N_i и т.д. Количество нейтронов в поколении под номером m (число нейтронных циклов) составит

Nm = N 0 k^m,

(5.3.3)

если число нейтронов в начальный момент времени наблюдения равно N ₀. Время наблюдения при этом составит t = mk, что позволяет записать зависимость (5.3.3) в явном виде от времени:

N (t) = N 0 k^t^/^τ.

(5.3.4)

Однако, выражения (5.3.3) и (5.3.4) верны только приблизительно, поскольку случаи рождения и исчезновения нейтронов происходят случайным образом, и в любой момент времени в активной зоне присутствуют нейтроны из разных поколений, т.е. процесс изменения числа нейтронов в активной зоне происходит непрерывно.

Приращение числа нейтронов в цепном процессе за бесконечно малый промежуток времени dt составит:

dN = Nk – N = N (k – 1),

(5.3.5)

а скорость изменения числа нейтронов будет равна

.

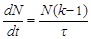(5.3.6)

Уравнение (5.3.6) называется точечным уравнением кинетики без запаздывающих нейтронов. Разделяя в (5.3.6) переменные получаем решение этого уравнения:

,

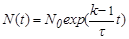(5.3.7)

где N ₀ = N (t = 0) - число нейтронов в начальный момент наблюдения.

Проанализируем выражение (5.3.7).

Если k > 1, то число нейтронов в активной зоне будет непрерывно увеличиваться и процесс цепной реакции, раз возникнув, будет сам собой развиваться во времени. Процесс с k > 1 носит название надкритического режима.

При k = 1 количество нейтронов в активной зоне и число происходящих в единицу времени делений не изменяются со временем и остаются постоянными. Такой режим носит название критического режима.

Наконец, если k < 1, то процесс размножения нейтронов затухает и называется соответственно подкритическим режимом.

Таким образом, для протекания самоподдерживаемой цепной реакции деления необходимо, чтобы k ≥ 1. Для определения возможности осуществления цепной реакции обычно рассматривают коэффициент k _∞ размножения в среде с бесконечным объемом, когда можно пренебречь утечкой нейтронов через поверхность активной зоны. Тогда для активной зоны конечных размеров

k = κ k ∞,

(5.3.8)

где κ – вероятность нейтрону избежать утечки из активной зоны конечного объема. Если существует некоторый конечный объем, то конфигурация, состав и масса активной зоны, при которых выполняется условие

k = κ k ∞ ≥ 1,

(5.3.9)

называются критическими параметрами. Величина k зависит от многих параметров: нуклидного состава активной зоны, ее формы и размера, от энергетического спектра нейтронов, вызывающих деление. Расчет величины k является сложной инженерно-физической задачей и требует знания огромного числа констант, определяющих протекание цепного процесса.

Рассмотрим цепной процесс, у которого время нейтронного цикла τ ≈ 10^-3 с. Такая величина τ характерна для реакторов на тепловых нейтронах. Если предположить, что коэффициент размножения k = 1,005, то за одну секунду число нейтронов, согласно (5.3.7). увеличится в

(5.3.10)

В такое же число раз возрастет количество делений в единицу времени и, следовательно, мощность установки. Ясно, что управлять таким процессом невозможно и в контролируемой установке превышение k над единицей всего на 0,5% недопустимо. Приведенная оценка не учитывает запаздывающих нейтронов и поэтому является завышенной. Действительно, число нейтронов в активной зоне в данный момент времени может быть представлено следующим образом:

Ni+ 1 = Np + Nd,

(5.3.11)

где: N_p – количество мгновенных нейтронов (p – prompt), возникших непосредственно в момент деления ядер; N_d – количество запаздывающих нейтронов (d – delay), возникших из осколков деления в результате запаздывающего энерговыделения. Разделив равенство (5.3.11) слева и справа на количество нейтронов N_i в предыдущем цикле и учитывая определение (5.3.2), получим, что коэффициент размножения может быть представлен в виде суммы двух слагаемых:

k = kp + kd,

(5.3.12)

из которых первое является коэффициентом размножения на мгновенных нейтронах, а второе – коэффициентом размножения на запаздывающих. Вспомним, что доля запаздывающих нейтронов в полном числе вторичных нейтронов деления обозначается β (см. определение (5.2.8) и таблицу (5.2.2.). Тогда в цепном процессе, идущем в ²³⁵U под действием тепловых нейтронов

kp = k (1 – β) = 1,005(1 – 0,0065) = 0,9985,	(5.3.12)
kd = k β =1.005·0,0065=0,0653.	(5.3.12)

Таким образом, цепной процесс на одних только мгновенных нейтрона является подкритическим, и управление процессом осуществляется с помощью изменения количества запаздывающих нейтронов. Если k_p становится равным или больше единицы, что соответствует k ≥ (1 + β), то цепной процесс становится неконтролируемым.

Найдем среднее время τ₀ нейтронного цикла с учетом запаздывающих нейтронов. По правилу нахождения среднего

τ0 = (1 – β)τ p + βτ d,

(5.3.14)

где τ _p – среднее время жизни мгновенных нейтронов, а τ _d – запаздывающих. Например, среднее время жизни запаздывающих нейтронов для ²³⁵U составляет около 13 с и для τ _p ≈ 10^-3 с получаем

τ0 = 10^-3 + 0,085 ≈ 0,085 с.

(5.3.15)

Из приведенного примера следует важный вывод о том, что среднее время нейтронного цикла цепного процесса определяется средним временем жизни запаздывающих нейтронов и не зависит от времени жизни быстрых, но при условии k < (1 + β). Используя в примере (5.3.10) время τ = τ₀ = 0,085 с получим, что за одну секунду мощность цепного процесса увеличится всего на 6 %, что не представляет проблем для регулирования. В теории регулирования цепного процесса обычно используется величина T, называемая периодом реактора, которая есть время, в течение которого количество нейтронов в активной зоне увеличивается в «е» раз. Из (5.3.7) получаем, что

.

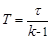(5.3.16)

Если опять же принять k = 1,05, а τ = 0,085 с, то период реактора Т = 17 с. При k → 1 T → ∞, что следует непосредственно из (5.3.16).

Рассмотрим кинетику цепного процесса с учетом запаздывающих нейтронов. Скорость приращения мгновенных нейтронов, по аналогии с (5.3.6), будет равна

,

(5.3.17)

а скорость приращения запаздывающих в соответствии с законом радиоактивного распада осколков относительно испускания запаздывающих нейтронов (λ – постоянная такого распада) равна

,

(5.3.18)

где с – количество накопившихся в предыдущих поколениях ядер предшественников запаздывающих нейтронов. Полная скорость изменения числа нейтронов нейтронов

.

(5.3.19)

Это уравнение необходимо дополнить уравнением для скорости образования ядер предшественников:

.

(5.3.20)

Уравнения (5.3.19) и (5.3.20) образуют систему связанных линейных дифференциальных уравнений точечной кинетики с учетом запаздывающих нейтронов. При более точном рассмотрении учитывают шесть временных групп запаздывающих нейтронов и получают систему из семи уравнений.

Покажем, что на тепловых нейтронах можно организовать цепной процесс деления на уране природного состава: относительное атомное содержание ²³⁸U составляет 99,28 %, ²³⁵U – 0,714 % и ²³⁴U – 0,006 %. Тепловыми нейтронами делятся только нуклиды ²³⁵U и ²³⁴U. Ввиду ничтожного содержания ²³⁴U его участие в цепном процессе учитывать не будем. Среднее число η вторичных нейтронов на один акт поглощения теплового нейтрона ураном природного состава будет равно (дробь определяет вероятность нейтрону произвести деление):

,

(5.3.21)

где: - среднее число вторичных нейтронов на один акт деления; n –концентрация ядер нуклида ²³⁵U или ²³⁸U (с соответствующими верхними индексами); σ _а –сечение захвата нейтронов ядрами ²³⁵U или ²³⁸U; ⁵σ _f – сечение деления ядер ²³⁵U нейтронами. Для тепловых нейтронов эти величины равны: = 2,44; σ _а = 694 барн для ядер ²³⁵U; σ _а = 2,8 барн для ядер ²³⁸U; ⁵σ _f =582 барн для ядер ²³⁵U (рис. 5.2.1). Для природного урана ⁸ n /⁵ n = 99,28/0,714 = 139. Подставив эти значения в формулу (5.3.21), получим η = 1,31. Таким образом, цепной процесс на ядрах ²³⁵U в составе природного урана возможно осуществить, если при замедления вторичных нейтронов деления до тепловых энергий потерять в среднем не более 0,3 нейтрона.

Однако самопроизвольный цепной процесс деления в природном уране произойти не может и вот почему. При делении ядер средняя энергия вторичных нейтронов составляет ~ 2 МэВ. Для нейтронов с такой энергией входящие в формулу (5.3.21) величины равны: = 2,65; σ _а = 2,1 барн для ядер ²³⁵U; σ _а ≈ 0,1 барн для ядер ²³⁸U; ⁵σ _f =2 барн для ядер ²³⁵U (см. рис. 5.2.1). Подставив эти величины в формулу (5.3.21) получим η(²³⁵U) ≈0,33. Теперь необходимо учесть деление быстрыми нейтронами ядер ²³⁸U. Сечение деления ⁸σ _f ядер ²³⁸U при энергии 2 ÷ 6 Мэв составляет ~ 0,5 барна и имеет фактически порог, равный 1,4 МэВ (см. рис. 5.2.1). Доля нейтронов в спектре деления (см. рис. 5.2.4), энергия которых превышает 1,4 Мэв, составляет не более 60 %. Максимально возможное сечение взаимодействия нейтронов с ядрами в области энергий 2 ÷ 6 Мэв не превышает геометрического сечения ядра σ_Σ = π R ² = π(1,4·10^-13 238 ^1/3)² ≈ 2,4 барн. Таким образом

.

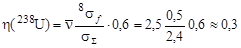(5.3.22)

Полное число нейтронов на один захваченный составит η = η(²³⁵U) + η(²³⁸U) = 0,3 +0,3 =0,6 < 1.

Отметим в заключение возможность самоподдерживаемой цепной реакции деления ядер ²³⁵U, возбуждаемой быстрыми нейтронами. Если в формулу (5.3.21) подставить величины для нейтронов с энергией ~ 2 МэВ: = 2,65; σ _а = 2,1 барн для ядер ²³⁵U; σ _а ≈ 0,1 барн для ядер ²³⁸U; ⁵σ _f = 2 барн для ядер ²³⁵U; то получим, что при ⁸ n /⁵ n < 30 (соответствует обогащению по ²³⁵U до 3 % и более) полное число вторичных нейтронов на один захваченный первичный превысит единицу даже без учета деления ядер ²³⁸U.

[1] Изомерами называются метастабильные ядра, имеющие период полураспада, отличный от периода полураспада ядра в основном состоянии.

[2] Плазмой называют газ, в котором 5 ÷ 10 % атомов или молекул находятся в ионизованном состоянии. С ростом температуры до ~ 10⁷ К газ становится полностью ионизованным и состоит из ядер и электронов.

Дата добавления: 2014-01-04