Теория подобия. 1. Подобны те явления, которые имеют одинаковую природу

1. Подобны те явления, которые имеют одинаковую природу.

2. Подобные явления описываются одинаковыми дифференциальными уравнениями и граничными условиями.

Для того, чтобы перенести данные, полученные на модели на реальный объект, необходимо, чтобы и объект и модель описывались абсолютно одинаковыми уравнениями. То есть уравнения должны быть инвариантными при подобных преобразованиях.

Критерий тепловых подобий Пекле:

(1.40)

где – определяющий размер (например, диаметр трубы).

У подобных явлений критерии равны:

или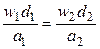

Все критерии безразмерны и имеют физический смысл. Критерий Пекле – отношение поля скоростей к полю температур.

Другие критерии получают из уравнения движения Навье – Стокса и граничных условий.

Критерий Рейнольдса – это отношение сил инерции к силам вязкости.

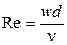. (1.41)

Значение критерия Рейносльдса определяет режим течения жидкости по трубам.

Если: <2300 – режим течения жидкости ламинарный;

2300<<10000 – переходный режим;

> 10000 – турбулентный режим.

Из критерия Пекле исключают скорость и получают критерий Прандтля

. (1.42)

Критерий Фрудта – отношение сил инерции к силам тяжести. 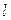– определяющий геометрический размер.

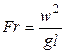. (1.43)

Из критерия Фрудта исключают скорость 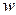и получают критерий Галилея

. (1.44)

Критерий Грасгофа

, (1.45)

где 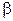– коэффициент объемного расширения.

Критерий конденсации (Кутателадзе)

, (1.46)

где – разность между температурой конденсации пара и температурой стенки со стороны конденсирующегося пара.

Все рассмотренные выше критерии называются определяющими.

Определяемый критерий должен содержать 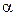– это критерий Нуссельта:

, (1.47)

где 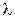– коэффициент теплопроводности пленки жидкости около стенки;

– определяющий геометрический размер.

Коэффициенты теплоотдачи рассчитываются из уравнения (1.47):

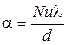. (1.47)

Уравнение для расчета критерия Нуссельта представляет собой зависимость между определяющими критериями. Для различных случаев теплоотдачи: при вынужденном течении жидкости, при конденсации пара, кипении, конвекции и т.д. уравнение для расчета критерия Нуссельта имеет различный вид и в него входят различные определяющие критерии.

Теплоотдача при вынужденном движении жидкости

Если жидкость течет по трубопроводу под действием различных внешних сил (например, создаваемых насосом), то движение – вынужденное. Для вынужденного движения справедлива теория пограничного слоя.

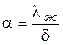
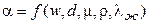
Вид зависимости 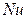от различен для каждого из трех режимов течения (рисунок 1.17).

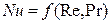. (1.48)

Для турбулентного режима течения (Re>10000):

. (1.49)

Для переходного режима течения (2300≤Re≤10000):

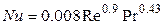. (1.50)

Для ламинарного режима течения (Re<2300):

. (1.51)

Рисунок 1.17 – Вид зависимости критерия Нуссельта от значения критерия Рейнольдса.

Дата добавления: 2014-01-04