Осаждение (отстаивание). Скорость осаждения

Осаждение применяется для грубого разделения суспензий под действием сил тяжести. Этот процесс проводится в аппаратах, называемых отстойниками. Для расчета отстойников необходимо рассчитать скорость осаждения, т.е. скорость движения твердых частиц в жидкости.

Для вывода формул расчета скорости осаждения рассмотрим движение твердой частицы шарообразной формы в неподвижной жидкости под действием сил тяжести. Если частица осаждается под действием сил тяжести, то скорость ее движения в жидкости сначала возрастает из-за ускорения свободного падения. Одновременно с увеличением скорости частицы будет расти сопротивление среды ее движению, поэтому ускорение частицы будет уменьшаться и через некоторое время станет равным нулю. При этом наступает равновесие действующих на частицу сил, и она будет двигаться равномерно с постоянной скоростью, которая и является скоростью осаждения.

Рассмотрим силы, действующие на осаждающуюся частицу в жидкости (рисунок 4.3).

По второму закону Ньютона

. (4.3)

Рисунок 4.3 – Силы, действующие на частицу при ее движении в вязкой среде:

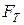– сила тяжести;

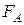– сила Архимеда (подъемная);

– сила сопротивления среды;

Мы рассматриваем мелкие частицы. Они очень быстро начинают двигаться равномерно с постоянной скоростью. Поэтому можно принять, что , т.е. разгона частиц почти нет или им пренебрегают ()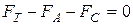

. (4.4)

, (4.5)

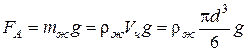, (4.6)

где – диаметр частицы; индекс «» – частица, «» – жидкость.

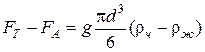. (4.7)

, (4.8)

где (дзета) – коэффициент сопротивления;

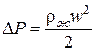
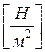
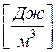– динамический напор или кинетическая энергия

омывания единицы объема;

– проекция частицы на плоскость, перпендикулярную направлению ее

движения. Т.к. частица – шар, то – площадь ее поперечного сечения.

Определение скорости осаждения. Подставим выражения (4.7) и (4.8) в (4.4)

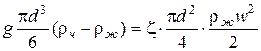. (4.9)

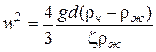, отсюда (4.10)

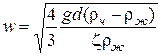. (4.11)

Для того, чтобы рассчитать по формуле (4.11) скорость осаждения необходимо знать величину . Коэффициент сопротивления зависит от режима обтекания частицы жидкостью. В логарифмических координатах зависимость 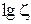от 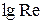имеет вид, представленный на рисунке 4.4. Расчет скорости по уравнению (4.11) проводят только методом последовательного приближения в следующем порядке:

1. задаются режимом осаждения;

2. подставляют в формулу (4.10) соответствующее режиму выражение вместо ;

3. из полученного уравнения рассчитывают скорость осаждения;

4. по скорости определяют значение критерия Рейнольдса и режим осаждения;

5. если режим получился другой, то заново пересчитывают скорость.

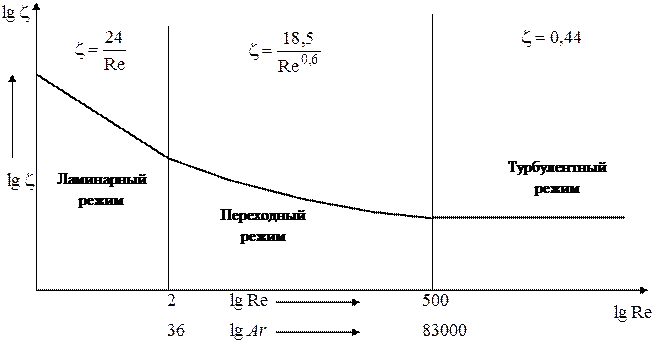
Рисунок 4.4 – Вид зависимости коэффициента сопротивления от критерия Рейнольдса для различных режимов осаждения частицы (в логарифмических координатах).

Рассмотренный выше метод расчета скорости осаждения не очень удобен и длителен. Поэтому для удобства использования в расчетной практике Лященко предложил другой метод. По этому методу скорость выражается из критерия Рейнольдса, возводится в квадрат и подставляется в уравнении (4.10) ().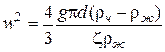

, (4.12)

,

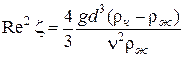, (4.13)

Примем за критерий Архимеда выражение

, (4.14)

Физический смысл критерия Архимеда заключается в том, что он учитывает соотношение сил тяжести, вязкости и силы Архимеда.

Получим критериальное уравнение для расчета скорости осаждения:

(4.15)

Порядок расчета скорости осаждения по методу Лященко.

1. Рассчитываем значение критерия Архимеда по выражению (4.14).

2. По 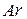определяем режим осаждения и выбираем формулу для расчета коэффициента сопротивления . Это возможно, так как согласно критериальному уравнению (4.15) между 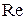и 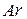есть однозначное соответствие. Но критерий Архимеда, в отличие от 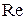, не зависит от скорости осаждения, а определяется только геометрическими размерами частицы и свойствами материала частицы жидкой среды.

Ламинарный режим движения

При ламинарном движении, наблюдающемся при небольших скоростях и малых размерах тел или при высокой вязкости среды, тело окружено пограничным слоем жидкости и плавно обтекается потоком (рисунок 4.5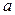). Потеря энергии в таких условиях связана в основном лишь с преодолением сопротивления трения. Критерий Рейнольдса .

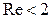Рисунок 4.5 – Движение частицы в жидкой среде при различных режимах: ламинарном (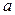), переходном (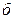) и турбулентном ().

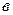Для ламинарного режима осаждения , подставим в выражение (4.15)

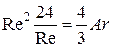; ; при .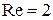

Таким образом, если 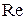< 2, то 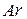< 36 - ламинарный режим осаждения (обтекания частицы).

Переходный режим движения

С увеличением скорости движения тела все большую роль начинают играть силы инерции. Под действием этих сил пограничный слой отрывается от поверхности тела, что приводит к понижению давления за движущимся телом в непосредственной близости от него и к образованию беспорядочных местных завихрений в данном пространстве (рисунок 4.5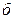). При этом разность давлений жидкости на переднюю (лобовую) поверхность тела, встречающую обтекающий поток, и на его заднюю (кормовую) поверхность все больше превышает разность давлений, возникающую при ламинарном обтекании тела.

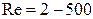
Для переходного режима осаждения 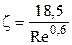, подставим в выражение (4.15)

; при .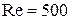

Т.о., если 2<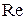< 500, то 36<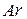< 83000 – переходный режим.

Турбулентный режим движения

При 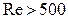роль лобового сопротивления становится преобладающей, а сопротивлением трения можно пренебречь. За частицей возникает вихревая дорожка (турбулизация), рисунок 4.5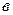. Наступает автомодельный режим. Коэффициент сопротивления .

При турбулентном режиме осаждения

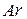> 83000 и 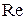> 500.

3. Подставим в формулу (4.15) () соответствующее режиму выражение для и рассчитаем значение .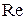

4. Рассчитаем скорость осаждения по выражению .

Рассчитанная скорость – скорость осаждения одиночной частицы шарообразной формы. В реальных условиях частицы имеют сложную форму (отличную от шарообразной) и осаждение – коллективный процесс, т.е. стесненное осаждение. В результате этого реальная скорость осаждения частиц отличается от расчетной. Поэтому для определения реальной скорости необходимо к расчетному ее значению ввести поправки:

, (4.16)

где 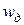– действительная скорость осаждения;

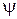– коэффициент формы. Как правило, 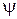<1. Для частиц круглой формы 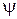=1;

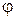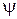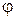– коэффициент стесненности осаждения. Зависит от концентрации частиц в растворе. и определяются по справочнику.

Дата добавления: 2014-01-04