Режимы фильтрования

На практике встречаются три основных режима процесса фильтрования.

1. При постоянной движущей силе (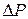=const).

2. При постоянной скорости фильтрования (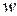=const).

3. При переменных 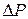и .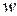

Режим № 1 осуществляется в вакуум-фильтрах, а также при создании избыточного давления над суспензией с помощью сжатого воздуха. Режим № 2 можно получить с помощью поршневого насоса. Если для подачи суспензии используется центробежный насос, то реализуется режим № 3. Однако, если при этом на линии подачи суспензии установить регулируемый вентиль, которым поддерживать постоянную 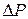, то можно обеспечить режим №1.

Режим фильтрования при 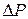=const

Запишем основное дифференциальное уравнение фильтрования (4.37) в виде:

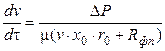, (4.38)

где 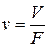– удельный объем фильтрата (количество фильтрата, образовавшееся с 1 м² площади фильтровальной перегородки).

Выразим сопротивление фильтровальной перегородки через равное ему сопротивление слоя осадка:

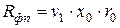, (4.39)

где – константа, которая показывает удельный объем фильтрата, необходимый для образования осадка, сопротивление которого равно сопротивлению фильтровальной перегородки. Получим зависимость:

. (4.40)

Запишем выражение (4.40) в виде:

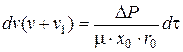. (4.41)

Проинтегрируем (4.41) в пределах от = 0 до и от = 0 до 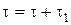. – это время, необходимое для получения объема фильтрата , в результате чего образуется осадок, сопротивление которого равно сопротивлению фильтровальной перегородки.

,

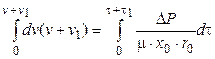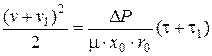, (4.42)

.

Обозначим за константу фильтрования выражение

. (4.43)

Запишем выражение (4.42) с учетом (4.43):

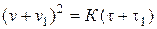. (4.44)

Выражения (4.42) и (4.43) являются уравнением фильтрования в интегральной форме при 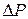=const. Проанализируем этот режим фильтрования (рисунок 4.12).

С течением времени скорость фильтрования 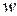уменьшается по нелинейному закону (т.к. сопротивление осадка увеличивается), а удельный объем фильтрата и высота слоя осадка 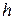увеличиваются по нелинейному закону.

Выражение (4.44) используется для расчета фильтров. Если дано время фильтрования и объем фильтрата, то может быть рассчитана площадь поверхности фильтрования. В случае расчета фильтрпресса, например, может быть определено время заполнения межрамного пространства осадком, если задана поверхность фильтрования.

Рисунок 4.12 – Зависимость параметров процесса фильтрования от времени в режиме с постоянной движущей силой 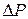(разностью давлений).

Величины , 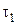в уравнении фильтрования (4.44) называются константами фильтрования, их значения определяются по экспериментальным данным следующим образом.

Продифференцируем уравнение (4.44) и получим

,

. (4.45)

Заменим производную отношением конечных разностей:

,

где 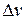– изменение удельного объема фильтрата за интервал времени .

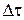В координатах 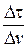–уравнение (4.45) имеет вид прямой линии. Проводят эксперимент по фильтрованию, определяя 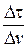при различных значениях , наносят на график экспериментальные точки (рисунок 4.13).

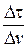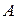Через точки проводят прямую до пересечения с осью . Проанализируем уравнение (4.45). Если =0, то , т.е. равен длине отрезка (– число), отсекаемого прямой на оси :

. (4.46)

При 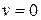получим:

,

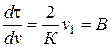где – отрезок, отсекаемый прямой на оси ординат. Отсюда

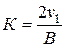. (4.47)

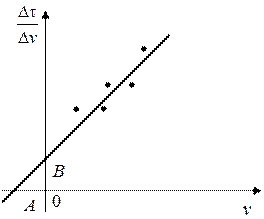Рисунок 4.13 – График зависимости 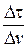от (к определению констант фильтрования графоаналитическим способом).

При имеем 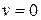. Из уравнения (4.44) следует, что

. (4.48)

Таким образом, по выражению (4.46) находится значение константы , затем по (4.47) определяется константа фильтрования и после этого по (4.48) определяется константа .

Режим фильтрования при 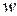=const

Для фильтрования при постоянной скорости производную 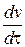можно заменить отношением удельного объема фильтрата ко времени фильтрования.

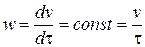. (4.49)

Тогда основное дифференциальное уравнение фильтрования (4.37) можно записать в виде

,

, (4.50)

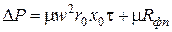. (4.51)

В уравнении (4.51) все величины постоянны, кроме 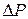и . Значит, при постоянной скорости фильтрования (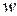=const) 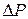будет меняться в зависимости от времени фильтрования по линейному закону: (рисунок 4.14).

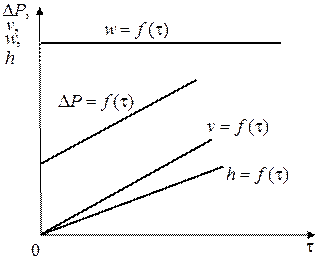Рисунок 4.14 – Зависимость параметров процесса фильтрования от времени в режиме с постоянной скоростью фильтрования.

Дата добавления: 2014-01-04