Неидеальные растворы и азеотропные смеси

Реальные смеси не подчиняются закону Рауля. А газовая фаза не подчиняется уравнению Менделеева – Клапейрона (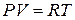). В идеальном газе мольная доля равна объемной, так как мольный объем одинаков для всех компонентов (1 моль газа – 22,4 л).

Равновесие в некоторых неидеальных смесях может быть описано уравнением:

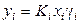. (5.15)

Коэффициент активности 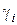зависит от энергии взаимодействия между молекулами и их размера, т.е. от их объема и поверхности. 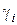может быть больше или меньше 1 (для идеальных смесей 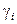=1). Это называют отрицательным или положительным отклонением от закона Рауля.

Однако, неидеальность большинства реальных систем настолько велика, что равновесие в них не может быть описано уравнением (5.15) и другими аналитическими уравнениями. Для таких смесей равновесные данные приводятся в справочниках в виде таблиц зависимости равновесных составов паров и жидкости.

Отклонения от идеальности бывают настолько большими, что получаются азеотропные и расслаивающиеся смеси.

Азеотропная – такая смесь, у которой при некотором составе жидкости равновесный пар имеет такой же состав, то есть в точке азеотропа 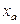= 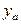(рисунок 5.5).

До точки азеотропа низкокипящий компонент является ЛЛК, при этом >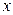. После точки азеотропа низкокипящий компонент – ТЛК, <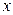. В точке азеотропа = 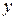и разделение смеси невозможно ни перегонкой, ни ректификацией.

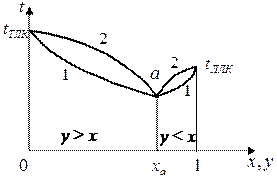Рисунок 5.5 – Диаграмма 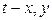для азеотропной смеси:

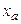– состав смеси, соответствующий точке азеотропа 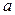, в которой = .

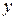Диаграмма

Задаваясь различными температурами из диаграммы 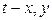определяют множество значений соответствующих и 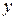. Наносят точки с координатами (;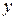) на диаграмму и соединяем их плавной кривой. Полученная кривая 1 – равновесная кривая системы «пар–жидкость» .

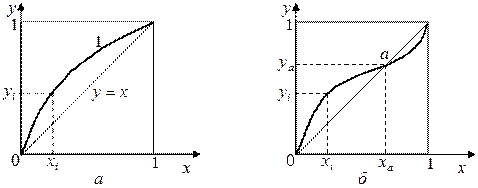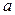Рисунок 5.6 – Диаграмма для идеальной смеси () и азеотропной смеси ().

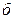Дата добавления: 2014-01-04