
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Расчет простой перегонки
|
|
|
|
Сложность расчета процесса периодической перегонки заключается в постоянно изменяющихся составах кубовой жидкости и дистиллята.
Если в кубе в данный момент времени  кмоль жидкости концентрацией по ЛЛК
кмоль жидкости концентрацией по ЛЛК 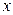 кмоль/кмоль, то через время
кмоль/кмоль, то через время  смеси останется
смеси останется 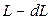 , а ее концентрация станет равной
, а ее концентрация станет равной 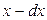 (так как
(так как  =
=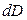 , то
, то  =
= ).
).
В исходной смеси было 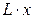 ЛЛК, стало
ЛЛК, стало 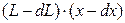 . Из уравнения материального баланса по ЛЛК имеем:
. Из уравнения материального баланса по ЛЛК имеем:
 . (5.21)
. (5.21)
Раскроем скобки и учтем, что состав дистиллята  и состав паров, равновесных с жидкостью
и состав паров, равновесных с жидкостью  одинаковы, следовательно
одинаковы, следовательно 
 .
.
Произведением  пренебрегаем как бесконечно малой величиной второго порядка, получим
пренебрегаем как бесконечно малой величиной второго порядка, получим
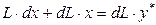 ,
,
 ,
,
 . (5.22)
. (5.22)
Дифференциальное уравнение (5.22) проинтегрируем в пределах изменения количества жидкости в кубе  от начального
от начального  до конечного
до конечного  и соответствующего изменения в ней содержания целевого компонента
и соответствующего изменения в ней содержания целевого компонента 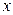 от
от  до
до  .
.
 ,
,
 . (5.23)
. (5.23)
Из уравнения (5.23) находят количество кубового остатка  , если задана его концентрация
, если задана его концентрация  .
.
Вид функции  определяется формой равновесной кривой и обычно не может быть установлен аналитически для каждого конкретного случая перегонки. Поэтому интегрирование правой части уравнения (5.23) проводят графически – построением зависимости
определяется формой равновесной кривой и обычно не может быть установлен аналитически для каждого конкретного случая перегонки. Поэтому интегрирование правой части уравнения (5.23) проводят графически – построением зависимости 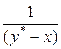 от
от 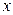 (рисунок 5.11). По площади под кривой, ограниченной ординатами
(рисунок 5.11). По площади под кривой, ограниченной ординатами  и
и  определяют (зная масштаб диаграммы) величину искомого интеграла.
определяют (зная масштаб диаграммы) величину искомого интеграла.
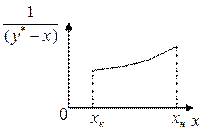 |
Рисунок 5.11 – Зависимость 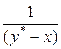 от
от 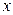 .
.
Перегонка с водяным паром (инертным газом)
Этот вид перегонки применяют для разделения смесей веществ, не растворимых в воде, кипящих при высоких температурах и не обладающих при температурах кипения достаточной термической стойкостью. Перегонка с водяным паром позволяет заметно снизить температуру кипения смеси и избежать разложения и осмоления компонентов. При перегонке с водяным паром высококипящих веществ, не растворимых в воде, температура кипения смеси ниже температуры кипения воды при данном давлении. Таким образом, при атмосферном давлении температура перегонки будет ниже 100 0С.
Перегонка с водяным паром применяется при переработке жирных кислот, эфирных масел, смол, для дезодорации – удаления веществ, обуславливающих неприятный запах масел, жиров и других продуктов.
 Рассмотрим технологическую схему процесса перегонки с водяным паром (рисунок 5.12).
Рассмотрим технологическую схему процесса перегонки с водяным паром (рисунок 5.12).

Рисунок 5.12 – Технологическая схема процесса перегонки с водяным паром:
1 – перегоны куб; 2 – барботер; 3 – конденсатор; 4 – сепаратор.
Исходная смесь загружается в куб 1, обогреваемый глухим паром через рубашку. Внутрь куба через барботер 2 подается острый пар. Пары, образующиеся при испарении смеси, направляются в конденсатор-холодильник 3. Образовавшийся конденсат поступает в сепаратор 4, где нерастворимые друг в друге жидкости расслаиваются. Снизу сепаратора через гидравлический затвор удаляется вода, а сверху – отогнанный целевой компонент (ЛЛК), не растворимый в воде.
Система, состоящая из двух взаимно нерастворимых компонентов и трех фаз (двух жидких и одной паровой), согласно правилу фаз Гиббса, обладает одной степенью свободы ( ). Отсюда следует, что каждой температуре смеси отвечает строго определенное давление, и каждый компонент смеси ведет себя независимо от другого. Соответственно парциальное давление каждого компонента не зависит от его содержания в смеси и равно давлению насыщенных паров чистого компонента при этой же температуре:
). Отсюда следует, что каждой температуре смеси отвечает строго определенное давление, и каждый компонент смеси ведет себя независимо от другого. Соответственно парциальное давление каждого компонента не зависит от его содержания в смеси и равно давлению насыщенных паров чистого компонента при этой же температуре: 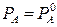 ;
; 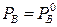 (рисунок 5.13).
(рисунок 5.13).
 | |||
 | |||
Рисунок 5.13 – Диаграммы зависимости  от
от 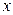 (
(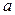 ),
),  от
от 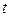 (
(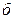 ) и
) и  для систем, состоящих из двух взаимно нерастворимых компонентов и трех фаз:
для систем, состоящих из двух взаимно нерастворимых компонентов и трех фаз:
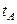 ,
,  =100 0С и
=100 0С и  – температуры кипения при атмосферном давлении нерастворимого в воде компонента, воды и их смеси.
– температуры кипения при атмосферном давлении нерастворимого в воде компонента, воды и их смеси.
Вывод, у смесей с нерастворимыми компонентами:
- парциальное давление паров и их состав не зависят от состава жидкости.
- температура кипения смеси не зависит от концентрации в ней компонентов;
- температура кипения смеси ниже, чем температура кипения чистых веществ;
Это свойство используется в производстве для снижения температуры кипения термолабильных смесей при перегонке с водяным паром или инертным носителем (газом), т.е. компонентом, нерастворимым в исходной смеси. Для понижения температуры кипения смесей также применяют вакуум.
Теоретический расход водяного пара на процесс может быть найден из следующих соотношений. По закону Дальтона
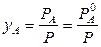 ;
; 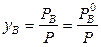 и
и  .
.
При постоянной температуре давления насыщенных паров чистых компонентов  и
и  постоянны и, следовательно, постоянно отношение
постоянны и, следовательно, постоянно отношение  . Соотношение между количествами
. Соотношение между количествами  и
и  компонентов в парах определяется следующим образом:
компонентов в парах определяется следующим образом:
 ,
,
где  и
и  – массовые расходы отгоняемого компонента и водяного пара;
– массовые расходы отгоняемого компонента и водяного пара;
 и
и  – молекулярные массы отгоняемого компонента и водяного пара;
– молекулярные массы отгоняемого компонента и водяного пара;
Безразмерный комплекс  называется критерием состава и входит в критериальные уравнения, описывающие массообмен при перегонке в токе с водяным паром. Расход водяного пара
называется критерием состава и входит в критериальные уравнения, описывающие массообмен при перегонке в токе с водяным паром. Расход водяного пара 
 . (5.24)
. (5.24)
Как правило, пар извлекаемым компонентом не насыщается и в приведенное уравнение вводят коэффициент насыщения 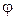 = 0,5 – 0,9.
= 0,5 – 0,9.
 . (5.25)
. (5.25)
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1000; Нарушение авторских прав?; Мы поможем в написании вашей работы!