Властивість згортки

Якщо оригінали і , то

Таблиця зображень і оригіналів

Використовуючи перетворення Лапласа, а також властивості зображень, складаємо таблицю (7.1)

Таблиця 7.1 – оригінали і відповідні їм зображення

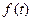
№	Оригінал	Зображення

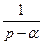
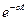
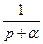
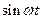
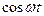
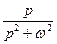
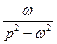
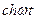
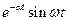
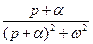
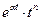
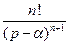
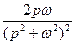
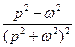
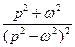
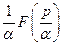
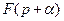
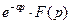
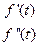
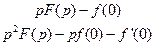
7.3 Схема побудови розв’язку диференційного рівняння з частинними похідними

Наведемо схему побудови розв’язку диференційного рівняння з частинними похідними, де шукана функція 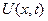залежить лише від двох змінних і 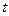. Нехай вона задовольняє рівняння:

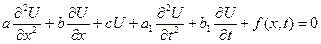, (7.2)

де 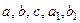– неперервні функції від , задані на проміжку . Нехай треба знайти розв’язок рівняння (7.2) для напівнескінченної смуги: , , 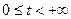що задовольняє задані додаткові умови

П.У.

К.У. (7.3)

де – сталі.

Задача (7.2) – (7.3) нестаціонарна, оскільки шуканий розв’язок істотно залежить від початкових умов і описує так званий неусталений перехідний режим фізичного процесу.

Застосуємо перетворення Лапласа до функції 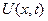за змінною 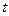. Вважаємо, що функці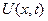ї , і 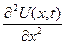є оригіналами.

Позначивши зображення шуканої функції через , запишемо наступні співвідношення:

, , .

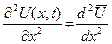Тут розглядається як параметр.

Для знаходження зображень частинних похідних по 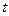застосуємо теорему про диференціювання оригіналу. Одержимо

,

.

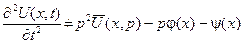Вважатимемо, що – оригінал, тоді крайові умови у просторі зображень матимуть вигляд

(7.4) (3)

де .

Таким чином, вважаючи, що 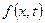є оригіналом, операційний метод приводить розв’язання поставленої нестаціонарної задачі (7.2)–(7.3) до розв’язання звичайного диференціального рівняння другого порядку

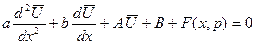(7.5)

з крайовими умовами (7.4), де , , 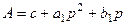, 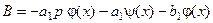– комплексний параметр.

Приклад 7.1 Кінці струни і закріплені жорстко. Початкове відхилення задано рівністю 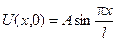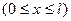, початкова швидкість рівна нулю. Знайти відхилення 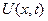при .

Задача зводиться до розв’язання диференційного рівняння

,

яке задовольняє задані додаткові умови

П.У. К.У.

Застосуємо перетворення Лапласа до функції 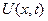за змінною 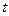. Позначивши зображення шуканої функції через , запишемо наступні співвідношення:

, , ,

,

.

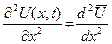Тоді на основі цих співвідношень та сформульованої задачі з додатковими умовами, одержимо у просторі зображень наступну задачу

, (7.6)

К.У.

Розв’язок лінійного неоднорідного диференціального рівняння другого порядку шукаємо у вигляді:

,

де – загальний розв’язок відповідного однорідного рівняння .

Характеристичне рівняння 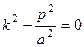. Звідси

.

Тоді загальний розв’язок однорідного рівняння буде

.

Частинний розв’язок неоднорідного рівняння знайдемо у вигляді .

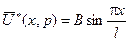Для знаходження невідомої сталої підставимо частинний розв’язок у (7.6) та отримаємо рівняння

.

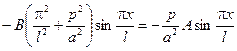Звідси

.

Тоді

Загальний розв’язок рівняння буде мати вигляд:

.

Підставляючи розв’язок у крайові умови, знайдемо невідомі константи

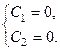
Отже, оригіналом для з врахуванням формули оберненого перетворення

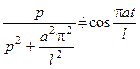
буде функція

,

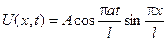яка є розв’язком поставленої задачі.

Приклад 7.2 Знайти розв’язок рівняння теплопровідності , який задовольняє початковим і граничним умовам (), .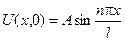

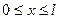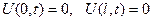Задача зводиться до розв’язання диференційного рівняння

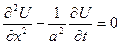, яке задовольняє задані додаткові умови

П.У. , К.У.

Застосуємо перетворення Лапласа до функції 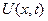за змінною 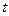. Позначивши зображення шуканої функції через , запишемо наступні співвідношення:

, , ,

.

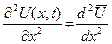Вихідне рівняння після підстановки отриманих формул та крайові умови у просторі зображень набудуть вигляду

,

К.У.

Розв’язок отриманого лінійного неоднорідного диференціального рівняння другого порядку шукатимемо у вигляді:

,

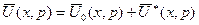де – загальний розв’язок відповідного однорідного рівняння:

,

характеристичне рівняння:

.

Звідси

.

Тоді загальний розв’язок однорідного рівняння буде

.

Частинний розв’язок неоднорідного рівняння знайдемо у вигляді

.

Для знаходження невідомої сталої підставимо частинний розв’язок у (7.6) та отримаємо рівняння

.

Звідси .

Тоді, .

Загальний розв’язок рівняння буде мати вигляд:

.

Підставляючи розв’язок у крайові умови, знайдемо невідомі константи

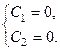
Отже, оригіналом для з врахуванням формули оберненого перетворення

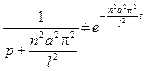
буде функція

,

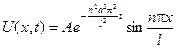яка і буде розв’язком поставленої задачі.

Дата добавления: 2014-01-04