
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Визначення потрібної надлишковості. Визначення шляхів її зменшення
|
|
|
|
Із викладеного вище витікає, що надлишковість коду визначається кількістю символів контрольної ознаки (k) та їх розрядністю (b). Прагнучи зменшувати надлишковість, потрібно зменшувати і їх значення.
Виходячи із того, що кількість спотворень в інформаційному об’єкті із n символів може бути в межах від tсп = 0 до tсп = n, визначимо кількість перевірочних символів, необхідну для виявлення tс спотворень. Для цього необхідно, щоб за допомогою k перевірочних символів можна було описати наступні ситуації:
спотворення відсутні −  − 1 випадок,
одиночне спотворення − − 1 випадок,
одиночне спотворення −  випадків,
двократне спотворення − випадків,
двократне спотворення −  випадків,
………………………………………..
спотворення кратності tсп - випадків,
………………………………………..
спотворення кратності tсп - 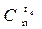 випадків. випадків.
|
Таким чином, загальна кількість спотворень кратності tс і менше дорівнює  звідки мінімальне необхідне число перевірочних символів для виправлення спотворень кратності tсп і менше визначається з наступної нерівності:
звідки мінімальне необхідне число перевірочних символів для виправлення спотворень кратності tсп і менше визначається з наступної нерівності:
2 k ≥  звідкіля k ≥ log2
звідкіля k ≥ log2  . (10)
. (10)
Нашим звичайним бажанням є − мати такий код, який дозволяє виправити усі можливі спотворення, тобто tсп = n. Тоді, використовуючи властивості суми коефіцієнтів бінома Ньютона, одержимо:
k ≥ log2 = log2 2 n = n,
= log2 2 n = n,
k ≥ m + k,
що є неможливим.
Виходом з цієї ситуації є постановка задачі виявлення або виявлення і виправлення не будь-яких спотворень в початковому коді, а тільки всіх можливих в заданих умовах. Іншими словами відповідний завадостійкий код слід орієнтувати на реальну статистику спотворень в каналі передачі (у ЗП даного типа), коли число спотворених символів tс = n · Рсп, де Рсп − ймовірність спотворення символу в каналі передачі (ЗП).
Додатковим обмеженням, яке сприяє зменшенню необхідної надлишковості коду можуть бути обмеження числа спотворень одним символом (бітом) в двійкових кодах або одним символом в групових (узагальнених) кодах. У ситуаціях, коли виправлення спотворення в одному символі є недостатнім (число спотворень в БКС більше за одне), використовують інші коди чи різні прийоми декореляції спотворень (див. нижче).
Приклад. Кодова комбінація містить m = 10 інформаційних бінарних елементів. Визначити необхідне число перевірочних одиничних елементів для виправлення будь-якого двократного спотворення.
Рішення. Вираз (9) для заданих умов матиме вигляд
k ≥ log2 ( ) або 2 k ≥ 1 + n + [ n (n − 1)]/4. (11)
) або 2 k ≥ 1 + n + [ n (n − 1)]/4. (11)
Примітка. З формул (10) і (11) можна визначити нижню теоретичну межу числа надлишкових символів. Практично ж кількість надлишкових символів перевищує вказане число.
Першим шляхом зменшення надлишковості, який є найбільш зрозумілим, є застосування вагових коефіцієнтів, які задовольняють умові (9) 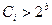 та, одночасно, є найменшими. Цій умові задовольняють вагові коефіцієнти, які вибирають із умови:
та, одночасно, є найменшими. Цій умові задовольняють вагові коефіцієнти, які вибирають із умови:
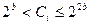 ,
,
тобто такі, що потребують для свого відображення не більше двох узагальнених символів.
Оскільки вагові коефіцієнти є такими, що потребують для свого представлення як мінімум двох символів, при розрахунку контрольної ознаки кожен із доданків у виразі (2) потребує для свого представлення трьох символів, а сама контрольна ознака – чотирьох, що, у свою чергу, знов може бути обмеженням для застосування такого коду.
Аналіз особливостей побудови деяких із відомих завадостійких кодів підказує наявність другого шляху зменшення потрібної надлишковості, який застосовано при побудові цих кодів. Таким шляхом є застосування при обчисленні контрольної ознаки додавання за певним модулем. При цьому вираз (2) для розрахунку контрольної ознаки набуває вигляду:
 (mod Р), (12)
(mod Р), (12)
де Р – значення обраного модуля.
Примітка. Звернемо увагу на те, що вираз (12) є генератором принаймні декількох кодів. Це досягається різними варіаціями із зміною розрядності груп (b), способу додавання, величин вагових коефіцієнтів  , та модуля Р. Наприклад, при
, та модуля Р. Наприклад, при  , b = 1 та Р = 2 маємо код із контролем на парність; при
, b = 1 та Р = 2 маємо код із контролем на парність; при  , b > 1 та Р =
, b > 1 та Р =  маємо код із контрольним додаванням; при
маємо код із контрольним додаванням; при 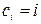 ,
,
b = 1, використанні порозрядного додавання по модулю Р = 2 маємо варіант коду Хеммінга та т. інш.
Аналіз виразу (12) показує, що зміною розрядності груп (b), способу додавання, величин вагових коефіцієнтів  , та модуля Р також можна зробити величину потрібну надлишковість досить малою. Обмеженням при цьому є таке значення модуля, яке дозволяє забезпечити безпомилкове визначення як місця, так і величини можливого спотворення в інформаційному об’єкті. Для визначення цих обмежень знову, виходячи із виразу (12), розглянемо процедуру декодування за умовою забезпечення можливостей із виявлення факту наявності, місця та величини можливих спотворень.
, та модуля Р також можна зробити величину потрібну надлишковість досить малою. Обмеженням при цьому є таке значення модуля, яке дозволяє забезпечити безпомилкове визначення як місця, так і величини можливого спотворення в інформаційному об’єкті. Для визначення цих обмежень знову, виходячи із виразу (12), розглянемо процедуру декодування за умовою забезпечення можливостей із виявлення факту наявності, місця та величини можливих спотворень.
Як і раніше, при декодуванні слід здійснити розрахунок контрольної ознаки ( (mod Р)), де
(mod Р)), де  – значення одержаних символів цієї інформаційної послідовності. Цю величину
– значення одержаних символів цієї інформаційної послідовності. Цю величину  слід порівняти із контрольною ознакою, яка була сформована попередньо (
слід порівняти із контрольною ознакою, яка була сформована попередньо ( (mod Р)). Для порівняння достатньо обрахувати різницю цих контрольних ознак:
(mod Р)). Для порівняння достатньо обрахувати різницю цих контрольних ознак:
 (mod Р). (13)
(mod Р). (13)
Зрозуміло, що при відсутності спотворень в одержаній інформаційній послідовності відповідні значення символів  та
та 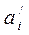 у виразі (13) є однаковими, в наслідок чого різниця цих контрольних ознак дорівнює нулю. При наявності спотворень в одному із символів (нехай це буде
у виразі (13) є однаковими, в наслідок чого різниця цих контрольних ознак дорівнює нулю. При наявності спотворень в одному із символів (нехай це буде  ) ця різниця є відмінною від нуля. Дійсно, у цьому випадку перший доданок у виразі (13) набуде вигляду
) ця різниця є відмінною від нуля. Дійсно, у цьому випадку перший доданок у виразі (13) набуде вигляду

а отже вираз (13) набуде значення:
 (mod Р) =
(mod Р) =  (mod Р) ≠ 0, (13)
(mod Р) ≠ 0, (13)
Це і є синдромом спотворення. Звернемо увагу на те, що максимальне значення добутку  , як і доданків у виразі (1), потребує для свого представлення трьох символів. Це означає, що для забезпечення визначення правильного значення величини
, як і доданків у виразі (1), потребує для свого представлення трьох символів. Це означає, що для забезпечення визначення правильного значення величини  як мінімальне значення модуля Р можна використати величину Р = 23 b , і тоді
як мінімальне значення модуля Р можна використати величину Р = 23 b , і тоді
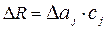 (mod Р) =
(mod Р) =  .
.
Для визначення місця і величини спотворення слід здійснити послідовне ділення синдрому спотворення  на кожен із вагових коефіцієнтів
на кожен із вагових коефіцієнтів  та визначити при цьому значення можливого спотворення
та визначити при цьому значення можливого спотворення  :
:
 . (5)
. (5)
Неважко зрозуміти, що правильне значення спотворення є цілою величиною, яка до того ж є меншою за максимальне значення групи 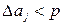 . Отже, за рахунок вибору вагових коефіцієнтів, бажано добитися таких результатів, коли при виконанні операції (5) в разі ділення не на
. Отже, за рахунок вибору вагових коефіцієнтів, бажано добитися таких результатів, коли при виконанні операції (5) в разі ділення не на 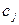 , а на будь який інший ваговий коефіцієнт
, а на будь який інший ваговий коефіцієнт  (і = 1, 2, …, m) результат розподілу є дробовим числом. В цьому разі вираз (5) набуде виду
(і = 1, 2, …, m) результат розподілу є дробовим числом. В цьому разі вираз (5) набуде виду
 .
.
Зрозуміло, що дробове значення результату розподілу визначається лише співвідношенням усіх можливих пар вагових коефіцієнтів і може бути гарантовано забезпеченим лише тоді, коли вагові коефіцієнти є взаємно простими числами.
Отже, наявність цілого значення результату ділення свідчить про виявлення місця спотворення і, із врахуванням виразу (2), його корекція, є примітивною операцією:
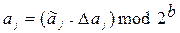 .
.
Наявність же дробового значення результату ділення свідчить про відсутність спотворення в даній групі і необхідності продовжити пошуки.
Зрозуміло, що використання як вагових коефіцієнтів лише простих чисел при їх заданій розрядності зменшує їх можливу кількість, але це зменшення при значних розрядностях груп не є суттєвим обмеженням. Наприклад, при використанні символів байтової довжини b = 8 (1 байт) кількість простих чисел, які можна використати як двобайтові вагові коефіцієнти (тоді  ), навіть у взятому із довідника [4] в суттєво обмеженому діапазоні (
), навіть у взятому із довідника [4] в суттєво обмеженому діапазоні ( ), налічує більше ніж 700. Тоді, наприклад, для протоколів ІР та ТСР, можна забезпечити передачу дейтаграм із максимальним розміром 65536 байтів із виявленням та виправленням спотворень при глибині перемежування менше ніж 93. Можна очікувати, що вибір простих чисел із ширшого діапазону (
), налічує більше ніж 700. Тоді, наприклад, для протоколів ІР та ТСР, можна забезпечити передачу дейтаграм із максимальним розміром 65536 байтів із виявленням та виправленням спотворень при глибині перемежування менше ніж 93. Можна очікувати, що вибір простих чисел із ширшого діапазону ( ) дозволить суттєво зменшити цю глибину перемежування (приблизно до 9 – 10).
) дозволить суттєво зменшити цю глибину перемежування (приблизно до 9 – 10).
|
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 450; Нарушение авторских прав?; Мы поможем в написании вашей работы!