
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Виробнича функція Коба-Дугласа
|
|
|
|
Виробничі функції, загальні положення
Виробнича функція Коба-Дугласа
Виробничі функції, загальні положення
- Еластичність заміни факторів
- Виробнича функція CES
- Моделювання за допомогою ВФ
Моделі, які ми розглядали дотепер були лінійні. Без сумніву, охопити лінійними моделями всю складність сучасних економічних процесів неможливо. Складність полягає ще і в тому, що для того, щоб побудувати, наприклад, модель Неймана, необхідно зібрати дуже багато статистичної інформації, яка враховує всю внутрішню структуру виробництва.
З другого боку, як правило, простіше отримати звітні дані про узагальнені економічні показники такі як вартість виробленого продукту, об’єм основних фондів, чисельність працівників і т.д. Виявляється, що оперуючи лише такими узагальненими даними і розглядаючи виробничий об’єкт як „чорний ящик”, тобто розглядаючи лише зв’язок між затраченими засобами і виробленим продуктом, теж можна отримати змістовний результат.
Ці міркування і є основою теорії виробничих функцій. Ця теорія бере свій початок від 1928 року коли була опублікована стаття американських вчених - математика Коба і економіста Дугласа «Теорія виробництва», яка і була початком для розвитку нелінійних моделей, зокрема нелінійних виробничих функцій. В цій статті було зроблено спробу емпіричним шляхом визначити вплив залежності величини витраченого капіталу і праці на об’єм виробленої продукції в обробній промисловості США. На основі інформації про капіталовкладення і ресурси робочої сили будується функція для визначення обсягу випуску продукції.
На основі зібраних емпіричних даних 1899-1922рр.було проведено відповідний аналіз і поставлено 3 наступні задачі:
1. Визначити параметричний клас функцій, які найточніше наближають кількісні співвідношення між трьома обраними характеристиками виробничої діяльності;
2. Знайти числові параметри для конкретної функції з заданого класу;
3. Перевірити адекватність моделі (чи наша побудована функція достатньо добре описує експериментальні дані).
Коб запропонував функцію виду
 - (1)
- (1)
де У - обсяг виробленої продукції;
 – капіталовкладення
– капіталовкладення
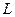 – трудові ресурси
– трудові ресурси
 ,
,  ,
, 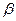 - числові параметри
- числові параметри
 ,
,  ,
, 
Було складено систему рівнянь
 ,
, 
де  фактичні значения відповідних величин в рік
фактичні значения відповідних величин в рік  . Методом найменших квадратів було знайдено значення параметрів
. Методом найменших квадратів було знайдено значення параметрів  ,
,  ,
, 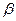 , які відповідно мінімізували вираз
, які відповідно мінімізували вираз
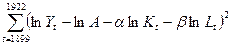
При цьому з’ясувалось, що 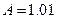 ,
, 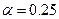 ,
, 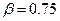 ;
;
Тобто було встановлено, що  .
.
Перевірка адекватності моделі 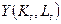 з фактичними даними засвідчила, що отримана залежність дає дуже хороше наближення, а найбільші відхилення величин
з фактичними даними засвідчила, що отримана залежність дає дуже хороше наближення, а найбільші відхилення величин  і
і 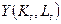 спостерігались тільки в періоди економічної депресії або надмірного оживлення ділової активності.
спостерігались тільки в періоди економічної депресії або надмірного оживлення ділової активності.
В науковому плані це був чудовий старт і зараз теорія виробничих функцій дуже широко застосовується для задач планування і прогнозування як в окремих галузях, так і на рівні всього народного господарства.
Для вивчення основних математичних характеристик виробничих функцій і їх економічної інтерпретації розглянемо двох факторну функцію
 (2)
(2)
де  - мають той самий смисл, що і в функції Коба-Дугласа (1). Функцію (1) ми будемо і надалі використовувати в якості практичної ілюстрації.
- мають той самий смисл, що і в функції Коба-Дугласа (1). Функцію (1) ми будемо і надалі використовувати в якості практичної ілюстрації.
На виробничу функцію (2) накладаються наступні умови:
1)  ; (3)
; (3)
2)  ,
,  ; (4)
; (4)
3) 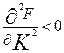 ,
,  ; (5)
; (5)
4)  ,
,  ,
, 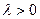 (6)
(6)
Коротко пояснимо накладені вимоги:
(3) – при відсутності одного з факторів виробництва, випуск продукції неможливий;
(4) – при збільшенні об’єму одного з факторів, якщо інший – незмінний, випуск продукції зростає;
(5) – якщо один з факторів зафіксувати, то збільшення приросту другого фактора призводить до зменшення термінів приросту випуску продукції;
(6) – умова однорідності степені  . Показник
. Показник  характеризує ефект від розширення масштабу виробництва. Якщо
характеризує ефект від розширення масштабу виробництва. Якщо  >1, то одночасне збільшення всіх факторів в
>1, то одночасне збільшення всіх факторів в  разів, призводить до зростання об’єму випуску більше ніж в
разів, призводить до зростання об’єму випуску більше ніж в  разів.
разів.
На практиці найчастіше  .
.
Розглянемо основні економіко-математичні характеристики виробничих функцій;:
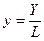 - середня (питома) продуктивність праці; (7)
- середня (питома) продуктивність праці; (7)
 - середня (питома) фондовіддача; (8)
- середня (питома) фондовіддача; (8)
 - гранична продуктивність праці; (9)
- гранична продуктивність праці; (9)
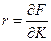 - гранична фондовіддача; (10)
- гранична фондовіддача; (10)
 - фондоозброєність (кількість капіталовкладень на одного працівника);
- фондоозброєність (кількість капіталовкладень на одного працівника);
Всі перераховані показники є розмірними величинами, зв’язаними з абсолютними приростами. Представляють інтерес величини, які характеризують процент приросту продукції при збільшенні затрат ресурсу на 1 %. Такі показники називаються коефіцієнтами еластичності.
Коефіцієнт еластичності по фондах:
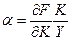 (11)
(11)
Пояснимо цю формулу. Нехай приріст  основних фондів при незмінному другому факторі - трудових ресурсів, відповідає приросту
основних фондів при незмінному другому факторі - трудових ресурсів, відповідає приросту  об’єму випуску. Тоді збільшення об’єму основних фондів
об’єму випуску. Тоді збільшення об’єму основних фондів  відповідає збільшенню випуску на
відповідає збільшенню випуску на  . Отже, при збільшенні об’єму основних фондів на 1%, об’єм випуску збільшиться на
. Отже, при збільшенні об’єму основних фондів на 1%, об’єм випуску збільшиться на 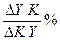 .. Переходячи до границі при
.. Переходячи до границі при 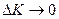 , отримаємо формулу (11).
, отримаємо формулу (11).
Коефіцієнт еластичності по праці
 (12)
(12)
має аналогічний зміст.
Покажемо, що (1) задовольняє умовам виробничих функцій (3) – (6) і визначимо відповідні характеристики для функції Коба-Дугласа.
 ;
;
 ;
;
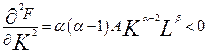 , бо
, бо 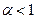 ;
;

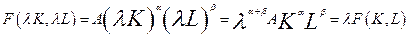
 ,
, 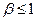
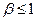 , тому середня продуктивність праці функції Коба-Дугласа є спадною за аргументом
, тому середня продуктивність праці функції Коба-Дугласа є спадною за аргументом 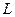 . Тобто зі збільшенням затрат середня продуктивність праці падає. Пояснення: оскільки величина другого фактора К незмінна, то додатково залучена робоча сила не забезпечена додатковими засобами виробництва, що і призводить до зниження продуктивності праці.
. Тобто зі збільшенням затрат середня продуктивність праці падає. Пояснення: оскільки величина другого фактора К незмінна, то додатково залучена робоча сила не забезпечена додатковими засобами виробництва, що і призводить до зниження продуктивності праці.
Аналогічно
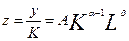 ,
, 
 , тому середня продуктивність праці є спадною;
, тому середня продуктивність праці є спадною;
 , тобто гранична продуктивність праці пропорційна середній продуктивності і завжди менша за неї, бо
, тобто гранична продуктивність праці пропорційна середній продуктивності і завжди менша за неї, бо  , тому
, тому  .
.
Аналогічно

Коефіцієнт еластичності по фондах (капіталовкладення)
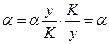 , тобто власне параметр
, тобто власне параметр  у функції Коба-Дугласа і є коефіцієнтом еластичності по фондах, а
у функції Коба-Дугласа і є коефіцієнтом еластичності по фондах, а 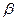 є коефіцієнтом еластичності по праці. Ці коефіцієнти для функції Коба-Дугласа не залежать від величин факторів К та
є коефіцієнтом еластичності по праці. Ці коефіцієнти для функції Коба-Дугласа не залежать від величин факторів К та 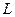 .
.
|
|
|
|
Дата добавления: 2014-01-04; Просмотров: 1801; Нарушение авторских прав?; Мы поможем в написании вашей работы!