Принципи нових методів супутникової геодезії

Успіхи в розробці лазерних далекомірів відкривають можливості вирішення деяких задач астрономії і геодезії шляхом спостереження кутових відбивачів, доставлених на поверхню Місяця. Для спостереження цих відбивачів використовують могутні лазери, сполучені з оптичними телескопами, діаметр яких повинен бути не меншим 1 м, щоб прийняти дуже ослаблений відображений лазерний сигнал. Досягнута в теперішній час точність вимірювань дальності до кутових відбивачів, встановлених на Місяці, становить декілька дециметрів. Однак вже висловлюється надія, що в найближчому майбутньому точність цих вимірювань буде доведена до ±10- 15 см.

Теоретичні питання, пов'язані з можливістю геодезичного використання вимірювань відстаней за допомогою лазера до кутових відбивачів на Місяці, освітлені в роботах дослідників колишнього СРСР і зарубіжних дослідників.

Кожна виміряна відстань ρ від точки М ( обсерваторії) на поверхні Землі до лоцуємої точки А (відбивача) на Місяці є функцією координат цих точок в єдиній системі, наприклад в правій миттєвій зоряній системі координат oxyz, вісь z якій направлена по миттєвій осі обертання Землі до північного полюса

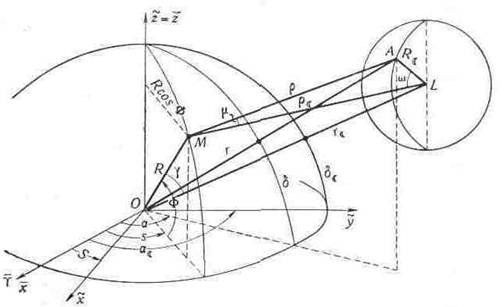
Рис. 7.1. Геометрія лазерної локації Місяця

Світу, вісь х - в істинну точку весняного рівнодення (див. рис. 7.1). Ця система пов'язана через істинний зоряний час S з системою координат Oxyz, вісь z якої співпадає з віссю z, а вісь х направлена в точку початку рахунку довгот.

Рівняння для виміряної відстані ρ зручно виразити через сферичні координати у вигляді

причому

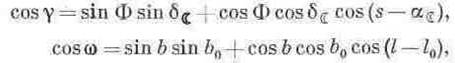
де R, r геоцентричні довжини радіуса-векторів обсерваторії і центра маси Місяця відповідно; Ф -геоцентрична широта обсерваторії М; (s- а)місцевий часовий кут центра маси Місяця в момент спостереження; а, δ геоцентричне пряме піднесення і сходження центра маси Місяця; b, l селеноцентричні широта і довгота лоцуємої точки А; b₀, l₀ - топоцентричні лібрації Місяця по широті і довготі.

Лінеаризуючи рівняння (7.1), прийнявши в ньому за виміряну величину відстань ρ і виразивши інші вхідні в нього величини через шукані параметри, отримаємо рівняння погрішностей для знаходження поправок до прийнятих наближених значень координат обсерваторії, селеноцентричних координат відбивача на Місяці, елементів орбіти Місяця і параметрів фізичної лібрації Місяця. У принципі можна шукати поправки до всіх постійних параметрів, які впливають на рух Землі і Місяці відносно один одного. Але раціональніше шукати поправки до тих величин, які можуть бути знайдені з лазерної локації Місяця з більшою точністю, ніж вони відомі з інших джерел. При цій відстані ρ потрібно вимірювати в такі моменти руху системи Земля - Місяць, коли зміни коефіцієнтів при шуканих поправках максимальні.

Оскільки координати наземних пунктів відомі з високою точністю, то доцільно спочатку уточнити відповідні елементи орбіти, координати відбивача і параметри фізичної лібрації Місяця за декількома певним чином розташованих на його поверхні відбивачах, а потім по отриманих уточнених величинах приступити до уточнення координат обсерваторії. Тут потрібно використати ту обставину, що уточнені на першому етапі величини мало змінюються на коротких інтервалах часу і ці зміни можуть бути обчислені зі значно більшою точністю, ніж абсолютне положення відбивача в геоцентричній системі координат. Маючи на увазі цю обставину, замість (7.1) запишемо наступне вираження (див. рис. 7.1):

де r - геоцентрична довжина радіуса-вектора відбивача, δ, а сходження і пряме піднесення відбивається відповідно, (s - а) місцевий часовий кут відбивача в момент спостереження. В якості величин, що визначаються виберемо радіус R cos Ф паралелі обсерваторії, відстань її від екватора z = z = = R sin Ф і геоцентричну довготу (S- s). Ці величини зручні тим, що вони характеризують положення обсерваторії в геоцентричній системі координат і, разом з тим, в значній мірі незалежні один від одного.

Методику визначення компонентів положення обсерваторії будують таким чином, щоб в рішення входили зміни координат відбивача, а вплив помилок його абсолютних координат, які в деяких випадках можуть бути на один-два порядки більше, були зведені до мінімуму.

На коротких інтервалах часу на досить плавні зміни ρ, викликані переміщенням відбивача в просторі, буде накладатися яскраво виражена періодична складова, зумовлена добовим обертанням обсерваторії навколо земної осі, яка рівна

і пропорційна радіусу паралелі. Ця обставина і дозволяє визначити радіус паралелі обсерваторії.

Знайдений на основі (7.3) радіус паралелі буде залежати від точності прийнятих значень величин r, δ і а. Вимоги до точності геоцентричного радіуса-вектора r невеликі. Помилку прямого сходження а ми можемо вважати постійною протягом нічного сеансу спостережень, оскільки зміни а обчислюються з достатньою точністю. Отже, при симетричних відносно меридіана спостереженнях вплив помилки Δ а компенсується. Найбільшу помилку в радіус паралелі обсерваторії може внести помилка у схиленні відбивача. Однак δ (при аналогічному припущенні постійності його помилки) може бути уточнено по місячному ряду спостережень, оскільки при наявності помилки Δ δ в значенні радіуса паралелі, що визначається буде виявлена складова, пропорційна величині Δ δ sin δ, що має період, рівний періоду обертання Місяця.

З іншого боку, момент, коли зміни в ρ, викликані обертанням Землі, рівні нулю, відповідає проходженню відбивача через миттєвий геоцентричний меридіан обсерваторії. Якщо прийняти, що помилки визначення відстаней рівні ± 2 дм, то цей момент може бути зафіксований з помилкою менше ± 0,5мс. Тоді

s°=а

і

λ=s°-S°,

де s° - момент кульмінації відбивача в шкалі зоряного часу, а S° грінвічський зоряний час в цей же момент.

Шкала зоряного часу, в якій повинен бути зафіксований момент кульмінації відбивача і яка фактично визначає положення початкового меридіана рахунку довгот в системі координат Oxyz, має помилки не менше за 1 мс. З іншого боку, абсолютне пряме сходження а відбивача буде відомо з великою помилкою. Ці обставини не дозволяють визначати геоцентричні довготи обсерваторій з точністю, відповідною точності фіксації моменту кульмінації. Однак при визначенні різниці довгот обсерваторій можна майже повністю виключити помилки шкали зоряного часу і значно ослабити вплив помилок прямих сходжень відбивача, якщо інтервал між спостереженнями з цих обсерваторій буде досить малий.

Визначити z обсерваторії можна безпосередньо з вирішення рівнянь вигляду (7.2) по вимірюванням відстаней при різних схиленнях Місяця (його схилення за півмісяца може змінюватися в межах від 29 до 4-29°). Точність отриманих результатів буде залежати від помилок обчислення приросту r за період порядку півмісяця і від точності знання схилення і буде в декілька разів нижче, ніж точність визначення радіуса паралелі. У такому підході до вирішення задачі важливе те, що при одночасному спостереженні відбивача на Місяці з двох обсерваторій можна в значній мірі звільнитися від вказаних вище помилок і отримати різницю відстаней від площини екватора з такою ж точністю, як і радіуси паралелей обсерваторій. Аналіз точності вирішення перерахованих задач приводить до висновку, що при досягнутій в теперішній час точності лазерної локації Місяця можна чекати, що найближчим часом точність різниці довгот обсерваторій становитиме 1,5 дм, відстані їх від осі обертання Землі до 3 дм, а відстані їх від площини екватора до 1- 2м. Майбуть, передбачувана точність буде досягнута не відразу, а шляхом ряду послідовних наближень, при яких будуть уточнюватися не тільки координати обсерваторії, але і параметри руху Місяця і координати відбивача на її поверхні. Розглянутим методом - лазерною локацією Місяця в подальшому будуть вирішені такі фундаментальні астрономічні і геодезичні проблеми, як: а) визначення коливань миттєвих полюсів Землі з точністю до десятих часток метра, з використанням результатів визначень «миттєвих» радіусів паралелей щонайменше двох обсерваторій, рознесених по довготі приблизно на 90° і розташованих в досить високих широтах (насправді буде потрібне більше їх число, щоб зменшити невизначеність через можливе власного руху обсерваторій); б) створення базису довжиною в декілька тисяч кілометрів (довжина якого може бути визначена з погрішністю ±0,3 - 0,5 м); в) вивчення можливих рухів материків і окремих блоків земної кори.

* * *

Для вирішення деяких наукових задач, що лежать на стику геодезії, астрономії і геофізики, можуть бути використані і спостереження за рухом далеких космічних апаратів (КА), що запускаються до Місяця і планет сонячної системи. Так, високоточне радіотехнічнее стеження за КА, а саме вимірювання відстаней до них і радіальних швидкостей, дозволяє з високою точністю визначати як реальну траєкторію КА, так і її малі відхилення від розрахункової, викликані неточним знанням маси Землі. Це дає можливість уточнити масу Землі М або так звану геоцентричну постійну fM, знання якої в свою чергу спільно з наземними гравіметричними даними дозволяє визначити велику напіввісь загального земного еліпсоїда.

Загальна схема уточнення величини μ = fM за даними стеження за КА наступна. Високоточні радіотехнічні системи ведуть безперервне стеження за КА, визначаючи його дальності і значення радіальної швидкості. По наближених початкових умовах і прийнятому (що уточнюється) значенні μ₀ = = fM₀ виконуює чисельне інтегрування диференціальних рівнянь руху КА. Узгоджуючи методом найменших квадратів обчислені і спостережені величини, проводять одночасне уточнення початкових умов руху і величини μ₀. По суті аналогом цієї задачі є визначення прискорення сили тяжіння методом вільного падіння.

Для з'ясування особливостей методу, що описується, а також вимог до точності вимірювання радіальних швидкостей і дальностей КА розглянемо наступний ідеалізований випадок. Нехай з поверхні сферичної необертаючої Землі вертикально вгору стартує КА. Нехай в точці старту проводяться вимірювання дальностей і радіальних швидкостей КА. Параметр μ пов’язаний з величинами, що вимірюються інтегралом енергії

де r - геоцентрична відстань до КА, r=v - радіальна швидкість КА (в ідеалізованому випадку, що розглядається рівна його повній швидкості), h -постійна енергії, що залежить від початкових умов рушення КА.

Щоб знайти з (7.4) величину μ необхідно виміряти величини r і v, траєкторії, що відносяться до двох точок КА. Тоді на основі (7.4) отримаємо

Звідси можна бачити, що для надійного визначення r необхідно вимірювати відстані і радіальні швидкості КА на початковій дільниці його траєкторії, де зміни цих величин досить великі. Через декілька діб після запуску КА зміни його швидкості стають малими і вимоги до точності її вимірювання сильно зростають. Для оцінки точності вимірювання швидкостей і дальностей КА продиференціюємо (7.5) і, перейшовши до кінцевих приростів, отримаємо

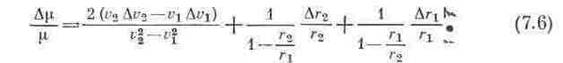
У теперішній час астрономія, геодезія і геофізика зацікавлені в зменшенні помилки визначення геоцентричної постійної μ принаймні до ±0,1 км³/с². Якщо підставити в (7.6) числові значення величин, що вимірюються, взяті за даними стеження за КА «Марінер 9», то прийдемо до висновку, що для визначення величини μ з вказаною точністю необхідно вимірювати радіальну швидкість КА з помилкою всього лише ±0,3 мм/з (при точності вимірювання дальності порядку 30 м). На практиці стеження за КА продовжується безперервно, поки він знаходиться в зоні видимості спостережливих станцій. Тому вказана помилка вимірювання радіальної швидкості КА відноситься до середнього моменту спостережень.

Роботи по уточненню геоцентричної гравітаційної постійної велися в СРСР і в США. Крім того, за даними радіотехнічного стеження за далекими КА вдалося уточнити відношення маси Місяця до маси Землі, а також визначити масу, розміри і стиснення Марса і Венери. У майбутньому ці дослідження отримають подальший розвиток, маючи на увазі необхідність уточнення даних про фігури, розміри і гравітаційні поля тіл Сонячної системи, а також необхідність уточнення деяких фундаментальних постійних астрономії і геодезії.

Зазначимо, що за даними радіотехнічного стеження далеких КА, як і при лазерній локації Місяця, можна визначити радіуси паралелей і різниці довгот станцій стеження. Така можливість вже неодноразово використовувалася, але цей спосіб менш точний в порівнянні з лазерною локацією Місяця.

***

У супутниковій геодезії починають знаходити застосування методи, які своїм походженням зобов'язані прогресу спостережливої космічної техніки. З'ясувалася можливість геодезичного використання радіотелескопів, які в парі утворять радіоінтерферометр. Принцип застосування такої системи в геодезичних цілях полягає в наступному. Випромінювання видаленого точкового радіо джерела приймається на антени радіотелескопів, рознесених на велику відстань, так звану базу інтерферометра. Але випромінювання поступає на ці антени не одночасно, а з деяким відносним тимчасовим запізненням τ, яке зумовлене різницею шляхів радіохвиль від джерела до приймачів. Цю різницю шляхів називають інтервалом запізнення. Через обертання Землі, на поверхні якій знаходяться радіотелескопи, інтервал запізнення буде мінятися з часом в залежності від зміни кута між напрямом бази і напрямом на джерело радіовипромінювання, що спостерігається. Прийняті сигнали з двох обсерваторій передаються на один пункт і там зіставляються. Якщо ці сигнали когерентні, то результуючий сигнал буде мати регулярно повторюючі максимуми і мінімуми в залежності від того, чи укладається в інтервалі запізнення ціле число довжин хвиль, або воно відрізняється від цілого числа на половину хвилі.

Потрібно підкреслити, що на відміну від монохроматичного випромінювання, що дозволяє визначати тільки частоту інтерференційних смуг, досить широка смуга частот, що реєструються радіотелескопами, дозволяє однозначно визначити і час запізнення τ. Точність визначення τ зворотно пропорційна ширині смуги і майже не залежить від довжини бази інтерферометра. Інтервал запізнення і частота інтерференційний смуг сутність функції довжини бази, її напряму і швидкостей обертання Землі, а також координат радіоджерела, що спостерігається.

Якщо точкове джерело випромінювання знаходиться в нескінченності і, отже, передній фронт хвилі плоский, то виміряний час запізнення пов'язаний з параметрами бази наступним співвідношенням:

де τ- виміряний час запізнення, Δ τ несинхронність годин на кінцях бази, θ - кут між напрямом бази і напрямом на джерело радіовипромінювання.

Переходячи до сферичних координат, а це можна зробити, якщо представити cos θ як скалярний добуток одиничних векторів напряму бази і напряму на радіоджерело в геоцентричній системі координат, отримаємо

або

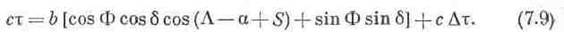
Тут Ф і 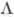кути між базою і площинами відповідно екватора і початкового меридіана, S - гринвічський зоряний час, δ і α- S =γ - суть відповідно cхилення і взятий із зворотним знаком гринвічський часовий кут радіоджерела.

Частота F інтерференційних смуг може бути визначена як добуток середньої частоти f₀ сигналу, що приймається на похідну від τ за часом

або, враховуючи (7. 9),

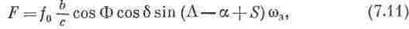
де ω₃ швидкість обертання Землі в радіанах за секунду атомного часу. Частоту F можна розглядати як доплеровський зсув частоти, що приймається, викликаний переміщенням кінців бази відносно джерела випромінювання внаслідок обертання Землі.

Запізнення, що безперервно змінюється можна представити як функцію атомного часу Т, яка буде мати вигляд косинусоїди з амплітудою

зміщеної по осі τ на величину

Тоді запізнення можна представити у вигляді

де

а Δ t=S-ω₃Т- різниця зоряного і перетвореного атомного часу*.

Подібним же чином можуть бути представлені і параметра синусоїди, що відображає зміну частоти F у часі,

Параметри р, q і Δ Т в співвідношеннях (7.14) і (7.16) можуть бути визначені по серії значень τ і F, виміряних на протязі доби, в припущенні, що швидкість обертання Землі за добу не міняється і відома з достатньою точністю. Таке припущення цілком виправдане. Частота f₀ відома з вимірювань.

Таким чином, з обробки спостережень одного радіоджерела ми отримаємо три величини: р, q і Δ Т, які спільно з їх ковариаційною матрицею можна також розглядати як результати вимірювань.

Розглянемо спочатку можливість використання отриманих параметрів р і q. Із-за несинхронності годин ці параметри, отримані по спостереженнях одного радіоджерела, не можуть бути використані для визначення елементів b і Ф бази якщо, навіть вважати, що cхилення джерела нам відоме. Але схилення радіоджерел відомі в цей час з точністю порядку 0,5-1,0," що досить лише для визначення проекції b cos Ф бази із спостережень близьких до екватора об'єктів. Тому, розглядаючи схилення радіоджерела як величину, що визначається, ми будемо в результаті мати чотири невідомих при двох виміряних величинах. Спостереження кожного додаткового радіоджерела буде давати ще одне невідоме і дві виміряні величини. Таким чином, спостереження трьох радіоджерел забезпечить визначення як їх схилень, так і двох елементів бази радіоінтерферометра, а також і несинхронності Δ τ в припущенні, що вона залишається постійною протягом всього періоду спостережень.

Що стосується величин і α, то з структури виразу (7.15) слідує, що вони не визначаються роздільно, а тільки в комбінації ( -α). Направляючий кут бази в площині екватора можна визначити, якщо відоме пряме сходження джерела радіовипромінювання і в припущенні, що S також відоме. Останнє припущення природне, оскільки лише при заданому положенні початкового меридіана, чому в цьому випадку рівнозначне завдання S, можна говорити про величину кута 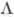. Для визначення величин ( 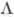-α) необхідно спостерігати принаймні два радіо джерела в досить короткому інтервалі часу (наприклад, на протязі доби), для якого величину Δ t (в (7.15) можна було б вважати постійною при прийнятому значенні швидкості обертання Землі. Ці ж спостереження дають можливість отримати різниці прямих сходжень радіоджерел як різниці величин Δ Т. Для приведення прямих сходжень в зоряну систему координат необхідно принаймні одне з радіоджерел ототожнити з оптично видимою зіркою.

Нарешті, з періодичних спостережень одних і тих же об'єктів може бути визначена зміна величини Δ t, викликана зміною швидкості обертання Землі і неточно прийнятим її значенням. Іншими словами, можуть бути визначені моменти часу в шкалі атомного часу, коли база інтерферометра займає одне і те ж положення відносно радіоджерела. Оскільки шкала атомних годин вкрай рівномірна, то такі спостереження дозволять вивчати нерівномірність обертання Землі.

Радіоінтерферометри стали представляти геодезичний інтерес лише після того, як з'явилися можливості використати радіотелескопи, рознесені на відстані в декілька тисяч кілометрів, як єдину радіотехнічну систему. Цьому сприяло створення високостабільных генераторів частоти (атомні і мазерні годинники), які дозволяють проводити незалежний прийом і запис радіосигналів одного і того ж джерела в різних пунктах і передавати зареєстровані сигнали без фазовий спотворень в одне і те ж місце. Крім того, що генератори частоти використовуються як гетеродини, годинники формують мітки часу, які записуються на магнітних стрічках разом з прийнятими сигналами. Ці мітки дозволяють при звіренні записів радіосигналів, по-перше, відшукати по предобчисленому запізненню сигнали, відповідні одному і тому ж передньому фронту випромінювання, і зіставити їх між собою і, по-друге, виміряти точне значення запізнення. Стабільність годинників при цьому повинна протягом всього сеансу спостережень забезпечувати постійність величини розузгодження їх показань Δ τ в межах точності вимірювання часу запізнення.

Радіоінтерферометри з незалежною реєстрацією сигналів стали вже реальністю. За допомогою їх були проведені спільні радянсько-американські експерименти по вивченню структури радіоджерел. При базі інтерферометра більше за 8000 км був досягнутий кутовий дозвіл 0,0002".

Виконані також і перші геодезичні експерименти. Канадські радіоастроном визначили довжину бази в 2143 км з помилкою по внутрішній збіжності ±20 м. Порівняння з результатами наземних геодезичних вимірювань дало розходження 30 м. Значна частина цього розходження може бути пояснена впливом іоносферної рефракції, оскільки спостереження велися на довжині хвилі 67 см. У США в 1969 р. на радіоінтерферометрі з базою 845 км були виконані дві серії спостережень в дециметровому і сантиметровому діапазонах радіохвиль. Середні квадратичні помилки визначення довжини бази по внутрішній збіжності вийшли по серіях відповідно ±0,5 і ±0,3 м. Отримані значення довжин бази розрізнювалися між собою на 1,3 м і від геодезичного значення відповідно на 2,4 і на 1,1 м.

Основними помилками, що накладають обмеження на можливості геодезичного використання радіоінтерферометрів з великою базою, є помилки, викликані впливом іоносфери і нейтральної атмосфери. Вплив цих помилок зростає із збільшенням довжини бази інтерферометра, оскільки при цьому спостереження доводиться виконувати при малих кутах піднесення. Крім того, обмежується і тривалість спостережень, а отже, і точність висновку по них параметрів інтерференційної картини. З метою підвищення точності результатів плануються нові експерименти з використанням більш коротких довжин хвиль в двох діапазонах (для зменшення і кращого обліку іоносферної рефракції) і розширенням смуги частот, що використовуються.

Для практичної реалізації розглянутого методу необхідно мати мінімум два радіотелескопи діаметром більше за 25 м і два стандарти частоти, що забезпечують її стабільність порядку 1 • 10^-13 за час спостережень. У цьому випадку методом довгобазисної радіоінтерферометрії можуть бути визначені: а) довжина бази з точністю ±0,3- 1,0 м; б) елементи напряму бази з точністю до декількох сотих часток секунди дуги; в) тривалість зоряних діб або швидкість обертання Землі і їх варіації з точністю ±0,001 -0,003s (з двох спостережень на протязі доби). У деяких роботах приводяться очікувані характеристики точності майже на порядок вище вказаних. При цьому попутно можуть бути визначені схилення і різниці прямих сходжень радіоджерел з точністю до сотих часток кутової секунди, а також несинхронності годин з точністю до 1 • 10^-9 сек.

***

Розвиток радіотехнічних методів спостереження за супутниками доплеровського і радіовіддалемірного привело до можливості їх використання для визначення детальних характеристик гравітаційного поля Землі. Ведуться теоретичні дослідження можливостей використання для цієї мети доплеровських вимірювань в системі «супутник-супутник». Аналіз средньоквадратичних значень амплітуд короткоперіодичних збурень в швидкостях і положеннях супутника, виконаних по методу Г. В. Дем’янова, показує, що навіть для низького супутника з висотою орбіти 330 км збудження в положенні не перевищують ±0,1 м на дільниці орбіти довжиною 15°. Отже, якщо вийти з сучасної точності фотографічних і лазерних вимірювань, що забезпечують помилку в положенні супутника порядку ±1 м, то можна прийти до висновку про неможливість використання короткоперіодичних збуреньь ШСЗ для уточнення гравітаційного поля Землі. Середньоквадратичні амплітуди подовжньої складової швидкості ШСЗ на такій же дільниці орбіти для висоти 330 км не перевищують ±0,1 мм/с і для висоти 1000 км - ±0,07 мм/с. Точність же доплеровських вимірювань (з виключенням впливу атмосфери) для систем «супутник-супутник» становить ±0,1- 0,05 мм/с. Звідси слідує, що використання доплеровських вимірювань в системах «супутник-супутник» є єдино можливим методом вивчення тонкої структури гравітаційного поля Землі на основі аналізу короткоперіодичних збурень супутникових орбіт.

Існує два варіанти систем «супутник-супутник», що виключають вплив атмосфери на результати вимірювань. У одному з них мається намір використати два супутники, що обертаються по одній орбіті на невеликій відстані один від одного. У цьому випадку дисперсію різниці їх швидкостей можна прийняти рівній дисперсії збурення подовжньої складаючої швидкості супутника на інтервалі Δ u (різниця їх аргументів широти). У іншому проекті мається намір використати один високий супутник (можливо навіть геостаціонарний, що має період обертання 24^h) і один низький (з висотою приблизно 1000 км). У цьому випадку дисперсія виміряної різниці швидкостей супутників буде практично рівна дисперсії збурень низького супутника, оскільки короткоперіодичні збурення високого супутника близькі до нуля.

Теоретичні дослідження останніх років показали перспективність використання таких засобів вимірювання, як радіоальтиметр (висотомір), встановлений на супутникові. Принцип методу супутникової альтиметрії полягає в тому, що зі супутника з високою точністю вимірюється відстань до найближчої точки океанічної поверхні. При відомій орбіті супутника за результатами цих вимірювань ми можемо визначити фігуру геоїда або, якщо відома фігура геоїда, уточнити орбіту супутника. Звідси витікає принципова можливість вирішення двох важливих задач: а) уточнення супутникових орбіт і б) уточнення прийнятої моделі гравітаційного поля Землі. Результат кожного вимірювання висоти ШСЗ над рівнем моря можна представити як рівняння погрішностей, де невідомими є поправки до початкових умов руху супутника і до коефіцієнтів прийнятої моделі гравітаційного поля Землі, а вільний член цього рівняння рівний різниці виміряної і предобчисленої (за вибраними початковими умовами руху і моделі гравітаційного поля Землі) висот ШСЗ над океанічною поверхнею.

Внаслідок тривалої роботи альтиметра океанічна поверхня, буде покрита сіткою взаємно пересічних профілів. Зрівняна система профілів може служити основою для визначення характеристик фігури геоїда у вигляді схилення прямовисних ліній і висот геоїда над загальним земним еліпсоїдом. Значення висот геоїда, отримані по вимірюваннях супутникового висотоміра, повинні, в принципі, привести до істотного уточнення гравітаційного поля Землі. У разі створення високоточного супутникового висотоміра реально чекати суттєвого уточнення гармонік геопотенціалу високих порядків.

Розвиток нових методів і технічних пристроїв по спостереженню супутників приведе до того, що положення супутників на їх орбітах будуть визначатися з погрішностями, що не перевищують ±1 м. Тим самим супутники з рухомих візирних цілей перетворяться в носіїв високоточних геодезичних координат, тобто в рухомі опорні геодезичні пункти. Тоді отримають широкий розвиток так звані автономні високоточні методи визначення координат точок земної поверхні. У вирішенні цієї задачі істотну роль зіграють доплеровські спостереження за супутниками, що створюють деяку пов'язану систему (подібну навігаційній системі США «Транзит»).

Автономні і інші методи супутникової геодезії дозволять визначати взаємні положення віддалених один від одного точок земної поверхні і створювати високоточні глобальні мережі геодезичних пунктів. Повторні визначення координат цих пунктів через значні проміжки часу дадуть можливість вивчати рухи материків і різні деформації земної кулі за ці проміжки часу. Крім того, по спостереженнях супутників будуть отримані точні дані про рух земних полюсів і особливості обертання Землі біля її осі.

Вивчення різних збурень в русі супутників за результатами високоточних спостережень приведе до отримання більш за точних і докладних даних про гравітаційне поле Землі, так і про фізичну будову навколишнього її простору. Повторні високоточні визначення цих даних через відомі проміжки часу доставлять вельми цінний матеріал для вивчення тимчасових змін гравітаційного поля Землі і різних процесів, що розвиваються в її надрах і в навколоземному просторі.

Дата добавления: 2014-01-04