Згортальні ланцюгові коди

Згортальні ланцюгові (рекурентні) коди уперше були запропоновані відчізняними вченими Фінком Л.М. та Шляпноберским В.І. у 1955 році, і в 1959 році американським вченим Хагельбаргером Д.В.

Ці коди можуть мати різну надлишковість, але найбільш просто вони реалізуються при m = k, тобто коли n = m + k = 2 m = 2 k, а відносна швидкість передачі дорівнює

R = m / k = m /2 m = 0,5.

В цьому випадку операції кодування та декодування створюють послідовно пов’язані ланцюги, що і відображено в одній із назв коду “ ланцюговий ”.

Наприклад, для кожної пари інформаційних символів вихідної послідовності, які є рознесеними між собою на крок додавання (кодування, перемежування) λ, (наприклад, 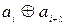, 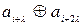) формується один спеціальний перевірочний символ (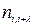,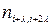). Звернемо увагу на те, що один інформаційний символ використовується для формування двох перевірочних.

На боці приймача із інформаційних символів (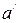) формуються нові перевірочні, які на відміну від перевірочних символів 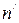, які прийнято, називаються контрольними. Контрольні символи (к) порівнюються із перевірочними і, в разі їх неспівпадання, формується висновок про наявність спотворення. Перевірочні і контрольні символи формуються шляхом складання по модулю 2 інформаційних.

Передавання	Приймання
…	…
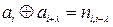
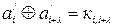
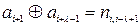
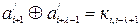
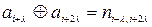
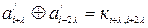
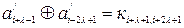
і т.д.

Одна перевірка охвачує ті інформаційні символи, різниця номерів яких дорівнює кроку додавання (глибині перемежування):

і + λ – і = і + λ + 1– (і +1) = і + 2λ + 1– (і +λ + 1) = …= λ.

Кожен контрольний символ порівнюється із відповідним перевірочним:

;

;

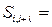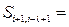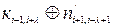і т.д.

Ознакою відсутності спотворень є те, що усі суми дорівнюють нулю:

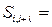
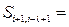…= 0.

Спотвореним може бути як інформаційний, так і перевірочний символ.

На спотворення одного перевірочного символу покаже те, що одна із сум дорівнює одиниці. Наприклад, якщо 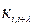не співпадає із 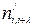, то отримаємо 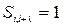, оскільки маємо спотворення в .

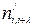Наявність двох сум, які дорівнюють одиниці і віддалені (зсунуті) між собою на крок додавання λ , свідчить про спотворення двох перевірочних символів.

Розглянемо приклад послідовного згортального коду із кроком додавання
λ = 3 при умові, що перевірочні символи прийнято без спотворень. Нехай із спотворенням прийнято три інформаційних символи. Формування перевірочних і контрольних символів показано на рис. 1.

( Увага! Розташування перевірочних символів на цьому рисунку показано умовно і не відповідає вимогам до нього!)

Рис. 1. Формування перевірочних і контрольних символів при наявності спотворення в символах з номерами 4, 5, 6

Порівняємо контрольні елементи із перевірочними, які є прийнятими:

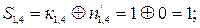
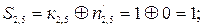
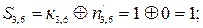
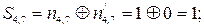
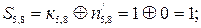
Видно, що утворилися три пари сум, які дорівнюють одиниці і зсунуті на крок додавання λ = 3:

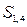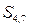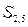і 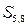; 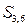і ; і .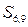

Оскільки один інформаційний символ використовується для формування двох перевірочних, які є рознесеними між собою на крок додавання λ, (наприклад, 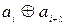, 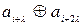) робимо висновок, що спотворені ті інформаційні символи, номери позицій яких є спільними в кожній парі сум, тобто 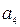, , 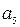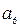. Значення цих символів необхідно виправити на протилежні: прийнято 0 – повинна бути 1 і навпаки. Таким чином, виправлено три спотворення, тобто кількість спотворень, що виправляються, дорівнює кроку додавання. Значення цих символів необхідно виправити на протилежні: прийнято 0 – повинна бути 1 і навпаки. Таким чином, виправлено три спотворення, тобто кількість спотворень, що виправляються, дорівнює кроку додавання.

Із цього прикладу можна зробити і побічний висновок: значення λ визначає не лише крок додавання, а і глибину перемежування, тобто кількість окремих незалежних ланцюгів коду. Дійсно, при λ = 3 маємо три незалежних ланцюги:

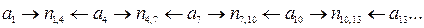
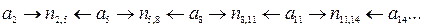
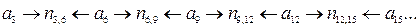
Розглянемо ще один приклад. Значення інформаційних і перевірочних символів при передаванні – такі ж як і в попередньому прикладі (див. рис. 1). Перевірочні символи прийнято без спотворень, із спотвореннями прийнято інформаційні символи 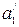,,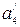 , , 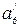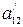(рис. 2).

Результат порівняння контрольних і перевірочних символів покажемо для кожного із ланцюгів:

перший ланцюг: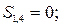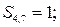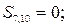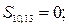
другий ланцюг: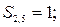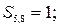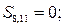
третій ланцюг: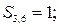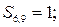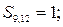

Рис. 2. Формування перевірочних і контрольних символів при наявності спотворення в символах з номерами 1, 4, 5, 6, 12

Із отриманих результатів додавання контрольних і перевірочних символів розглянемо можливість виправлення спотворень в кожному незалежному ланцюзі коду.

Результат порівняння контрольних і перевірочних символів покажемо для кожного із ланцюгів. Перший ланцюг включає 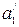,,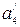 , , 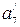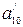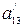та відповідні перевірочні символи 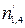,,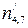 , 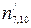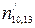. За умовою спотвореними є 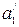,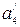. В цьому ланцюзі

перший ланцюг: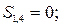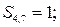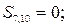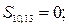

тільки одна із сум дорівнює одиниці:

.

Виходячи із правил виявлення спотворень, можна стверджувати, що спотвореним є перевірочний символ 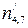. Однак це суперечить умові прикладу: перевірочні символи прийнято без спотворень. Тобто, виявлення спотворених інформаційних символів, які входять до першого ланцюга, не здійснено. Більш того, невірно буде “виправленим” перевірочний символ .

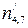Другий ланцюг включає 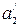,, , 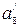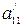та 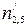,,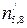 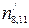. За умовою спотворено .

другий ланцюг: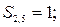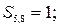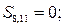

Те, що в цьому ланцюзі дорівнюють одиниці дві суми (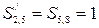), свідчить, що спотвореним є один інформаційний символ із спільним для цих сум індексом, тобто . В другому ланцюзі спотворення буде виправлено вірно.

У третій ланцюг входять 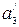,,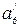 , 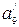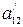та 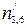,,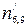 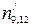. Згідно із умовою прикладу спотвореними є 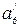та .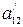

третій ланцюг: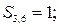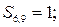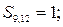

тобто, у цьому ланцюзі три суми дорівнюють одиниці

.

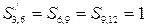За рівнянням 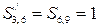можна виправити 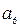; рівняння 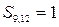вказує на спотворення 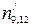, що суперечить умові. Таким чином, спотворення 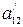не виявлено і невірно виправлено 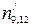. Якщо узяти 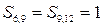, можна вважати спотвореним 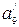, що є також невірним.

Розглянувши два приклади із різною кількістю спотворених інформаційних символів, можна зробити наступні висновки про те, що:

1. В разі, коли спотворення перевищує можливості коду, код не лише не здатен виявляти та виправляти спотворення, але і вносить додаткові спотворення:

2. Інформаційні символі одного ланцюга розташовуються на відстані λ інформаційних та λ перевірочних, отже на відстані 2 λ символів один від іншого;

3. Місце розташування перевірочних символів визначається двома обставинами: по-перше, групова завада не повинна одночасно охвачувати інформаційні і відповідні перевірочні символи; по-друге, не повинно бути неправильного виправлення інформаційних символів.

Із цих міркувань перевірочні символи розташовуються на відстані 2 λ + 1 символів від найближчого свого інформаційного. Наприклад, перевірочний символ 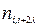, створений із інформаційних 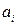та 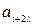повинен займати [(i + 2λ) + 2 λ + 1 ] = (і + 4 λ + 1) позицію.

При цих умовах згортальний код виправляє групове спотворення із λ інформаційних символів (див. перший приклад).

Розглянемо приклад формування номерів символів інформаційної послідовності для кроку додавання λ = 2.

Із викладеного раніше зрозуміло, що:

1. Інформаційні та перевірочні символи повинні чергуватися. Для визначеності будемо вважати, що інформаційні символи мають непарні номери, а перевірочні – парні;

2. Повинні бути сформованими два (λ = 2) незалежних ланцюги формування перевірочних (а в подальшому і контрольних) символів.

В таблиці 1 наведено розподіл номерів символів послідовності між інформаційними та перевірочними (контрольними) та розподіл номерів інформаційних символів між ланцюгами.

Таблиця 1

Номери символів інформацій-ної послідовнос-ті

Номери інформацій-них символів першого ланцюгу

Номери інформацій-них символів другого ланцюгу

Номери перевірочних символів

Взаємне розташування інформаційних і перевірочних символів для наведеного прикладу представлено на рис. 3.

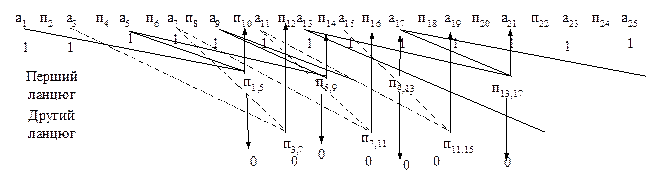Рис. 3. Взаємне розташування інформаційних і перевірочних символів при
λ = 2

Оскільки рознесення між інформаційними символами кожного незалежного ланцюга складає λ інформаційних символів, то і відстань між відповідними перевірочними символами також дорівнює кроку додавання.

Важливою характеристикою згортального коду є мінімально допустима відстань між суміжними груповими спотвореннями, коли ще є можливим виправлення спотворень (див. рис. 4). Ця відстань повинна забезпечувати правильне приймання 2 λ інформаційних символів після спотворення та 2 λ перевірочних, які охвачують спотворені інформаційні символи. Тому мінімальна допустима відстань дорівнює 4 λ + 1 символів.

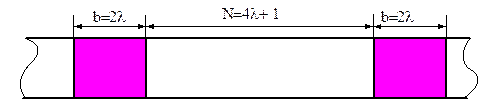
Рис. 4. Мінімально допустима відстань між груповими спотвореннями

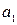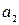Оскільки в інформаційних повідомленнях, що передаються безперервно, перевірочні та інформаційні символи чергуються: , п, , п, 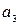, …, то це означає, що інформаційні символи, що входять у одну перевірку, рознесені проміж собою на λ інформаційних і λ перевірочних символів. Тобто, при кроці додавання λ інформаційних символів згортальний код виправляє групове спотворення із b = 2 λ інформаційних і перевірочних символів, а мінімально допустима відстань між груповими спотвореннями дорівнює

М = 4 λ +1 = 2 b + 1

інформаційних і перевірочних символів.

Дата добавления: 2014-01-04