Использование этих гидромеханических моделей и свойств жидкостей позволяет решить основные задачи гидромеханики в бурении

КИНЕМАТИКА СПЛОШНОЙ СРЕДЫ

Задача кинематики - описание движения среды независимо от внешних условий, которые инициируют и поддерживают движение. Т.к. СС представляет собой непрерывную совокупность точек, то чтобы описать её движение, необходимо описать движение ВСЕХ точек.

Движение обычно определяется по отношению к некоторой системе отсчёта, которую мы называем системой координат. Если нет особой оговорки, то через х₁, х₂, х₃ будем обозначать координаты любой ортогональной системы.

Способ Лагранжа. Задаются законы изменения положения (подвижная система отсчёта), скорости, ускорения и других величин, то есть кинематические уравнения движения:

х_i = x_i (x₁,x₂,x₃, t) (i = 1,2,3), (1.1)

где x_i являются координатами фиксированной (индивидуальной) точки среды. Совокупность величин x и t называются переменными Лагранжа.

Построение математической модели любой СС опирается на понятие закона движения.

Запишем проекции скоростей и ускорений точек среды на оси координат х_i, которые определяются обычными равенствами:

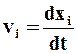, (1.2)

Способ Эйлера. Задаются перемещение, скорость, ускорение в точке пространства (неподвижная система отсчёта), мимо которой в данный момент проходят частицы среды, как функции координат точек пространства x_i и времени t:

u_i = u_i (x₁, x₂, x₃ , t);

v_i = v_i (x₁, x₂, x₃ , t); (1.3)

a_i = a_i (x₁, x₂, x₃ , t).

Совокупность параметров х_i и t называют переменными Эйлера.

Переход от переменных Лагранжа к переменным Эйлера и наоборот. Если у нас есть закон движения СС в форме (1.1), то чтобы перейти к переменным Эйлера необходимо разрешить уравнения (1.1) относительно x_i.

x_i = x_i(x₁, x₂, x₃ , t). (1.4)

При фиксированных координатах х_i эти соотношения указывают те точки x_i СС, которые в разные моменты времени проходят через данную точку пространства.

Для перехода от переменных Лагранжа к переменным Эйлера (х_i, t), необходимо в формулы для проекций скоростей v_i = v_i (x₁,x₂,x₃, t) и других величин подставить соотношения (1.4).

Пусть задано распределение скорости в форме Эйлера (1.3), тогда, учитывая равенства (1.2), получим СИСТЕМУ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ относительно х_i:

где (i = 1,2,3)

Решая эту систему, определим х_i = х_i(С₁, С₂, С₃, t), где - С₁, С₂, С₃ -постоянные, определяемые по х_i при t = t₀, то есть, они являются координатами индивидуальной точки сплошной среды (переменными Лагранжа).

ПОЛЯ В ГИДРОДИНАМИКЕ

При изучении движения жидкости рассматривают её как сплошную среду. Таким образом, рассматривают не движение конечного числа отдельных частиц, а поля различных физических величин: скорости, плотности, давления и т.д. Такие поля можно назвать материальными полями. Математически эти поля описывают системой функций от координат и времени. Такой подход типичен не только для механики сплошных сред, но и для ряда других областей физики.

В общем случае поле является пространственным (трёхмерным), однако, иногда задачу упрощают, и рассматривают двумерные (плоские) или одномерные поля. В этом случае полагают, что физические величины зависят от одной или двух пространственных координат.

Если физические величины не зависят от времени, то поле называют стационарным, в противоположном случае - нестационарным.

При математическом описании полей предполагают, что существуют пределы значений физических величин в точке. Такой подход упрощает физическую реальность, так как не учитывает дискретность строения материи, но такая абстракция оправдана, нужно только разумно ограничивать область полученных результатов.

Так как в практических задачах размеры обтекаемых тел намного порядков больше молекулярных размеров, то в этих задачах жидкость можно рассматривать как сплошную среду.

СКАЛЯРНЫМ называют поле, которое характеризуют в каждой точке пространства одним числом. Скалярное поле описывают одной функцией, зависящей от трёх координат. (Например, поле плотности или температуры).

Основное свойство скалярной функции а(х₁,х₂,х₃) состоит в том, что её численное значение не меняется при преобразовании координат. Если перейти от старой х₁,х₂,х₃ к новой х^¢₁,х^¢₂,х^¢₃ системе координат, то значения плотности или температуры в фиксированной точке пространства, естественно, не изменяются:

а(х^¢₁,х^¢₂,х^¢₃)= а(х₁,х₂,х₃).

ВЕКТОРНЫМ называют поле, которое в каждой точке пространства характеризуют ВЕЛИЧИНОЙ и НАПРАВЛЕНИЕМ. Например, поле скоростей жидкости. Вектор а в пространстве трёх измерений может быть задан тремя компонентами:

а₁(х₁,х₂,х₃), а₂(х₁,х₂,х₃), а₃(х₁,х₂,х₃),

то есть, тремя функциями от трёх переменных. Это можно записать в виде матрицы-столбца:

а ÜÞ

Введём новую декартову систему координат с тем же началом, НО С ДРУГИМ НАПРАВЛЕНИЕМ ОСЕЙ. Пусть l _ij - направляющий косинус оси x^¢_j относительно оси x_i (i = 1,2,3; j = 1,2,3). Вычислим проекции того же вектора на новые оси координат:

a^¢₁ = l ₁₁ a₁ + l ₂₁ a₂ + l_{3 1} a₃;

a^¢₂ = l ₂₁ a₁ + l ₂₂ a₂ + l₂₃ a₃;

a^¢₃ = l ₃₁ a₁ + l ₃₂ a₂ + l₃₃ a₃;

Следовательно, вектор подчиняется определённому закону преобразования его компонент и отличается от скалярной величины, численное значение которой не меняется при преобразовании координат. То есть, сам вектор не меняется в новых координатах, а меняются его компоненты.

Это выражение можно представить в индексной форме записи в виде суммы:

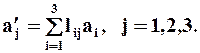
Или ещё более короткой

При такой записи пользуются двумя правилами:

1. Соглашение о суммировании. По индексу, встречающемуся дважды (немой индекс), производят суммирование от 1 до 3.

2. Соглашение о ранге. Индекс, встречающийся один раз (свободный индекс), пробегает значения от 1 до 3.

Таким образом, уравнение с одним свободным индексом означает запись трёх уравнений.

Помимо скалярных и векторных полей в МСС рассматриваются ещё и ТЕНЗОРНЫЕ ПОЛЯ.

Рис.1.1 Система напряжений на гранях элементарного объёма (Г.С. Самойлович. Гидрогазодинамика.С.8).

Вырежем в жидкости элементарный параллелепипед с рёбрами dx₁, dx₂, dx₃ (рис.1.1). На грани этого параллелепипеда со стороны остальной жидкости действуют поверхностные напряжения. В общем случае на каждую грань действуют как НОРМАЛЬНЫЕ так и КАСАТЕЛЬНЫЕ напряжения. В принятой записи каждое из напряжений будет иметь два индекса. Первый индекс означает ориентацию площадки, на которую действует напряжение, второй - ось проектирования.

Компоненты напряжений можно записать в виде матрицы тензора напряжений

при i = 1,2,3; j = 1,2,3.

Первый индекс означает номер строки, второй - номер столбца. Нормальные напряжения имеют два одинаковых индекса - диагональ матрицы. Касательные напряжения имеют разные индексы. Ранг тензора равен числу индексов компонент.

Тензор второго ранга описывается в общем случае девятью функциями трёх переменных. Однако этот тензор обладает важной особенностью. Из условия равенства нулю моментов, действующих на элементарный объём следует, что касательные напряжения с одинаковыми, но расположенными в обратном порядке индексами равны: s_ij = s_ji. Такой вектор называется симметричным и может быть записан как:

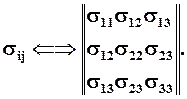
Следовательно, такой тензор напряжений выражается через шесть функций трёх переменных.

Компоненты напряжений представляют как нормальные, так и касательные напряжения. КАСАТЕЛЬНЫЕ НАПРЯЖЕНИЯ ВОЗНИКАЮТ ВСЛЕДСТВИЕ ВЯЗКОСТИ, которой обладают все реальные жидкости. В покоящейся вязкой жидкости касательные напряжения отсутствуют, так как скорости деформации равны нулю, а нормальные напряжения вызваны только давлением и не зависят от ориентации площадки. (Закон Паскаля).

Идеальная жидкость это жидкость, лишённая вязкости. Следовательно, в идеальной жидкости касательные напряжения отсутствуют, и матрица тензора напряжений принимает вид:

.

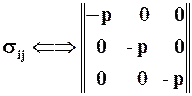Перед Р по условию поставлен знак - минус, так как давление обычно сжимает жидкость, то есть действует против положительного направления нормали к площадке.

Матрицу (1.10) можно сокращённо записать в виде s_ij = - P d_ij,

где d_ij = 1 при i = j; d_ij = 0 при i ¹ j, СИМВОЛ КРОНЕКЕРА.

Понятие установившегося движения относительно, так как в зависимости от выбранной системы координат одно и то же движение может быть установившимся и неустановившимся.

Пусть распределение плотности задано в переменных Лагранжа:

r = r (x₁,x₂,x₃, t), тогда изменение плотности частицы СС равно .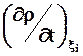

Если функция задана в переменных Эйлера: r = r (x₁, x₂, x₃, t), необходимо перейти к переменным Лагранжа и воспользоваться правилом дифференцирования сложной функции, в результате чего получим:

Производная 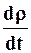называется полной производной (индивидуальной, субстанциональной)и характеризует изменение плотности данной частицы сплошной среды в единицу времени.

Производная 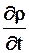называется частной (местной, локальной) и характеризует изменение плотности в данной точке пространства в единицу времени.

Величина называется конвективной производной.

Аналогично формуле (1.5) можно написать формулы для определения полной производной по времени проекций любой векторной величины, заданной в переменных Эйлера.

Для любого векторного поля используют понятие векторных линий. Векторные линии - это семейство линий, касательные к которым совпадают с направлением вектора. В случае поля скоростей эти линии принято называть ЛИНИЯМИ ТОКА.

Если выбрать произвольную кривую С, не совпадающую с линией тока, и через каждую её точку провести линию тока, то образуется ПОВЕРХНОСТЬ ТОКА. Если кривая С замкнута, поверхность тока превращается в ТРУБКУ ТОКА.

Аналитически семейство линий тока можно найти из условия коллинеарности (расположения на одной прямой или на параллельных) элемента 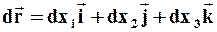, взятого вдоль линий тока, и вектора скорости 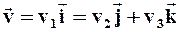, то есть . Где dl - скалярный параметр.

Запишем дифференциальные уравнения линий тока в проекциях:

(i = 1,2,3).

Здесь - величина t - параметр.

Уравнения, описывающие закон движения или траектории движения частиц сплошной среды будут выглядеть таким образом, где t - переменная величина:

(i = 1,2,3).

То есть, линии тока не совпадают с траекториями. Совпадать они могут только в двух случаях:

1. При установившихся движениях (тогда между двумя последними уравнениями нет различия);

2. При неустановившихся течениях (когда поле скоростей меняется по величине, но не меняется по направлению).

Если какая-либо скалярная величина задана как функция переменных Эйлера, то в каждый момент времени можно рассматривать поверхность, где

f (x₁, x₂ , x₃ ,t) = const,

которая называется поверхностью равного уровня или эквипотенциальной.

Вектор-градиент скалярной функции r в точке М – это вектор, направленный по нормали 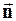в какой-либо точке М поверхности (1.9) в сторону роста r и равный по величине .

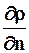Вектор-градиент обозначается как grad r и вычисляется по формуле:

,

где 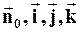- единичные векторы по направлению 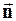и вдоль координатных осей.

Проекция вектора grad r на некоторое направление определяет изменение плотностей в этом направлении:

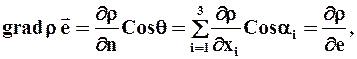
где q - угол между направлениям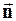и и ; Cos a_I – направляющие косинусы вектора .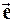

Наибольшее изменение плотности происходит в направлении, нормальном к поверхности (1.9).

Поток скорости через поверхность. Если в поле скорости V (или любой другой векторной величины) мысленно провести некоторую поверхность S и в каждой точке её задать нормаль 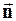, то для определения объёма жидкости, протекающей за единицу времени сквозь поверхность S, необходимо вычислить интеграл

.

Поток скорости сквозь замкнутую поверхность S, отнесённый к единице объёма V, заключённого внутри S, называется РАСХОЖДЕНИЕМ или ДИВЕРГЕНЦИЕЙ скорости, т.е.

.

В декартовой системе координат дивергенция скорости вычисляется по формуле:

.

Отсюда видно, что дивергенция скорости определяет скорость объёмного расширения жидкости в бесконечно малой окрестности данной точки. Поэтому поток скорости через замкнутую поверхность S должен быть равен расширению всего объёма V жидкости внутри S, то есть

Дата добавления: 2014-01-04