Максимальная скорость потока, то есть скорость ядра, определяется по формуле

,

а объёмный расход вычисляется по формуле Букингема

,

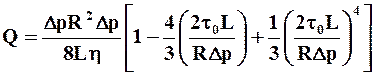соответственно

Если вместе с выражением для средней скорости воспользоваться формулой Дарси-Вейсбаха, то получим для безразмерного коэффициента сопротивления выражение:

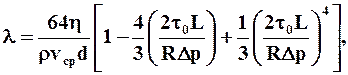
откуда видно, что l невозможно определить, не зная значение Dр.

В общем случае значение для вязкопластичной жидкости может определяться по формуле:

,

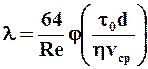где t₀d/hv_ср = Sen - безразмерный параметр, называемый критерием Сен-Венана-Ильюшина, характеризующий эффект пластичности жидкости. Вид функции j аналитически определить затруднительно, но для практических расчётов можно использовать формулу, дающую незначительную погрешность в области малых скоростей сдвига:

,

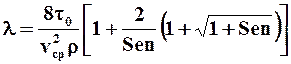ОБРАТИТЕ ВНИМАНИЕ, что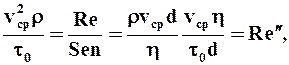

где безразмерная величина Re¢¢ представляет собой ОТНОШЕНИЕ СИЛ ИНЕРЦИИ К СИЛАМ ПЛАСТИЧНОСТИ.

Для определения значения l по значениям чисел Рейнольдса и Сен-Венана - Ильюшина существуют НОМОГРАММЫ.

Для упрощенных расчётов (для целей бурения) величину l можно определять по формуле l = 64 Re ^*:

где Re^* - обобщённый параметр Рейнольдса, который в этом случае не является критерием для оценки вида течения (для этих целей в данном случае необходимо знать параметр Сен-Венана):

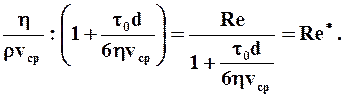
15. Формулы для определения коэффициента сопротивления при различных условиях течения.

ü турбулентный режим течения (круглая цилиндрическая труба), Re = 2500 - 7000: (формула Блазиуса)

;

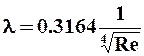ü глинистые и цементные растворы Re = 2500 - 40 000 (формула Мительмана Б.И.):

;

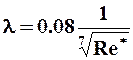ü глинистые и цементные растворы Re = 2500 - 50 000 (формула Шищенко Р.И., Ибатулова К.А.):

,

при значениях Re > 50 000 коэффициент сопротивления может быть принят постоянным и равным 0.02.

ü ламинарное течение в трубах аномально вязких систем (псевдопластичные жидкости) ф. У. Уилкинсона:

где Re¢ - обобщённый критерий Рейнольдса для псевдопластичных жидкостей; k и n - показатели консистенции и степени для псевдопластичных жидкостей.

ü турбулентный режим течения вязкопластичных жидкостей в трубах (аппроксимационная формула Доджа и Метцнера): , где а и - безразмерные коэффициенты, определяемые в зависимости от (см. Басарыгин Ю.М., Будников В.Ф., Булатов А.И. Теория и практика предупреждений осложнений и ремонта скважин при их строительстве и эксплуатации. стр. 106).

ü течение вязкой несжимаемой жидкости в цилиндрическом коаксиальном канале. (Там же).

16. ТЕОРИЯ ПОДОБИЯ. Для решения ряда гидромеханических задач не удаётся найти аналитического решения, тогда прибегают к экспериментальным методам исследования, обобщая частные случаи на большой класс схожих задач. Для осуществления такого перехода пользуются различными критериями подобия.

ü геометрическое подобие. Два цилиндрических круглых трубопровода будут геометрически подобны, если все размеры одного могут быть получены умножением всех размеров имеющегося тела на некоторый постоянный коэффициент.

ü кинематическое подобие. Если два потока жидкости имеют геометрически сходственные ограничивающие поверхности и скорости в сходственных точках будут пропорциональны, то такие потоки кинематически подобны.

ü динамические подобие. Если для геометрически подобных потоков жидкостей на сходственные элементы действуют пропорциональные силы, то говорят о динамическом подобии.

Наиболее общий подход при использовании теории подобия - анализ дифференциальных уравнений движения, позволяющий определить КРИТЕРИИ ПОДОБИЯ ОБЪЕКТОВ.

Рассмотрим одномерное уравнение Навье-Стокса для подобных объектов 1 и 2:

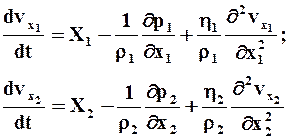
то для выполнения условий подобия явлений необходимо обеспечить следующее: x₁ = m_Lx₂; v_x1= m_vv_x2; h= m _hh₂; p₁ = m_pp₂; X₁ = m_QX₂; r₁ = m_r r₂,

где m_L,m_v, m _h, m_p, m_Q, m_r -соответственно масштабы подобия длин, скоростей, вязкостей, давлений, сил тяжести, плотности.

Подставляя последние выражения в уравнение Навье-Стокса для объекта 1 и принимая во внимание, что m_t =m_L /m _v получаем:

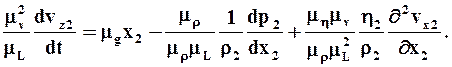
Для того, чтобы явления для объектов 1 и 2 были одинаковыми, необходимо равенство всех коэффициентов для всех членов (тогда уравнение для объекта 1 переходит в уравнение для объекта 2), т.е.

Из полученного условия можно составить три независимых гидромеханических критерия подобия:

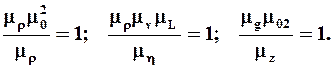
Согласно первому критерию, который называется коэффициентом Эйлера или коэффициентом давления, имеем

согласно второму - критерию Рейнольдса , и третьему - критерию Фруда

Следовательно, для полного гидромеханического подобия ламинарного течения вязкой несжимаемой жидкости необходимо равенство Re, Fr, Eu.

В отдельных задачах возможно равенство некоторых критериев. Так, для определения потерь давления в горизонтальной круглой цилиндрической трубе ранее была показана необходимость равенства лишь критерия Рейнольдса, что соответствует одинаковому значению коэффициента сопротивления l.

ОБРАТИТЕ ВНИМАНИЕ, что критерий Re является отношением сил инерции к силам трения; критерий Fr - сил инерции к силам тяжести, Eu - перепада давления к силам инерции.

Из приведённых критериев можно получить ещё три критерия: - число Стокса, число Лагранжа и гидравлический уклон соответственно.

Все остальные сочетания из соотношений сил инерции, тяжести, трения и перепада давления будут обраными величинами приведённых шести критериев.

Для вязкопластичных жидкостей помимо приведённых критериев подобия имеются условия динамического подобия, обусловленные наличием сил пластичности.

Ø Отношение сил пластичности к силам вязкости характеризует критерий Сен-Венана-Ильюшина ;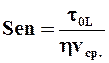

Ø Сил тяжести к силам пластичности - критерий Стокса ;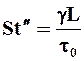

Ø Перепада давления к силам пластичности

УРАВНЕНИЯ ДВИЖЕНИЯ И РАВНОВЕСИЯ

Основным динамическим уравнением движения материальной точки является 2-й закон Ньютона m`a = `F, а широко используемым следствием этого закона являются следующие общие теоремы движения системы материальных точек:

Ø производная по времени от количества движения 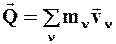равна сумме всех действующих на систему внешних сил (1.45) и называется уравнением количества движения, или уравнением импульсов:

Ø производная по времени от кинетического момента системы относительно какого-либо неподвижного центра О равна сумме моментов 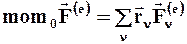всех внешних сил, действующих на систему, относительно того же центра, т.е. (1.46) называется уравнением моментов количества движения;

Ø дифференциал кинетической энергии системы равен сумме элементарных работ 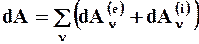всех действующих на систему внешних и внутренних сил, т.е.(1.47) называется уравнением механической энергии или теоремой живых сил.

Для любого мысленно выделяемого индивидуального объёма сплошной среды, ограниченного поверхеностью, уравнения (1.45-1.47) действительны, если динамические величины определить следующим образом:

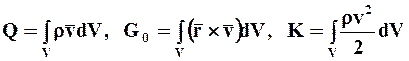
(соответственно количество движения, момент количества движения и кинетическая энергия сплошной среды в объёме V);

(соответственно сумма внешних объёмных и поверхностных сил и их моментов относительно некоторого неподвижного центра О, действующих на среду в объёме V). Силы и их моменты непрерывно определены и сосредоточены.

Сумма элементарных работ внешних и внутренних объёмных и поверхностных сил

.

В этом случае уравнения (1.45) и (1.46) являются основными постулируемыми динамическими соотношениями МСС. Они служат исходными для описания любых движений СС, в том числе разрывных движения и ударных процессов.

Уравнение (1.47) одно из наиболее важных следствий уравнений (1.45) и (1.46) при непрерывных движениях в пространстве и времени.

При непрерывных движениях интегральная теорема движения (1.45) эквивалентна следующим 3 дифференциальным уравнениям:

в декартовой системе координат:

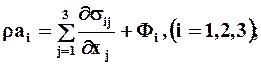
в цилиндрической системе координат при осевой симметрии

где проекции ускорения вычисляют по формулам (1.9).

Эти уравнения, связывающие компоненты v_i вектора скорости и тензора напряжений являются основной системой дифференциальных уравнений движения для любой СС, представляющих собой уравнение баланса количества движения (импульса) для бесконечно малого объёма среды.

Если движения частиц происходят без ускорения (= 0) или они пренебрежимо малы, то уравнения (1.48) называются дифференциальными уравнениями равновесия.

При непрерывном движении сплошной среды теорема моментов количества движения (1.46) в дифференциальной форме сводится к выводу о том, что тензор напряжений симметричен, т.е. s = s. Если тензор напряжений симметричен, то уравнения моментов количества движения удовлетворяются тождественно.

Интегральная теорема живых сил (1.47) эквивалентна следующему дифференциальному уравнению:

dK = dW = dA^(e) (1.49)

где:

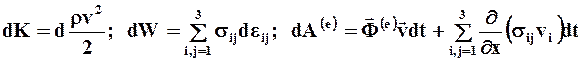
соответственно изменение кинетической и потенциальной энергии бесконечно малого объёма сплошной среды, элементарная работа внешних объёмных и поверхностных сил, действующих на бесконечно малый элемент объёма среды.

Уравнение (1.49) является следствием уравнения движения (1.48) и представляет собой УРАВНЕНИЕ БАЛАНСА МЕХАНИЧЕСКОЙ ЭНЕРГИИ.

В общем случае оно не является законом сохранения энергии, но его можно так трактовать тогда, когда механическая энергия тела не переходит в тепловую или другие виды энергии. Общий закон сохранения энергии в этом случае распадается на два: закон сохранения механической энергии и закон сохранения энергии другого вида.

ДВИЖЕНИЕ ЖИДКОСТЕЙ И ГАЗОВ В ПЛАСТАХ

Заканчивание скважин стр. 64 –69

При рассмотрении движения жидкостей и газов в пластах, представляющих собой проницаемую среду, необходимо знать характер изменения давления в точках пласта и на его границах, а особенно на стенках скважины, а также расход пластовых флюидов через какие-либо ограничивающие поверхности.

При бурении это представляет интерес с позиций оценки процессов газоводонефтепроявлений, поглощений, проникновения бурового раствора и продуктивные пласты, ухудшения проницаемости призабойной зоны и др.

Дата добавления: 2014-01-04