Открытые марковские сети

Открытые - в смысле поступления требований извне и ухода их из сети

N узлов, в каждом приборов (показательного обслуживания)

Структура i -го узла

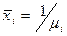секунд - среднее время

- внешний пуассоновский источник с интенсивностью требований/с

- вероятность поступления требования из узла i в узел j

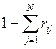- вероятность покидания сети

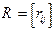- матрица

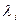интенсивность поступления требований в i -й узел

В сетях с петлями процессы поступления требований в разные узлы не являются пуассоновскими. Однако удивительный факт, известный как теорема Джексона, утверждает, что каждый узел ведет себя так, как если бы его вход был пуассоновским. Если 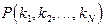- стационарная вероятность того, что в i -м узле находится требований (i= 1,2,... N), то при для всех i согласно этой теореме

(теорема декомпозиции для открытых марковских сетей - теорема Джексона)

- стационарная вероятность того, что требований находятся в системе 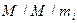при интенсивности входящего потока 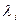и среднем времени обслуживания

Задача Клейнрока

Сеть с коммутацией сообщений (пакетов) имеет N узлов и M каналов. Каналы бесшумные и абсолютно надежные, пропускная способность i-го канала 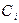бит/с. Все i узлов соответствуют узлам коммутации сообщений (пакетов), абсолютно надежны, выполняют сборку/разборку сообщений, выбор маршрутов, хранение в буферах (протоколы 1,2,3 уровней). Модель учитывает очереди к каналам и время передачи пакета по каналам. Время обработки пакета в узле пока не учитывается.

Трафик поступающих в сеть пакетов от внешних источников образует пуассоновский процесс со средним 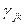- пакет, приходящий в узел i и предназначенный для узла k.

Полный внешний трафик, поступающий в сеть и покидающий ее определим как

Длины всех пакетов независимы и распределены по показательному закону со средним значением бит. Для размещения этих пакетов в узлах сети имеется память неограниченной емкости. Используется процедура фиксированного выбора маршрутов. Это означает, что для данной пары источник-адресат в сети имеется только один путь.

Поскольку каждый канал в сети рассматривается как отдельный обслуживающий прибор, обозначим через 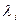среднее число пакетов в секунду, проходящих по i -му каналу. Полный трафик в сети:

Стоимость построения (капитальные затраты) i -го канала с пропускной способностью 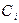задается функцией стоимости , зависящей от номера и пропускной способности канала. Стоимость всей сети (стоимость узлов включается в стоимость каналов связи)

Определим задержку в сети как полное время, которое пакет проводит в сети. Будем говорить о средней задержке пакета в сети T.

Обозначим через 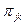путь, по которому идут пакеты, возникающие в узле j и имеющие в качестве узла назначения узел k. i -ый канал с пропускной способностью 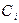включен в путь 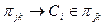, если пакеты, идущие по этому пути, проходят этот канал. Поэтому:

Обозначим - среднее время задержки пакета в канале i, включая среднее время ожидания в очереди к i -му каналу и среднее время передачи пакета со средней длиной бит по каналу со скоростью бит/с -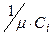

Для системы M/M/1, описывающей канал

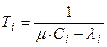
Применяя формулу Литтла для всей сети, имеем: среднее число пакетов в сети равно 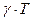. Среднее число пакетов, ожидающих или использующих i-ый канал, равно 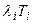Тогда

- вогнутая функция

если сеть не нагружена, т. е. и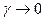

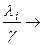к определенному пределу.

Введем понятие длины пути :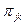

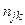= длина пути 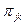- число каналов, входящих в путь .

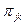Средняя длина пути

(1) 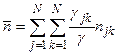- инвариантна по отношению к уровню трафика

(2)

тогда, подставляя (2) в (1), получим:

и

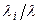- остается постоянным (не зависит от нагрузки на сеть g) и является функцией лишь процедуры выбора маршрутов.

Задача выбора пропускных способностей

Оптимальный (с точки зрания соотношения времени задержки и стоимости) выбор пропускных способностей из конечного набора их возможных значений.

Решается задача определения для сети с заданной топологией и известными потоками 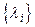. Необходимо, чтобы выполнялось ограничение

Рассматривается линейная функция стоимости: 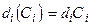, где - стоимость в расчете на единицу пропускной способности i -го канала. часто берется пропорциональным физической длине канала.

Задача

Составим функцию Лагранжа: (метод неопределенных множителей Лагранжа)

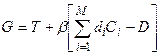
Составим систему M уравнений:

Найдем постоянную b:

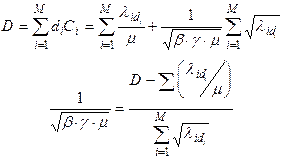
Определим добавочную стоимость как

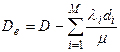
Тогда (набор пропускных способностей по закону )

каждый канал имеет пропускную способность по крайней мере и кроме того некоторую дополнительную пропускную способность. При этом минимальная средняя задержка в сети , пропускные способности каналов в которой выбраны оптимально:

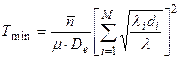
при 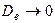средняя задержка пакета в сети неограниченно возрастает. Если , задача ВПС имеет реализуемое решение (т. е. ). Это условие является условием устойчивости.

Если 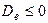, задача не имеет реализуемого решения.

При 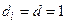- спутниковые каналы

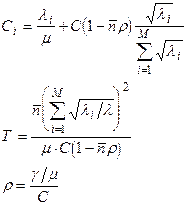
топологическую структуру сети следует выбирать так, чтобы получить минимальную среднюю задержку - полносвязная сеть.

в числителе минимизируется, когда одна из величин равна 1, остальные 0 - весь трафик направлен по одному каналу - вырожденный случай. Однако можно сделать вывод, что большую часть трафика нужно посылать по нескольким скоростным каналам и лишь малую часть по остальным каналам.

Обычно для связи требуются по крайней мере один входящий и один исходящий каналы для каждого узла. Такая сеть представляет собой кольцо. Но в этой сети средняя длина пути пропорциональна числу каналов M и зависит от распределения входящей нагрузки .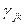

Другая сеть, в которой также имеется один входящий и один исходящий канал на каждый узел, за исключением центрального,- звездообразная. В этом случае достигается относительно высокая концентрация трафика на каждой линии и средняя длина пути .

Теперь следует сделать выбор между полносвязной сетью, звездообразной сетью и всеми сетями, промежуточной между ними. Клейнрок показал, что при 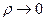наиболее подходящей является звездообразная сеть, а при 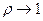- полносвязная сеть. Можно ожидать, что между этими двумя экстремумами приемлемую топологию дает добавление некоторых прямых каналов к звездообразной сети.

Полученные выше выводы относятся к фиксированным процедурам выбора маршрутов.

Дата добавления: 2014-01-04