Булевы функции

Для описания функционирования логических схем используются булевы функции.

Булевой функцией n переменных x ₁, x ₂, …, x_n называется функция вида f = j (x ₁, x ₂, …, x_n), где переменные x_i равны 0 или 1; и функция f равна 0 или 1; переменные объединены конечным числом булевых операций – отрицание, конъюнкция и дизъюнкция.

Область определения булевой функции n переменных – совокупность всевозможных n - мерных наборов, компонентами которых являются двоичные значения 0 и 1. Каждая компонента набора соответствует одной из переменных набора x ₁, x ₂, …, x_n. Функция n переменных определяется на N = 2 ⁿ наборах.

Булева функция может задаваться таблицей истинности. В таблице перечисляются всевозможные наборы, составляющие область определения функции, и для каждого набора указывается значение 0, 1 или d, которое имеет функция на этом наборе. Знак d отмечает неопределенное значение функции. На месте неопределенного значения d при необходимости можно указывать значение 0 или 1.

Несущественный набор – набор, на котором функция принимает неопределенное значение. Несущественные наборы появляются в том случае, если значение функции на наборе безразлично или если реально существующая область определения функции состоит из числа наборов, меньшего 2 ⁿ.

Полностью определенная функция – булева функция, определенная на всем множестве наборов.

Частично определенная функция – булева функция, содержащая несущественные наборы.

Старшинство булевых операций: отрицание, конъюнкция, дизъюнкция. Для изменения порядка выполнения действий используются скобки.

В табл. 1.1 представлены основные логические функции, математическое описание и реализация этих функций с помощью релейно-контактных и логических элементов.

Таблица 1.1. Основные логические функции

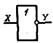
Логическая функция	Математическое описание	Контактная схема	Изображение элемента
НЕ (инвертор)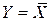
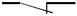
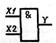
И (конъюнктор)	Y = X1X2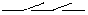
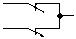
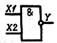
И – НЕ (штрих Шеффера)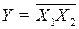
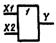
ИЛИ (дизъюнктор)	Y = X1+X2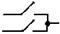
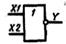
ИЛИ – НЕ (стрелка Пирса)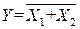

Описание логических функций в виде таблиц истинности приведено в табл. 1.2

Таблица 1.2. Таблицы истинности

НЕ	И; И – НЕ	ИЛИ; ИЛИ – НЕ
X	Y	X 2	X 1	Y		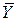X 2	X 1	Y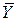

Дата добавления: 2014-01-04