Вероятность безотказной работы ЭА

Возникновение отказов в ЭА носит случайный характер. Следова­тельно, время безотказной работы есть случайная величина, для описания которой используют разные распределения: Вейбулла, экспоненциальный, Релея, Пуассона.

Отказы в ЭА, содержащей большое число однотипных неремонтируемых элементов, достаточно хорошо подчиняются распределению Вейбулла, а вероятность безотказной работы P(t), частота отказов f(t), средняя нара­ботка на отказ T_ср вычисляются по следующим формулам:

(4.10) (4.11) (4.12)

где Г — гамма-функция; λо и b — параметры распределения. Из (4.10) и (4.11) получим

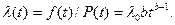
Пример. Время безотказной работы системы подчиняется закону Вейбулла с параметрами Ь = 1,5 и λо = 10^-4ч^-1. Определить параметры надежности системы за время работы t = 100 ч.

Решение:

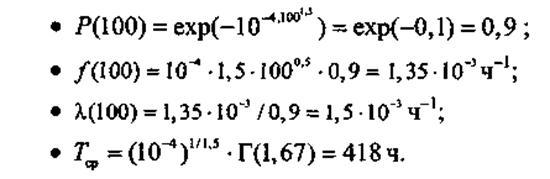
Экспоненциальное распределение (частный случай распределения Вейбулла при b = 1) основано на предположении постоянной во времени интенсивности отказов и успешно может быть использовано при расчетах надежности аппаратуры одноразового применения, содержащей большое число неремонтируемых компонентов.

Характеристики надежности при этом распределении выглядят сле­дующим образом:

где X — параметр распределения.

Пример. Время безотказной работы системы подчиняется экспоненциально­му закону с параметром λо= 10^-4ч^-1. Определить параметры надежности системы за время работы t = 100 ч.

P(100)=exp(-10^-4*100)=0.99

f(100)=10^-4*0.99=0.99*10^-4

Tcp=1/10^-4=10⁴ ч

При длительной работе ЭА при планировании ее ремонта важно знать не вероятность возникновения отказов, а их число за определенный период эксплуатации. В этом случае применяют распределение Пуассона, позво­ляющее подсчитать вероятность появления любого числа случайных собы­тий за некоторый период времени. При расчетах для распределения Пуассо­на характерны те же ограничения, что и для экспоненциального. Распреде­ление Пуассона применимо для оценки надежности ремонтируемой ЭА с простейшим потоком отказов.

Вероятность отсутствия отказа за время t составляет Р₀ = exp(-λt), a

вероятность появления i отказов за то же время P_i =λⁱtⁱ exp(-λt)/i!, где / i = 0,1,2,..., п — число отказов.

Пример. Вероятность безотказной работы ЭВМ с параметром X =10~³ч~' подчиняется закону Пуассона. Определить вероятность отсутствия отказа и появле­ния двух отказов в продолжении 1000 ч работы ЭВМ.

Решение:

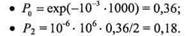
Распределение Релея описывает поведение ЭА и составляющих ее элементов с явно выраженными признаками их старения и износа. При этом

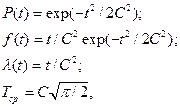
где С— параметр распределения.

Пример. Время безотказной работы ЭА подчиняется распределению Релея с па­раметром С= 500 ч. Определить параметры надежности ЭА за время работы t = 100 ч. Решение:

Дата добавления: 2014-01-04