Пример использования метода наименьших квадратов

В результате проведения опытов и фиксирования их результатов получены опытные данные, представленные в табл. 6.2. По этим данным необходимо получить эмпирическую формулу для описания функциональной зависимости y = f(x).

Если изобразить табличные данные на графике (см. рис. 6.3), легко убедиться, что в качестве эмпирической формулы для аппроксимации

Таблица 6.2

Таблица с опытными данными

xi	0,75	1,50	2,25	3,00	3,75
yiэ	2,50	1,20	1,12	2,25	4,28

Рис. 6.3. Расположение опытных данных, представленных в табл. 6.2,

на графике (еще например у3э и х3)

опытной функции можно принять параболу, т.е. квадратный трехчлен:

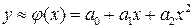. (6.19)

Формула для суммы квадратов отклонений имеет вид:

.

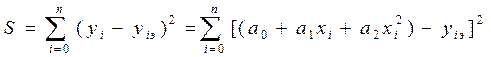В данном случае n = 4, m = 2. Найдем частные производные функции :

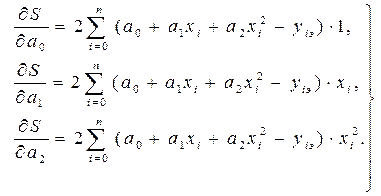
Приравнивая эти выражения 0 и собирая коэффициенты при неизвестных , получаем следующую систему линейных уравнений:

(6.20)

После подстановки числовых данных из табл. 6.2 система (6.20) запишется:

(6.21)

Систему (6.21) можно решить по правилу Крамера (методу определителей): а₀ = 5,54; а₁ = -4,73; а₂ = 1,19. Таким образом, получим следующую аппроксимацию функции, заданной в табличном виде:

. (6.22)

Оценим относительные погрешности полученной аппроксимации в заданных точках. Для этого найдем значения

,

где рассчитывается по формуле (6.22). Например:

Результаты вычислений сводим в табл. 6.3.

Таблица 6.3

Результаты оценки точности эмпирической формулы (6.22)

хi	yi	yiэ	εi	δyi
0,75	2,66	2,50	0,16	0,064
1,5	1,12	1,20	-0,08	-0,067
2,25	0,92	1,12	-0,20	-0,179
3,00	2,06	2,25	-0,19	-0,084
3,75	4,54	4,28	0,26	0,061

Вычислим среднюю квадратичную ошибку аппроксимации по формуле (6.18):

.

Примечание 1. При использовании линейной эмпирической формулы (6.4) система уравнений для расчета коэффициентов 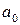и 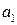имеет следующий вид:

(6.23)

Примечание 2. При использовании степенной эмпирической формулы (6.6) для приведения ее к линейному виду формулу прологарифмируем. Получим:

.

Обозначим , , , . В результате получим формулу

.

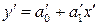Для определения коэффициентов и решают систему вида (6.23), подставляя в нее значения и . После расчета и вычисляют и .

При расчете ошибки аппроксимации 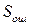по формуле (6.18) расчетные значения определяют по формуле (6.6) и в нее подставляют исходные (не логарифмированные) значения .

Дата добавления: 2014-01-04